AVL 樹是一種會自我平衡的二元搜尋樹(Binary Search Tree，見兩天前文章)，對每一個節點來說，左右兩邊的高度差(height difference)要小於等於1，如高度差大於1，節點會旋轉(rotate)直至樹平衡(balance)。
加入新節點後，依不平衡的狀況又分為LL(left-left condition)、LR(left-right condition)、RR(right-right condition)、RL(right-left condition)。這裡用圖加程式碼說明可能會比較容易理解:
首先來講left-left condition: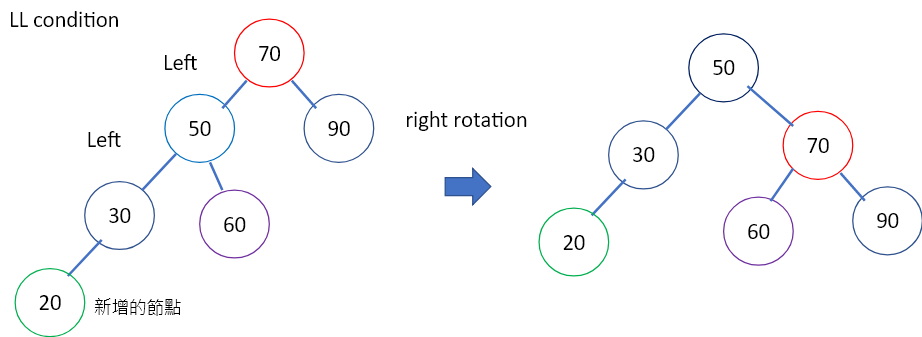

圖1.加入的新節點根據二元搜尋樹的規則，會在node30的left child，但這樣會造成node70不平衡(imbalance)(因為左側高度為3，右側高度為1，高度差為2。)因為不平衡點在左側，然後插入的節點也在左邊子樹的左側，故我們稱之為left-left condition或LL condition(直翻叫左左情況，聽起來有點過於俏皮，我們在本篇就使用LL代替)。此時我們要對離新增節點最近的不平衡點做右旋，也就是node70。node70的左邊先改接上node50 right child，node50的right child再接上node70。右旋寫作程式碼如下，可能會比看圖容易理解:

def right_rotate(node):
    new_root=node.leftchild
    node.leftchild=node.leftchild.rightchild
    new_root.rightchild=node

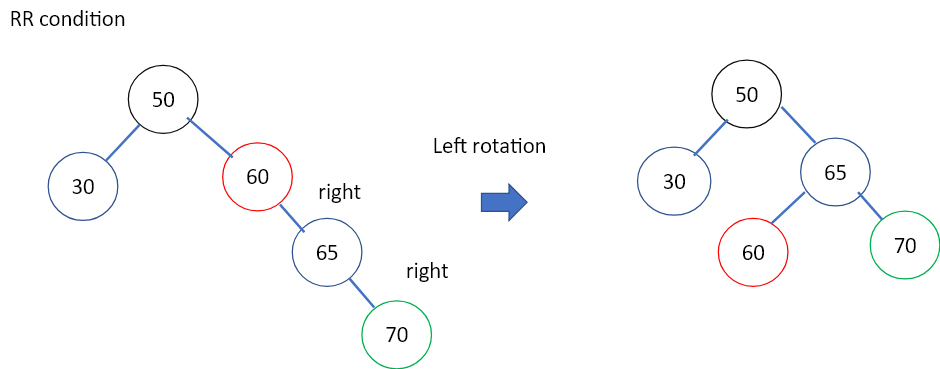
圖2.加入的新節點根據二元搜尋樹的規則，會在node65的right child，但這樣會造成node60不平衡(left.height=0, right.height=2,balance=2大於1)。由於不平衡點在右側，然後插入的節點也在不平衡點rightchild的右側(見圖)，故為right-right condition(or RR condition)。此時我們要對離新增節點最近的不平衡點做左旋，也就是node65。左旋寫作程式碼如下，和右旋差不多，左右相反而已:

def left_rotate(node):
    new_node=node.rightchild
    node.rightchild=node.rightchild.leftchild
    new_root.rightchild=node

接著我們來看LR condition: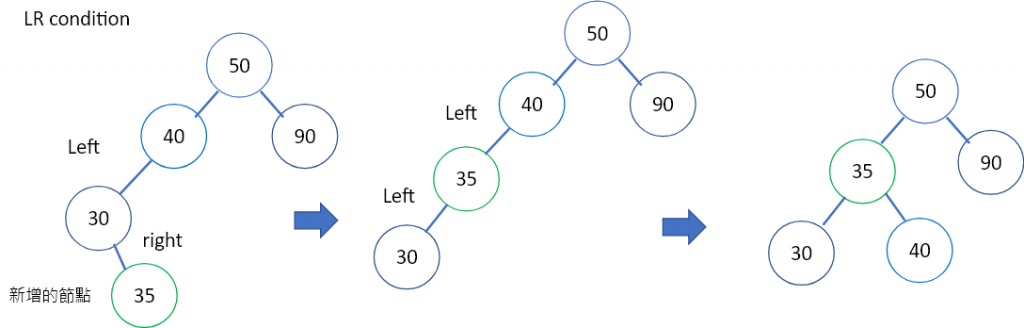

圖3.加入的新節點根據二元搜尋樹的規則，會在node30的right child，但這樣造成node40不平衡。由於新增節點在不平衡節點left child的右邊，故為left right condition (LR condition)。這種情況，我們要先對node30做左旋，讓這個不平衡變成LL condition，再對node40做右旋。

同理RL condition也是類似的方法: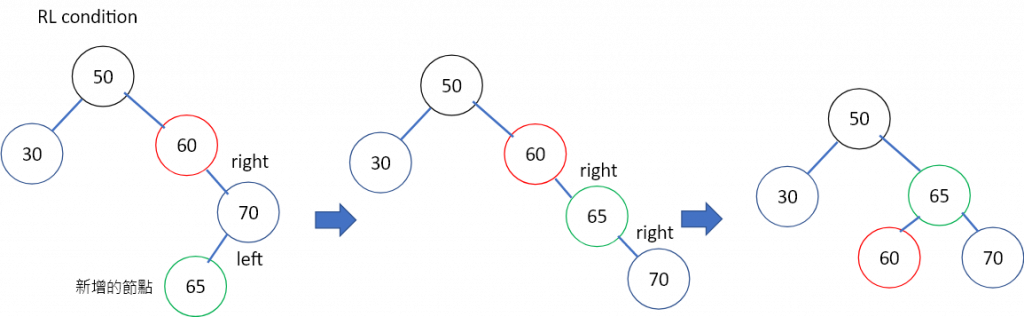

圖4.加入的新節點根據二元搜尋樹的規則，會在node70的left child，但這樣造成node60不平衡。由於新增節點在不平衡節點right child的左邊，故為right left condition (RL condition)。這種情況，我們要先對node70做左旋，讓這個不平衡變成LL condition，再對node60做右旋。
那下面我們就來看完整的程式碼吧~

# 一樣，因為我們要用level-order traversal來檢查我們的樹長怎麼樣了，所以還是import個deque module
from collections import deque
# for AVL tree 因為我們需要根據左右樹的高度差來判斷是否平衡，這裡我們給每個node多一個高度的屬性3
# time:O(1), space: O(1)
class TreeNode:
    def __init__(self, data=None):
        self.data = data
        self.leftchild = None
        self.rightchild = None
        self.height = 1
        
# 來個大家最熟悉的level-order traversal，用來檢查樹看起來怎麼樣了    
# time: O(n), space: O(n)
def levelordertraversal(rootNode):
    customqueue = deque()
    customqueue.append(rootNode)
    while len(customqueue) != 0:
        popped = customqueue.popleft()
        print(popped.data)
        if popped.leftchild is not None:
            customqueue.append(popped.leftchild)
        if popped.rightchild is not None:
            customqueue.append(popped.rightchild)
            
# 取得節點高度，為了避免在沒有節點的狀況(node==None)，程式出現error，這裡先定義好return 0 
# time:O(1), space: O(1)
def getHeight(node):
    if not node:
        return 0
    else:
        return node.height
        
# 先把計算高度差做成function，等等程式不至於看起來很雜亂
# time:O(1), space: O(1)
def getbalance(node):
    if not node:
        return node
    else:
        return getHeight(node.leftchild)-getHeight(node.rightchild)
        
# 右旋，旋轉後要重新計算高度，回傳新的root
# time:O(1), space: O(1)
def rightrotate(node):
    new_root = node.leftchild
    node.leftchild = node.leftchild.rightchild
    new_root.rightchild = node
    node.height = 1+max(getHeight(node.leftchild), getHeight(node.rightchild))
    new_root.height = 1+max(getHeight(new_root.leftchild),
                            getHeight(new_root.rightchild))
    return new_root

# 同理左旋
# time:O(1), space: O(1)
def leftrotate(node):
    new_root = node.rightchild
    node.rightchild = node.rightchild.leftchild
    new_root.leftchild = node
    node.height = 1+max(getHeight(node.leftchild), getHeight(node.rightchild))
    new_root.height = 1+max(getHeight(new_root.leftchild),
                            getHeight(new_root.rightchild))
    return new_root


# 插入節點: time:O(logn), space:O(logn)
def insertNode(rootNode, value):
    if rootNode is None:
        rootNode = TreeNode(value)
        return rootNode
    elif value < rootNode.data:
        rootNode.leftchild = insertNode(rootNode.leftchild, value)
    elif value > rootNode.data:
        rootNode.rightchild = insertNode(rootNode.rightchild, value)

    rootNode.height = 1+max(getHeight(rootNode.leftchild),
                            getHeight(rootNode.rightchild))
    balance = getHeight(rootNode.leftchild)-getHeight(rootNode.rightchild)
    # left-left condition
    if balance > 1 and value < rootNode.leftchild.data:
        return rightrotate(rootNode)
    # left-right condition
    elif balance > 1 and value > rootNode.leftchild.data:
        rootNode.leftchild = leftrotate(rootNode.leftchild)
        return rightrotate(rootNode)
    # right-right condition
    if balance < -1 and value > rootNode.rightchild.data:
        return leftrotate(rootNode)
    # right-left condition
    elif balance < -1 and value < rootNode.leftchild.data:
        rootNode.rightchild = rightrotate(rootNode.leftchild)
        return leftrotate(rootNode)
    return rootNode
    
# 跟Binary search tree一樣找local min，給delete node function準備的
def findlocalmin(node):
    current = node
    while current.leftchild is not None:
        current = current.leftchild
    return current

# 刪除節點，前面的部分和二元搜尋樹一樣，後面多了balance的部分，概念大同小異
# time:O(logn), space:O(logn)
def deleteNode(rootNode, value):
    if not rootNode:
        return rootNode
    elif value < rootNode.data:
        rootNode.leftchild = deleteNode(rootNode.leftchild, value)
    elif value > rootNode.data:
        rootNode.rightchild = deleteNode(rootNode.rightchild, value)
    else:
        if rootNode.rightchild is None:
            rootNode = rootNode.leftchild
            return rootNode
        elif rootNode.leftchild is None:
            rootNode = rootNode.rightchild
            return rootNode
        else:
            temp = findlocalmin(rootNode.rightchild)
            rootNode.data = temp.data
            rootNode.rightchild = deleteNode(rootNode.rightchild, temp.data)
    rootNode.height = 1+max(getHeight(rootNode.leftchild),
                            getHeight(rootNode.rightchild))
    balance = getbalance(rootNode)
    # again we have to balance the tree
    # LL condition
    if balance > 1 and getbalance(rootNode.leftchild) > 0:
        return rightrotate(rootNode)
    # LR condtion
    elif balance > 1 and getbalance(rootNode.leftchild) < 0:
        rootNode.leftchild = leftrotate(rootNode.leftchild)
        return rightrotate(rootNode)
    # RR condition
    elif balance < -1 and getbalance(rootNode.rightchild) < 0:
        return leftrotate(rootNode)
    # RL condition
    elif balance < -1 and getbalance(rootNode.rightchild) > 0:
        rootNode.rightchild = rightrotate(rootNode.rightchild)
        return leftrotate(rootNode)
    else:
        return rootNode

讓我們直接測試看看吧!

AVL = TreeNode(50)
AVL = insertNode(AVL, 30)
AVL = insertNode(AVL, 60)
AVL = insertNode(AVL, 65)
AVL = insertNode(AVL, 70)
levelordertraversal(AVL)
>>  50
    30
    65
    60
    70
AVL = deleteNode(AVL, 30)
levelordertraversal(AVL)
>>  50
    65
    60
    70

參考資料:
這篇寫得真的不錯，寫得蠻清楚的:
https://josephjsf2.github.io/data/structure/and/algorithm/2019/06/22/avl-tree.html
The Complete Data Structures and Algorithms Course in Python (Udemy)