二元堆積(Binary Heap)為一有以下性質的二元樹:
1. 所有的parent nodes必須比下面的children nodes值都小(min heap)或都大(max heap)。也就是說，如果是min heap，root會是整個tree的最小值；如果是max heap，root會是整個tree的最大值。
2. 是個complete tree(除了最後一層外每一層皆被填滿)。因此，array/list適合用來表現binary heap。

這樣的性質，使得如果我們要找最大或最小值或是插入額外的數值，時間複雜度能大大的降低。(如圖1)實際使用的例子包含: Prim’s Algorithm, Heap Sort or Priority Queue。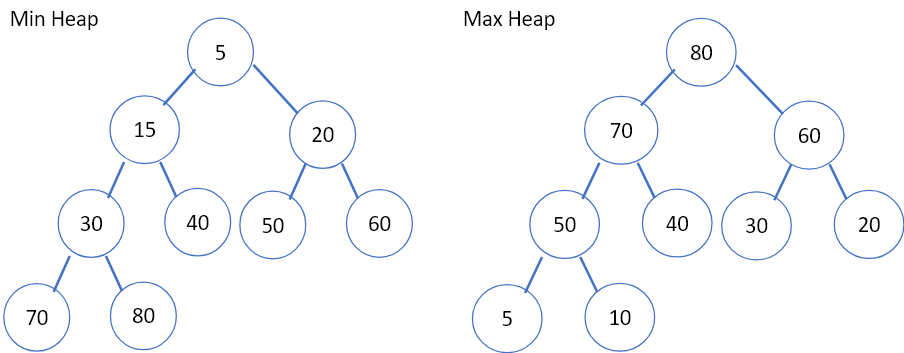

圖1. 左:為Min Heap，可以看到root以下的所有子孫都比自己大。所有parent都比自己的children小。右: 為Max Heap，所有children都比自己的parent小。

# 用python list建一個有限大小的Binary Heap，一樣因為index=0 不用，我們這裡寫作maxsize+1
# Time: O(1), Space: O(n)
class BinaryHeap:
    def __init__(self, maxsize, heaptype):
        self.customList = [None]*(maxsize+1)
        self.maxsize = maxsize
        self.heapsize = 0
        self.heaptype = heaptype
    # print function 其實跟level order traversal 一樣
# 讓他可以直接print出level order traversal的結果，用來檢查用
# time o(n), space: o(1)
    def __str__(self):
        if self.heapsize == 0:
            return
        else:
            res = ''
            for i in range(1, self.heapsize+1):
                res += str(self.customList[i])
                res += ' '
            return res
            
# 先定義幾個function等等在寫的時候不至於很雜亂
def swap(customList, index1, index2):
    customList[index1], customList[index2] = customList[index2], customList[index1]
    return customList
    
# 在heap中插入節點，先插在最末端，然後再用heapifyinsertNode去調
# time:log(n), space:log(n)
def insertNode(rootNode, value):
    if rootNode.heapsize >= rootNode.maxsize:
        return 'The heap is full...'
    else:
        rootNode.heapsize += 1
        rootNode.customList[rootNode.heapsize] = value
        heapifyinsertNode(rootNode, rootNode.heapsize)

# 調整插入節點的位子，不斷跟parent node比較，始之符合binary heap的規則
def heapifyinsertNode(rootNode, index):
    if not rootNode or index < 2:
        return
    parent = index//2
    if rootNode.heaptype == 'Min':
        if rootNode.customList[parent] > rootNode.customList[index]:
            rootNode.customList = swap(rootNode.customList, parent, index)
            heapifyinsertNode(rootNode, parent)
        else:
            return
    elif rootNode.heaptype == 'Max':
        if rootNode.customList[parent] < rootNode.customList[index]:
            rootNode.customList = swap(rootNode.customList, parent, index)
            heapifyinsertNode(rootNode, parent)
        else:
            return
#　根據index刪除節點，刪除的節點先用最末端節點取代，然後再用heapifydeleteNode跟後面節點調整位子
#　time: O(logn), space: O(logn)
def deletebyindex(rootNode, index):
    if rootNode.heapsize == 0:
        return 'The heap is empty...'
    else:
        rootNode.customList[index] = rootNode.customList[rootNode.heapsize]
        rootNode.customList[rootNode.heapsize] = None
        rootNode.heapsize -= 1
        heapifydeleteNode(rootNode, index)
        
# 再取代欲刪除節點後，調整節點的位子
# time:O(logn), space: O(logn)
def heapifydeleteNode(rootNode, index):
    leftchild = 2*index
    rightchild = 2*index+1
    swapchild = 0
    if leftchild > rootNode.heapsize:
        return
    # if there's only one child for the node
    elif leftchild == rootNode.heapsize:
        rootNode.customList = swap(rootNode.customList, index, leftchild)
    # if it has both children
    else:
        if rootNode.heaptype == 'Min':
            if rootNode.customList[leftchild] < rootNode.customList[rightchild]:
                swapchild = leftchild
            else:
                swapchild = rightchild
        else:
            if rootNode.customList[leftchild] > rootNode.customList[rightchild]:
                swapchild = leftchild
            else:
                swapchild = rightchild

        rootNode.customList = swap(rootNode.customList, index, swapchild)
        heapifydeleteNode(rootNode, swapchild)
  
# 取得節點的index，可以用在以value為基準刪除節點的時候
# time:O(n), space: O(1)
def getindex(rootNode, value):
    if rootNode.heapsize == 0:
        return
    else:
        for i in range(1, rootNode.heapsize+1):
            if rootNode.customList[i] == value:
                return i

# 根據value刪除節點
# time: O(n), space:O(logn) 主要是因為多了一個找value回傳index的動作
def deleteNode(rootNode, value):
    if rootNode.heapsize == 0:
        return 'The heap is empty...'
    else:
        index = getindex(rootNode, value)
        rootNode.customList[index] = rootNode.customList[rootNode.heapsize]
        rootNode.customList[rootNode.heapsize] = None
        rootNode.heapsize -= 1
        heapifydeleteNode(rootNode, index)
# 刪除整個binary heap
# time:O(1) space:O(1)
def deleteall(rootNode):
    rootNode.customList = None
    rootNode.maxsize = 0
    rootNode.heapsize = 0
    return 'Successfully delete the heap!'

直接來試試:

BH = BinaryHeap(10, 'Min')
insertNode(BH, 5)
insertNode(BH, 90)
insertNode(BH, 50)
insertNode(BH, 60)
insertNode(BH, 2)
print('== before deletion ==')
print(BH)
print('===after deletion===')
deletebyindex(BH, 1)
print(BH)
>>  == before deletion ==
    2 5 50 90 60 
    ===after deletion===
    5 90 50 60 

剛發完文發現~今天應該是AVL Tree，那明天再來看AVL Tree吧 ~

參考資料:
The Complete Data Structures and Algorithms Course in Python (udemy)