在訓練神經網絡時，最常用的算法是反向傳播（back propagation）。在這個算法中，根據損失函數對給定參數的梯度，調整參數（模型權重）。

為了計算這些梯度，PyTorch內置了一個稱為torch.autograd的微分引擎。它支援對於任何計算圖的自動梯度計算，我們用一個簡單的單層神經網絡為例，如下圖：

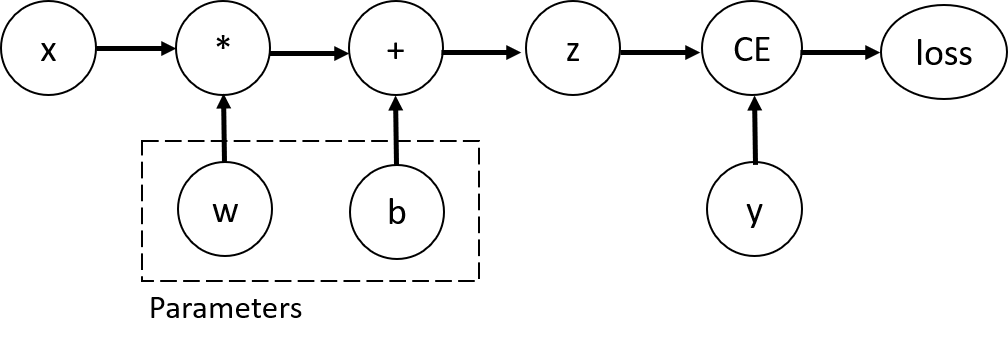
此網路具有輸入x、參數w和b，以及一個損失函數。可以使用以下方式在PyTorch中定義它：

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

在這個網絡中，w和b是需要優化的參數。因此，我們需要能夠計算損失函數對這些變數的梯度。因此將 w 和 b 張量的requires_grad屬性設為 True。這樣一來，PyTorch會紀錄這些張量的計算過程，因此可以使用反向傳播法計算梯度來優化參數。

我們對張量應用的用於構建計算圖的函數實際上是 Function類別。正向傳播過程中計算函數，並且在反向傳播步驟中也知道如何計算其導數。對於一個張量，它的反向傳播函數的引用被存儲在grad_fn屬性中，透過以下程式碼來顯示此屬性：

print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

為了優化神經網絡中的參數權重，我們需要計算損失函數相對於參數的導數，這邊使用偏微分的方法（放心我們知道大概在幹嘛就好，交給機器幫我們做數學運算），我們調用loss.backward()，然後顯示w.grad和b.grad的值：

loss.backward()
print(w.grad)
print(b.grad)

預設情況下，所有張量requires_grad=True都會追蹤其計算過程並支援梯度計算，但我們有時候不一定要更新參數，例如我們已經訓練好一個不錯的模型，要輸入資料來做預測，那麼模型就不需要更新參數，我們可以用 torch.no_grad() 來讓神經網路不更新：

z = torch.matmul(x, w)+b
print(z.requires_grad)

with torch.no_grad():
    z = torch.matmul(x, w)+b
print(z.requires_grad)

結語

今天介紹如何通過 Pytorch 來幫我們做反向傳播法，這也是我們為什麼要使用框架的原因，我們可以理解網路怎麼運做的，但不用實際去計算複雜的算術過程。