作者介紹

Erdős–Rényi（ER） model 是一種基本的數學模型，並且在 1959 由兩位匈牙利的數學家 Paul Erdős 跟 Alfréd Rényi 發表出來。主要是用來生成 Random Graph，生成圖的原因很簡單，就是用來模擬/研究現實生活中資訊傳播的運作以及影響。其中，ER Model 又是最簡單、易懂的數學模型之一。因為在模型裡只使用到了兩個參數，分別是 p 任兩節點之間的連接機率；n 為節點的數量，研究人員可以用很簡單方式去產生各式各樣的圖，去模擬資訊傳播的過程。

模型定義

• 任選兩節點最多可連接成邊的數量為：
• 任兩個節點產生邊的機率為：
• 邊的期望值為：

Binomial vs. Poisson Degree Distribution

ER Model 的分布為 Binomial Distribution 或是 Poisson Distribution，但是這兩種 Distribution 所使用到的參數不太一樣，Bionominal Distribution 同時使用到 n 跟 k；Poisson Distribution 只有使用到 k 也就是預期產生多少條邊，也因為 Poisson Distribution 計算上比較簡單所以比較受歡迎。

• Binomial Distribution 的公式：
• Poisson Distribution：

超簡單實作 + 視覺化

直接使用 networkx 來生成圖以及使用 gravis 來做視覺化。

安裝 networkx & gravis

pip install networkx gravis

import networkx as nx
import gravis as gv

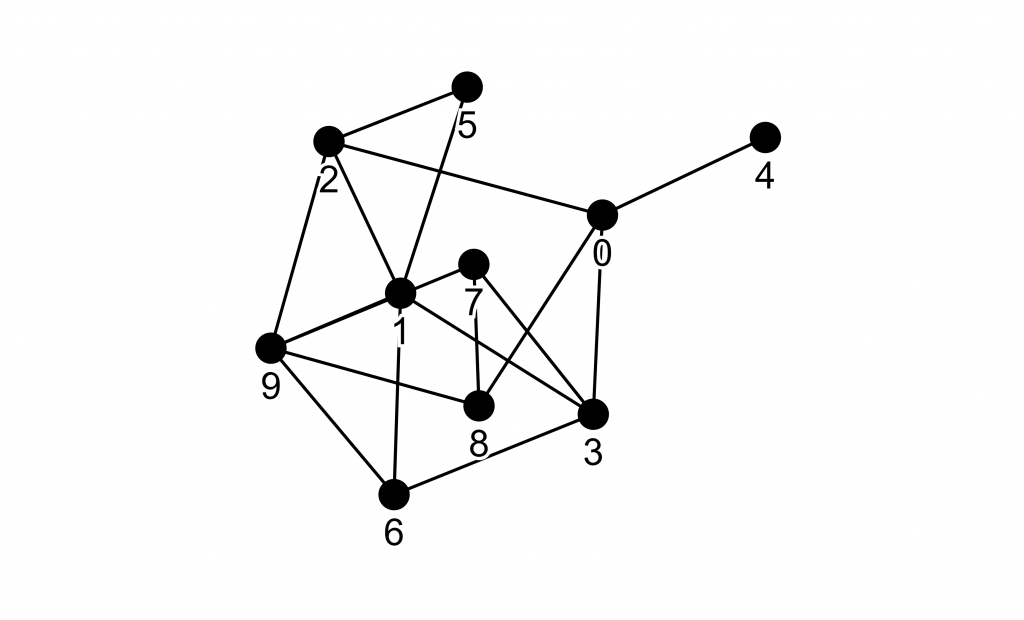
G = nx.gnp_random_graph(n=10, p=0.3, seed=42)
gv.d3(G)

然後就會產生像是下面的圖。

參考資料

• Network Science
• Erdős–Rényi model