「浮點數表示法」是電腦表示「實數」最常用的方式,類似十進位的科學記號表示法,目前所採用的「浮點數表示法」都是以 IEEE745 為運算標準
之所以稱為「浮點數表示法」,是因其小數點是浮動的,在有限位元的情況下,我們所能表示的數值範圍比起固定小數點(定點數)還要大以及彈性許多,依位元數可以分為「半精度浮點數」、「單精度浮點數」、「雙精度浮點數」,IEEE 754 將浮點數值分成以下三部份組成:
「指數」和「尾數」的位元數依照不同浮點數表示法而有所不同,這裡用表格來呈現:
浮點數表示法 | 符號(S) | 指數(E) |尾數(F)
------------- | -------------
半精度浮點數 | 1 位元 | 5 位元 | 10 位元
單精度浮點數 | 1 位元 | 8 位元 | 23 位元
雙精度浮點數| 1 位元 | 11 位元 | 52 位元
介紹了浮點數表示法的組成部分後,這裡附上一個將「實數」轉換成「浮點數」的計算公式:
如果你看不懂這公式,先別緊張!!也不需要特別背它
透過例子(後面會有)熟悉轉換流程,後面自然就可以慢慢理解公式
[補充]
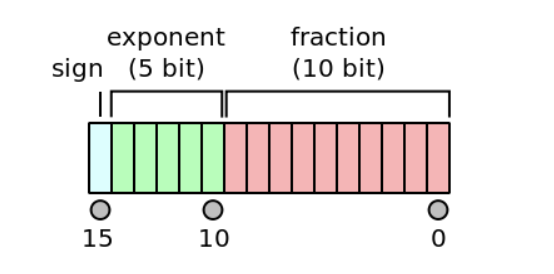
總共有 16 位元,只適合存儲對精度要求不高的數字,不適合用來計算。與單精度浮點數相比,優點是只需要一半的存儲空間,但是就犧牲了精準度和數值範圍
也可以叫「單倍精準數」,總共有 32 個位元,是 C 語言中的 float 型態,若要將數值轉換為 IEEE745「單精度浮點數」的步驟如下:
STEP1: 如果是「正數」,S = 0; 如果是「負數」,S = 1
STEP2: 將數值轉換為「二進位」表示,可以分為「整數部分」和「小數部分」。你可以先理解為「整數部分」是不斷地除以 2 ,「小數部分」則是不斷地乘以 2 。之後再把整數和小數的結果合在一起
STEP3: 將 STEP2 的結果變成 1.F 的形式, E(指數)的部份 = 小數點移動的 X 位(偏移量) + 127(加上127是以 Excess127(過剩127)方式表示),並把結果轉換為二進位
STEP4: 填入「尾數」的小數點數值
講了那麼多,直接來看例子吧 ![]() ,為了易讀,每四個 bit 就會用底線(_)區隔開來
,為了易讀,每四個 bit 就會用底線(_)區隔開來
範例一:將 -11.3 轉為「單精度浮點數」,數值為多少?
STEP1: 因為是負數,所以 S(符號) = 1
STEP2: 11.3 的「整數部分」是「11」轉換為二進位為 1011 ,「小數部分」是「0.3」轉換為二進位為 0.0100_1100_1100...,後面數值都是 1100 ,所以用 ... 省略,將「整數部分」和「小數部分」合起來就是 1011.0100_1100_1100...
STEP3: 將1011.0100_1100_1100... 變成 1.F的形式,結果為 1.011_0100_1100_1100...,由於小數點右移了3位,所以可以得到 E(指數) = 3 + 127 = 130 ,轉換為二進位為 1000_0010
STEP4: F(尾數)就是「剩下的小數點部分」 ,F = 0110_1001_1001_1000...
合併幾來如下圖所示:

也可以叫「雙倍精準數」,總共有 64 個位元,是 C 語言中的 double 型態,計算步驟跟「單精度浮點數」差不多,比較需要注意的是「指數」和「尾數」的佔用位元數不同
javaScript 是弱型別,對於數值的處理,不論是整數或是有小數,都只有一種型別,那就是 Number,而且 是以 64 位元的雙精浮點數來計算,但浮點數的尾數(Fraction, F)因為位元數有限,如果超過的話,數值資料就會通通遺失,其計算後的結果值就會有尾數誤差,有些人把這個結果稱為浮點數的陷阱
「浮點數表示法」都是以 IEEE745 為運算標準,由「符號(S)」、「指數(E)」、「尾數(F)」組成。依照總位元數可以分為「半精度」、「單精度」、「雙精度」浮點數,總位元數越多的浮點數,所表示的數值範圍就可以越大,計算也相對精準。但浮點數的尾數(Fraction, F)因為位元數有限,如果超過的話,數值資料就會遺失,其計算後的結果值就會有誤差,這也是浮點數會損失精確度的原因
線上轉換器
