這篇也要來繼續算數學！！
如果要考研究所或是計概相關考試 可說是必考題
今天就稍微淺談一下電腦「如何表示整數」，什麼是「一補數」和「二補數」

數值資料

數值資料主要可以分為「整數」和「浮點數」，這篇要來談整數的部分，浮點數會在 Day 10 提到。電腦內部是個充滿「0」、「1」的世界，使用二進位數來表示。但是這樣的二進位數字都只是「無正負符號的整數」（unsigned interger）, 電腦內部並沒有 "+"、"-" 等符號來表示正、負數, 也沒有表示小數點的符號。所以，為了解決這些問題，就有幾種不同的負數與浮點數表示方法

整數表示法

「無正負符號的整數」

圖片取自台大-數位資料表示法

可以直接看上面的圖，「無正負符號的整數」會是以 8 個位元所表示。最小的位元字串會是 8 個 0 組成(00000000)，如果有 n 個位元，就可以表示 2 ^ n 個數，所表示的整數範圍是 0 ~ (2 ^ n) -1 之間。
例如使用 8 個位元，就可以表示 256 個數，所表示的整數範圍是 0 ~ 255 之間

「帶正負符號的整數」

圖片取自台大-數位資料表示法

以最左邊的位元來表示符號，像是 "+" 或 "-" ，0 表示此為正數; 1 表示此為負數，那麼剩下的 n-1 個位元則用來表示正負符號外的數值大小。
負數所表示的範圍是 0 ~ -(2 ^ n-1) -1; 正數所表示的範圍是 0 ~ (2 ^ n-1) -1 ，所以使用 8 個位元可以得到 -127 ~ 127 間的所有整數
但他會有個問題，就是會有兩個0（+0 和 -0），所以目前電腦不採用這種方式表示整數

補數表示法

補數的用意是為了用加法的方式來進行減法的運算

如果此二進位數值超過 n - 1 個位元，稱為「溢位」(overflow)，無法進行轉換

補數表示法可以分為：

• 一補數表示法
• 二補數表示法（當今電腦表示整數所使用的方法）

一補數(One's complement)

一補數表示法比較單純一點
「正數」的表示方式和前面提到的「帶正負符號的整數」一樣，而負數的表示法會有點不同。「負數」的表示會將二進位數的每個數字做反轉，0 轉成 1，1 轉成 0，轉換後得到的數就稱為原二進位的一補數
以下來看兩個例子：

例一：41 的一補數表示法為何？
STEP 1: 先將 41 轉為二進位數值 101001
STEP 2: 在二進位數值左邊補上0，直到有8個位元為止，因為是正數，所以最左邊為0，結果為 00101001

例二：-41 的一補數表示法為何？
STEP 1: 先將 41 轉為二進位數值 101001
STEP 2: 在二進位數值左邊補上0，直到有8個位元為止，結果為 00101001
STEP 3: 因為是負數，所以要把所有原為 0 的數轉為 1，原為 1 的數轉為 0 ，結果為 11010110

總結以上步驟，就是先把數值轉換為「二進位」，將二進位的數值左邊補上0 ，直到有 8 個位元為止，如果是「正數」，最左邊位元的數值 = 0。如果是「負數」，就要把原本為 0 的數轉為 1，原本為 1 的數轉為 0 ，並且要卻表最左邊的數值要 = 1

然而，一補數中會出現「兩個0」的問題，像是 00000000 和 11111111 都代表 0，這會造成計算上的混淆，以及他的加減法不是那麼直接，所以並未像二補數一樣被廣泛應用

二補數(Two's complement)

目前電腦儲存整數的方式是使用「二補數」
以下一樣來看兩個例子：

例一：40 的二補數表示法為何？
STEP 1: 先將 41 轉為二進位數值 101000
STEP 2: 在二進位數值左邊補上0，直到有8個位元為止，因為是正數，所以最左邊為0，結果為 00101000

例二：-40 的二補數表示法為何？
STEP 1: 先將 41 轉為二進位數值 101000
STEP 2: 在二進位數值左邊補上0，直到有8個位元為止，結果為 00101000
STEP 3: 因為是負數，所以要把最右邊的那些 0 和 最右邊的第一個 1 保持不變，並將其餘的位元中， 0 的數轉為 1， 1 的數轉為 0 ，結果為 11011000

總結來說，二補數的表示法一樣以最左邊的位元來表示正負，0 表示此為正數; 1 表示此為負數，那麼剩下的 n-1 個位元則用來表示數值大小。負數所表示的範圍是 -1 ~ -(2 ^ n-1) -1; 正數所表示的範圍是 0 ~ (2 ^ n-1) -1 ，所以使用 8 個位元可以得到 -128 ~ 127 間的所有整數。它只會有一個0 (就是00000000)，完美解決了「一補數」的問題，所以廣為目前電腦所採用的儲存方式～

總結

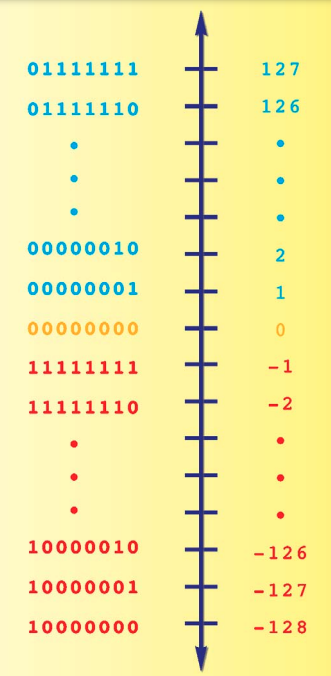
第一次接觸補數表示法需要花點時間熟悉，正數的「一補數」和「二補數」都蠻單純的，規則都一樣
但是負數的表示就不一樣啦！！ 可以透過例子和圖像去學習是比較快的方式(或是痛苦指數比較低?

參考資料

1. 關於補數與二進位運算
2. 台大-數位資料表示法
3. wikipedia

PS. 若有解說不清或是不正確之處，歡迎指教