
在擬定文章大綱之初,就在想今天這篇到底要怎麼寫比較好呢
回想自己當初在學習進位法互換的時候,是邊看書上的例子邊拿著紙和筆在旁邊算
為了避免長篇大論,這篇會以例子的方式來探討「十進位」和「二進位」的互換
如果你對進位法還不是很了解,可以參考之前的文章電腦的魔法語言 - 探索二進制世界的奧秘
前情提要:「十進位數」是指以基數 10 的運算系統,超過十就進位,其中包含了正數和零,但不包括負數,在計算機概論和程式設計中,表示負數的方式通常是使用二補數(Two's Complement)表示法。
你可能會在其他地方看到以下的表示方式,這是為了避免混淆,所以會在數值的右下方註明「基數」,十進位的數要不要註明都可以,下圖就是十進位轉二進位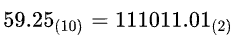
接下來討論幾個範例
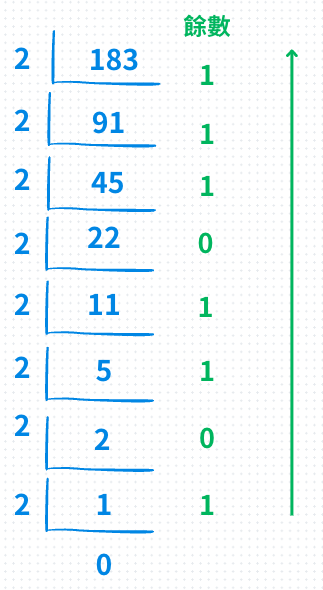
STEP1 : 先將 183 ÷ 2 = 91...1
STEP2 : 接著再把 91 ÷ 2 = 45...1
STEP3 : 以此類推...,直到除到不能再除為止
答案是 10110111
我們只要注意餘數的部分就好,最後要把所有餘數「由下到上」組合起來才會是最終結果,之所以「由下到上」,是因為每 「÷2」 次方數就會「遞增」,所以越後面除出來的餘數,為越高位
小數點的狀況比較多變,小數點中的整數部分最大為「1」,且還有可能會遇到「循環小數」,之後會透過範例二來說明

STEP1 : 先將 0.8125 x 2 = 1.6250,整數位為「1」
STEP2 : 接著再把 1.6250 的整數 1 扣掉 = 0.6250 再 x 2 = 1.2500,整數位為「1」
STEP3 : 接著再把 1.2500 的整數 1 扣掉 = 0.2500 再 x 2 = 0.5000,整數位為「0」
STEP4 : 最後把 0.5000 x 2 = 1.0000,整數位為「1」,這時候就不需要再扣1了,因為扣一就等於 0,怎麼乘r結果都是 0 ,沒有意義
答案是 0.1101
此範例中,要注意的是小數點的整數位如果有出現「1」,下一輪要記得扣掉「1」!!!,之所以要扣掉,可以理解為那是超過小數點的整數,如果不扣一繼續 X2,到後面就會超過範圍。所以只需要將扣掉後的剩餘小數繼續做運算即可。
最後再把所有整數位「由上到下」組合起來,之所以「由上到下」,是因為每 「X2」 次方數就會「遞減」,所以 2 ^ 0 會從最下面開始

0.01001100...,由於後面都是1100 再重複,所以就省略不計~ 這題是標準的「循環小數」的例子,有興趣的人可以試試看 0.1, 0.2 轉二進位,都會碰到這個囧況喔!在有限位數的二進位表示法下,永遠無法精確表示十進位的 0.3,但不用擔心,如果需要更精確的表示,可以使用「浮點數表示法」來縮小誤差
10110101.1101 轉換為十進位
STEP1: 整數部分為 10110101,由右到左分別是 2 ^ 0 ~ 2 ^ 7,所以就是 1 * (2 ^ 0) + 0 * (2 ^ 1) + 1 * (2 ^ 2) + 0 * (2 ^ 3)...以此類推,最後把所有的結果加總 = 181
STEP2: 小數部分為 0.1101,小數點左邊可以不用理會,專注處理右邊就好(也就是 1101 ),由左到右分別是 2 ^ -1 ~ 2 ^ -4,所以就是 1 * (2 ^ -1) + 1 * (2 ^ -2) + 0 * (2 ^ -3) + 1 * (2 ^ -4),,最後把所有的結果加總 = 0.5 + 0.25 + 0.0625 = 0.8125
STEP3: 最後再把「整數部分」和「小數部分」合併起來,得到的答案就是 181.8125
PS 可以自己出題目,自己對答案😆
https://tools.yeecord.com/calculator/dec/bin
(是說有轉換器,為何還要自己算呢![]()
二進位是所有進位法的地基,但不論是哪種進位,要表示的總數其實都是一樣的,只是表示方式不同而已。透過例子學習是比較快的方式,希望今天的內容能對你有所幫助~部分圖片因版面關係,所以省略掉了一些計算
