從 keras 框架運作一路看過來，機器在做學習會有個核心概念，這邊會展現出來讓前後關聯可以串通。

機器學習和很多著名的預測方法如貝氏理論、德爾菲法論等等，都有個非常非常相似的精神，即反覆執行 "修正" 的動作。之後會探討如貝氏理論的概念運作。

下圖為深度學習核心運作示意圖: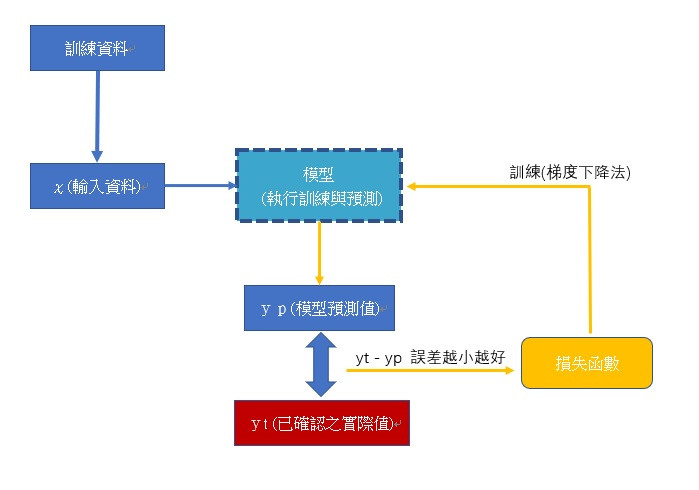

此為模型接收資料並迭代訓練示意圖。模型設定建構好後，將輸入資料載入模型內，模型做predict後會產生 yp 預測值，會透過與 yt 實際正確值做誤差計算與使用指定的損失函數，透過梯度下降法計算新的權重後，更新回模型中，再繼續以輸入資料重新預測、與實際正確值作誤差計算、透過損失函數更新模型權重。

重複訓練至設定的條件停止，或者參數判斷要於某個觀察點最大值或最小值，也就是最佳的模型狀態結束。

損失函數的選擇，其實就是在選擇適當的數學公式，這部分要實際試過，觀察其 loss value 有沒有降下來，降得越多，表示誤差越小越接近。

損失函數透過微分後可以觀察斜率，當斜率為0時，表示在此刻是一個低點，反之如果斜率在某時刻還是很大，也意味著其損失值還是非常大，需要繼續訓練讓斜率越來越小。 keras 可以透過 tensorflow.GradientTape 來達成梯度計算，可以查詢技術文件取得用法，這邊不繼續詳述。

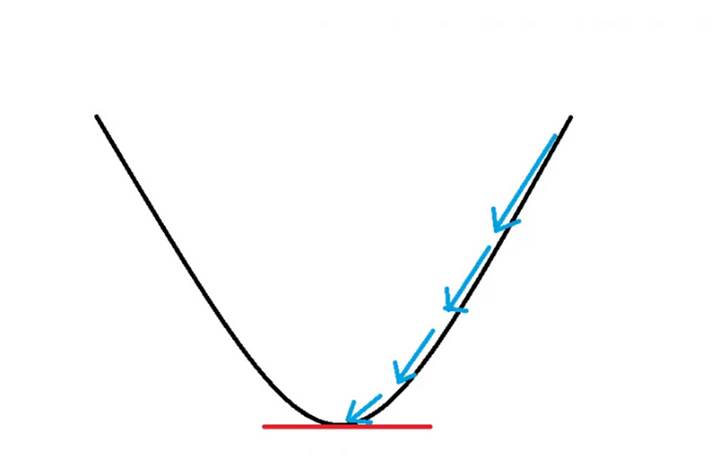
上圖將藍色箭頭，當作是權重向量要更新的方向，最後更新到損失函數最低點就是最佳、誤差最小的地方。

另一層涵義是，找損失函數，要找會讓計算的值是往收斂的方向，如果怎麼計算都降不下來，數據會發散而不是朝向收斂，就要考慮更換損失函數，或者減少神經網路的層數等等。

假設權重為向量(keras內為張量)，每次訓練都要往下降才能讓損失降為最小，所以每次都去減損失的值，這個損失值會乘上一個學習率，也就是在 optimizer with learning_rate 章節所提到的設定。下圖以2維權重向量示意: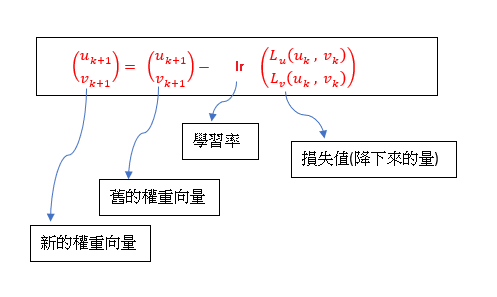

提到 keras 的 optimizer ， 這邊會有一種狀況，就是會有 過擬合(overfitting) 與 欠擬合(underfitting) 的狀況。 也就是在權重向量降下來時，到了一個區域相對低點就停下來了，也就是下圖右上方斜率為0處，而真正的低點是左下方並未偵測到。

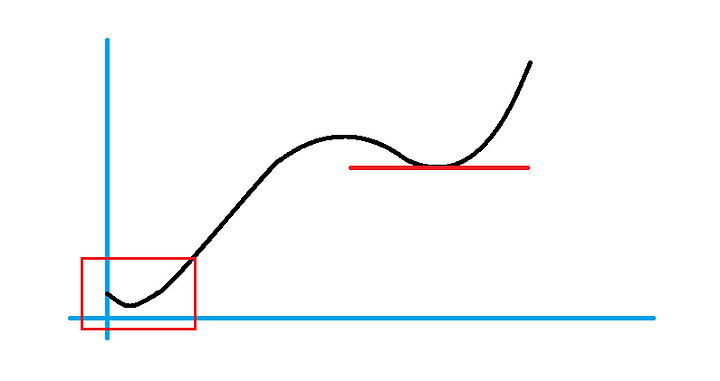
所以需要最佳化搜尋，也就是 keras 的 optimizer 在設定使用哪一種最佳化模組來避免這些狀況發生。其損失函式也可能極度不規則，以下引用維基百科所提供的3D圖示: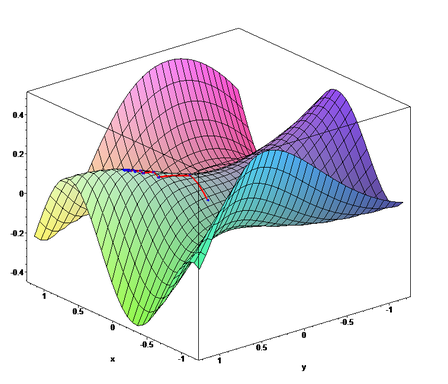

透過模型在做 compiler時，指定適當的 optimizer 可以減少誤判的機會。