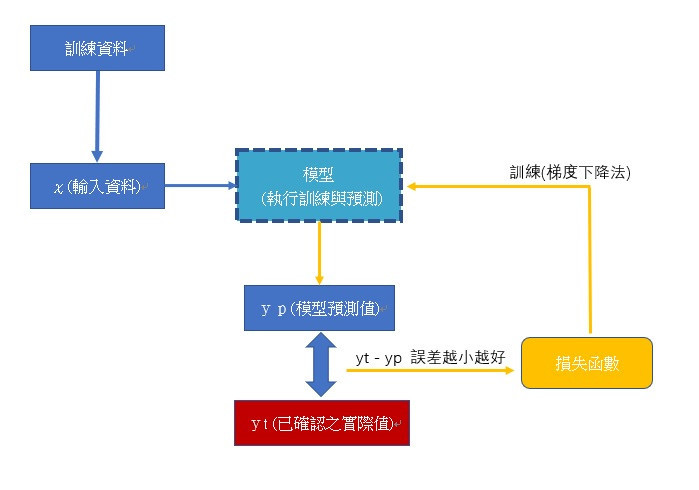
將概念擺在這個位置的目的，就是希望能夠呼應建構keras模型時的運作，並於自己呼叫keras API 時，知道自己在做什麼。 當概念在腦海裡，搭配前面的章節，就不會只是餵參數，而是真正能夠靈活又彈性地操作keras。

概念擺在此位置另一個目的是，比較不會被枯燥的理論澆熄了認識類神經網路的動機。就算如果不巧真的於此被澆熄了學習概念的意願，至少還保留了操作建構模型的技能，運氣好還是能夠建出好的模型。但有概念會在這塊領域更加如魚得水。

Pre-knowledge

1.Exponential function

2.Euler’s numbers

3.Sigmoid

4.Gradient Descent 梯度下降

Logistic Regression Classification

梯度下降法的重點在於建立可微的損失函數，最終逐步找出使損失函數最小的參數，從而產生預測函數進行預測。

但如果應用於分類問題（是否改進、是否安全、是否可用等），僅靠預測值不足以區分它是哪一類。

要留意以下觀點:
(1)預計預測值的大小可以從負無窮大到正無窮大，無法實現分類。我們希望預期分類為 0 或 1。
也就是說，目標為 0 或 1。

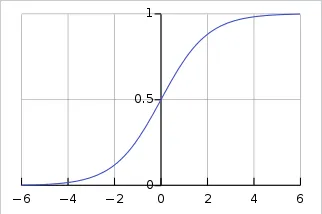
(2)我們能不能想辦法把數值縮小到0到1之間

(3) 綜合(1)、(2)點，Sigmoid函數可以做到

轉換為0到1之間的值也可以視為代表機率！機率接近0或接近1！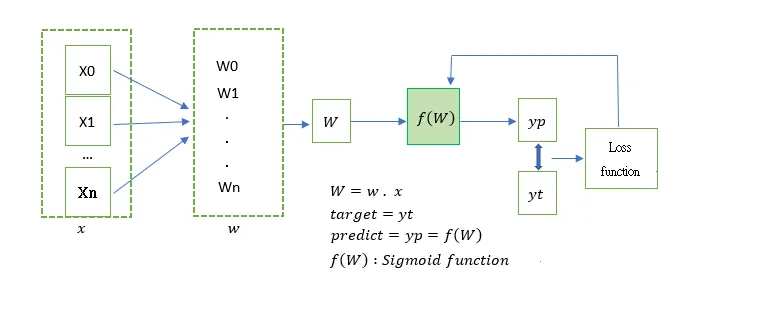

損失函數（交叉熵）

模型預測階段行為表示：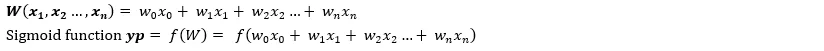

yt只能是 0 或 1 之一。如果yt =1的機率為yp ，則yt =0的機率為 1- yp。機率可以表示如下：

將所有輸入資料的 P 相乘即可得到概似函數 Lk。

概似函數就是總機率，從上面機率的描述來看，越大越好！
稍微解釋一下概似函數的組成。

參考 https://en.wikipedia.org/wiki/Likelihood_function 的範例段落，我們可以得出結論：

對於同一個似然函數，在它所代表的模型中，某個參數值有多種可能性，但如果存在一個參數值使得似然函數的值最大化，那麼這個值就是最「合理」的參數值。

例如，假設有 10 個數據，確定其中 4 個為類別 1（機率為yp），另外 6 個為類別 0（機率為 1- yp），因此範例中描述的概似函數為:

假設m個數據，則確定n個數據被分類為1（機率為yp），其餘m-n個數據被分類為0（機率為1- yp），因此範例中描述的概似函數為: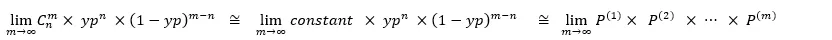

傳回概似函數Lk，兩邊取對數：

接下來定義損失函數：概似函數越大越好，但損失函數越小越好，所以概似函數乘以負值；損失函數值會隨著資料項數量成比例增加，所以取平均值使其不受檔案數量影響。

機率越大，準確率越高，機率越大，準確率越高，在得到的機率最大的情況下，對應得到的W向量為：
(1) 最大化所有資料乘P的似然函數

(2) 最大化識別結果的機率

(3) 誤差最小化（損失函數結果最小）

所以損失函數是：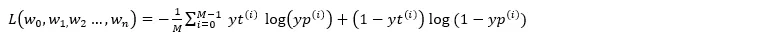

結合梯度下降法對每個w求導，可得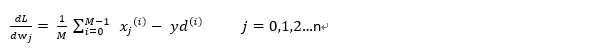

邏輯迴歸（k代表迭代次數）：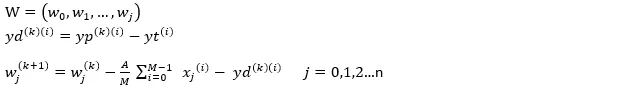

A 可當作是學習率超參數。

參考資料：

https://rasbt.github.io/mlxtend/user_guide/classifier/LogisticRegression
https://msu-cmse-courses.github.io/cmse202-S23-jb/daily/Day-15/Day-15_In-Class_ML-LogisticRegression-STUDENT.html
https://rasbt.github.io/mlxtend/user_guide/classifier/SoftmaxRegression
https://en.wikipedia.org/wiki/Logistic_regression