嗨～ 今天要來分享我是如何解2D的動態規劃問題。所謂的2D就是要考慮的因素（會影響到每個子問題結果）變多了。以前分享過的1D動態規劃，基本上只需要考慮子問題間的關係（例如dp[n] = dp[n - 1] + dp[n -2]），現在讓我們看看2D的動態規劃問題吧

Leetcode 62. Unique Paths

題目敘述：有一個機器人位於一個 m x n 的的網格的最左上角，這個機器人如果要到達網格的右下角。他可以有幾種走法。他只能往下走或往右走。

Example:

(圖源：leetcode)

分析：
我們可以先讓機器人離終點近一點，當他走到終點時回傳1，代表這是一種走法。那麼我們的問題變成要如何從原先的起點（左上角）走到那個離終點很近的地方。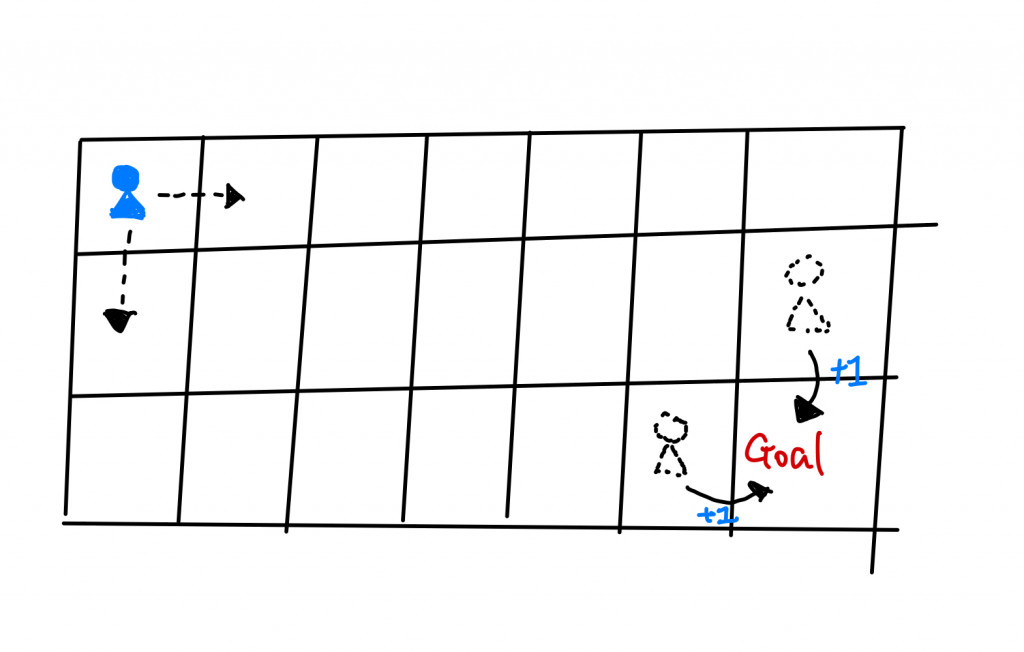

機器人的選擇始終只有向下走或向右走，這代表我們可以利用決策樹來視覺化他的每一個選擇，而說到樹狀結構，利用DFS走向終點是一個很直覺的想法。

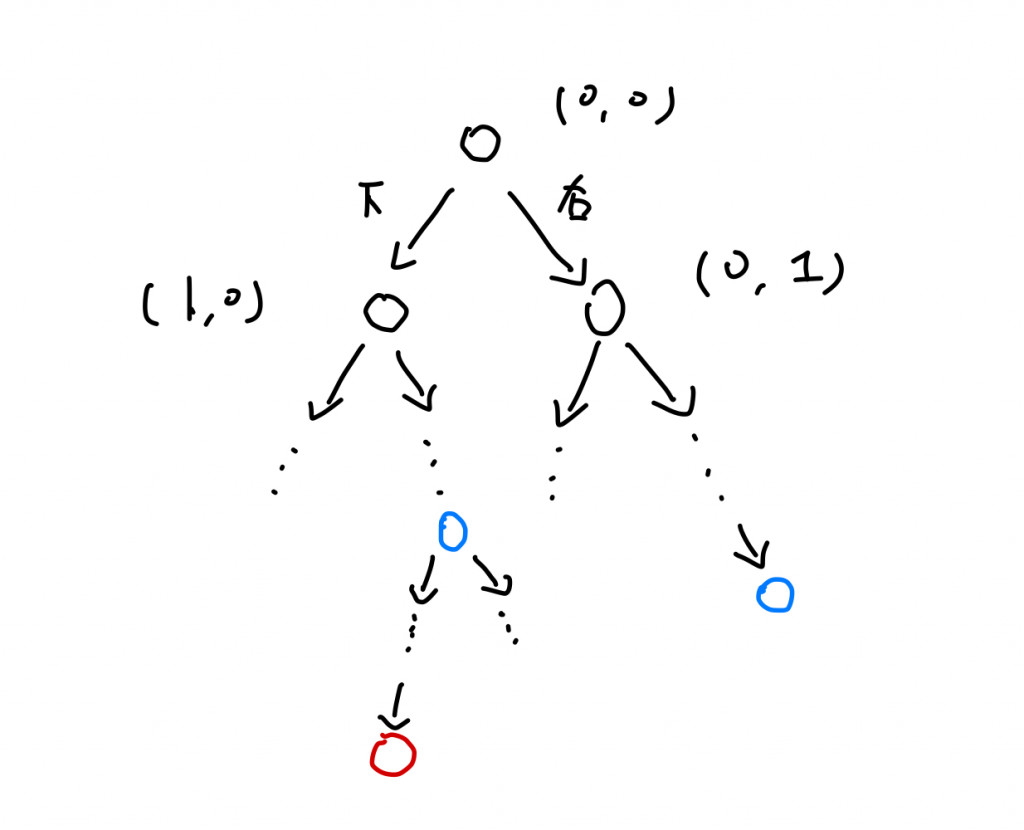
上圖可以看出，每個選擇會讓機器人走到在網格中的某個位置（利用二維陣列的index i, index j表示）
這時候就是動態規劃可以介入的時候了！我們可以利用Memoization的動態規劃解題手法去儲存每個已經看過的座標通往終點的走法。當機器又走到相同的座標（如藍色的節點）我們可以馬上回傳結果。

以Python程式碼實作

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        cache = {}

        def dfs(row, col):
            if row == m or col == n:
                return 0

            if row == m - 1 and col == n - 1:
                return 1

            if (row, col) in cache:
                return cache[(row, col)]
            
            cache[(row, col)] =  dfs(row + 1, col) + dfs(row, col + 1)
            return cache[(row, col)]
        
        return dfs(0, 0)

時間複雜度：O(m*n)，因為access了網格中的每一個cell

我們之前在1D動態規劃也提到可以利用Bottom up的方法去解題（當然要想出這種方法的難度比較高），所以我們來看看要如何以這種方式解題。

分析二：
我們假設dp[(i, j)]代表從起點走到座標(i, j)共有幾種方法，並且經由觀察可以發現dp[(i, j)] = dp[(i, j - 1)] + dp[(i - 1, j)]，為了優化空間複雜度我們每一次都只使用「兩列」。因為某一格只會受到上一次的同一格以及跟他同一列的前一格影響。如圖所示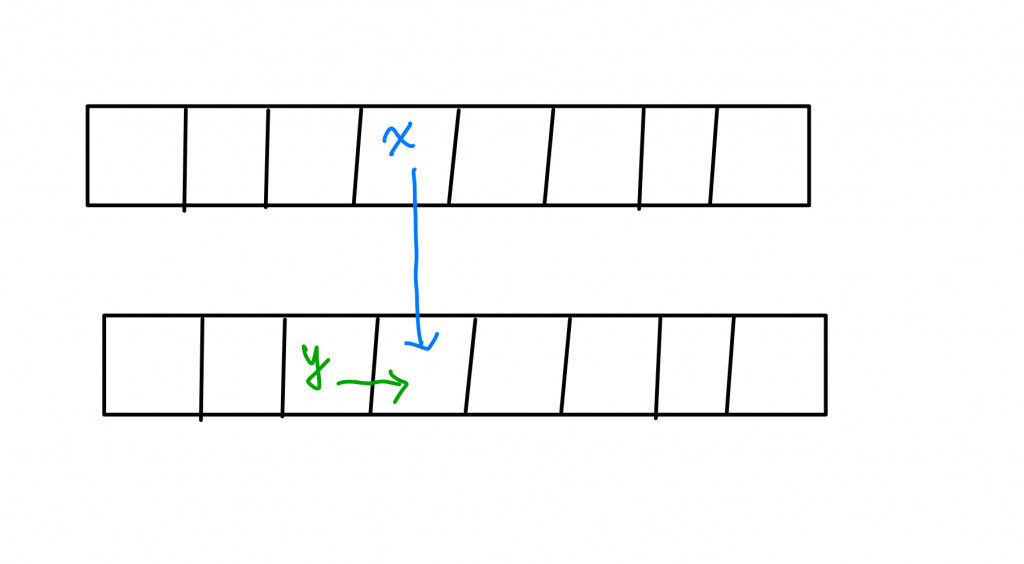

所以我們只需要兩個一維的list: prev, cur。
在以程式實作時，我們會先初始化prev的陣列，並讓prev[0] = 1，其餘為0，好讓程式可以正確的運算下去。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        prev = [0 for _ in range(n)]
        prev[0] = 1

        for _ in range(m):
            cur = [0 for _ in range(n)]
            for i in range(n):
                if i - 1 >= 0:
                    cur[i] += cur[i - 1]
                cur[i] += prev[i]
            
            prev = cur
        
        return prev[-1]

Follow up: Leetcode 63. Unique Paths II

敘述：如果這個grid中有一個障礙物，機器人只能繞過它，那有幾種走法可以到達中點（一樣只能選擇向左或向右）
解法：幾乎跟上題一樣，只需要檢查現在是否走到障礙物的座標，若是則讓該dp[(i, j)]指定為0。

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        M, N = len(obstacleGrid), len(obstacleGrid[0])
        prev = [0] * N
        prev[0] = 1
        
        for i in range(M):
            cur = [0] * N
            for j in range(N):
                if obstacleGrid[i][j] == 1:
                    cur[j] = 0
                else:
                    if j - 1 >= 0:
                        cur[j] += cur[j - 1]
                    cur[j] += prev[j]
            
            prev = cur
        
        return prev[-1]

Follow up: Leetcode 980. Unique Paths III

敘述：現在機器人的起點和要到達的終點不一定是左上以及右下角了。另外障礙物可以不只有一個。除此之外，在到達終點之前機器人需要經過所有不是障礙物的座標，請問這樣會有幾種走法？

分析：

• 我們要先找出起點以及總共有多少個座標是可以經過的。
• 現在機器人的選擇有四個方向，要注意不要走出邊界。
• 在走訪那些並非障礙物以及並非終點的座標時我們要紀錄已經走過哪些座標了（避免走回頭路）
• 另外當我們紀錄的走訪過的座標數量達到可以走訪的座標的上限時，代表已經準備好要走到終點了。

class Solution:
    def uniquePathsIII(self, grid: List[List[int]]) -> int:
        M, N = len(grid), len(grid[0])
        upperbound = 0
        start = None
        
        for i in range(M):
            for j in range(N):
                if grid[i][j] == 1:
                    start = [i, j]
                    upperbound += 1
                elif grid[i][j] == 0:
                    upperbound += 1
        
        def dfs(row, col, visit):            
            if grid[row][col] == -1:
                return 0
            
            if grid[row][col] == 2:
                return 1

            nums = 0
            visit.add((row, col))

            for x, y in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                if (row + x, col + y) in visit:
                    continue
                if (row + x < 0 or
                    row + x == M or
                    col + y < 0 or
                    col + y == N):
                    continue
                elif grid[row + x][col + y] == 2 and len(visit) < upperbound:
                    continue
                else:
                    nums += dfs(row + x, col + y, visit.copy())
            
            return nums
        
        return dfs(start[0], start[1], set())
            

Leetcode 309. Best Time to Buy and Sell Stock with Cooldown

題目敘述：給予一個input array叫prices，prices[i]代表第i天的股價。題目的目標是找出最大的利益。你可以選擇多次的買進和賣出但有以下限制：1. 每天可以選擇交易或是不交易 2.買入後一定要先賣出才能再次買入 3. 賣出後要等待一天才能再次開始決定是否要買入（After you sell your stock, you cannot buy stock on the next day ）

Example:

Input: prices = [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]

分析：我們有兩種選擇，忽略當天的交易、啟動交易，而且交易時會遵守「買進、賣出、忽略、買進、賣出...」的條件。所以我們需要一個變數紀錄忽略的情況；另一個用來表示交易的情況，因為要具備買進和賣出這種反轉的性質，我們的資料型態設定為Boolean，True的時候代表可以買進，False實則代表可以賣出。

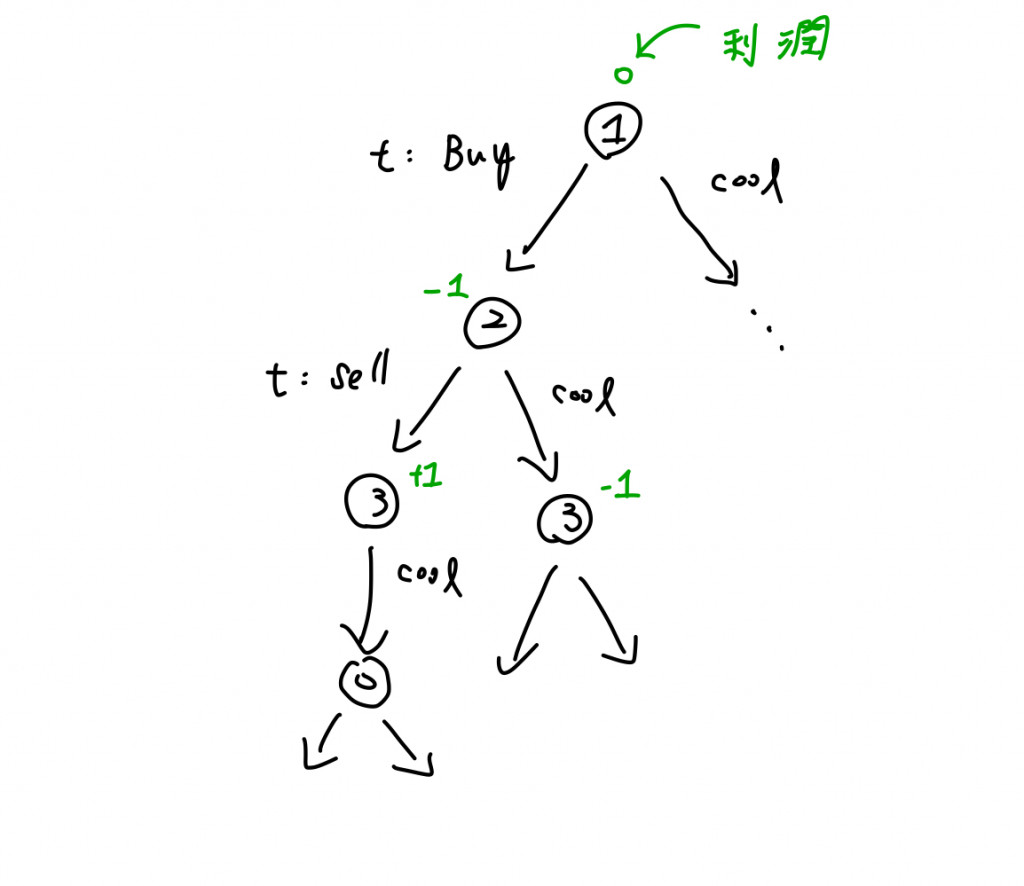
透過決策樹，我們就可以利用Memoization來解題。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        dp = {}

        def dfs(i, buying):
            if i >= len(prices):
                return 0
            if (i, buying) in dp:
                return dp[(i, buying)]
            
            cooldown = dfs(i + 1, buying)
            if buying:
                dp[(i, buying)] = dfs(i + 1, not buying) - prices[i]
            else:
                dp[(i, buying)] = dfs(i + 2, not buying) + prices[i]

            dp[(i, buying)] = max(dp[(i, buying)], cooldown)
            return dp[(i, buying)]
        
        return dfs(0, True)

明天我們再繼續欣賞經典的2D動態規劃問題