Hi，昨天分享了一些光看題目就知道很適合利用2D動態規劃去解決的問題。今天要繼續來分享屬於2D動態規劃的經典問題，和相關應用。

0/1背包問題

敘述：

• 有一個容量為X的背包
• 有一個展示櫃，裡面放著各種重量不同、價值也不同的寶石
• 目標：在容量的限制內，選擇的寶石要有最大的總價值
• 每種寶石只有一個，選擇或不選擇（所以才叫0/1）

我們再把問題整理得更像程式語言一些。

capacity = 10
weight = [1,6,3,2,4]
profit = [3,5,4,1,7]
# Goal: 在限制為10單位的情況下，選擇出的那些item他們的profit總和是能選的最大值

分析：我們可以「選擇」或「不選擇」當下的item，並且想「選擇」某個item的前提是當下的capacity不小於weight[i]。在選擇此item後，我們的total profit增加、capacity減少，繼續針對下一個item決定要「選擇」或是「不選擇」。看到這裡應該就很清楚上述的敘述可以轉化成決策樹。

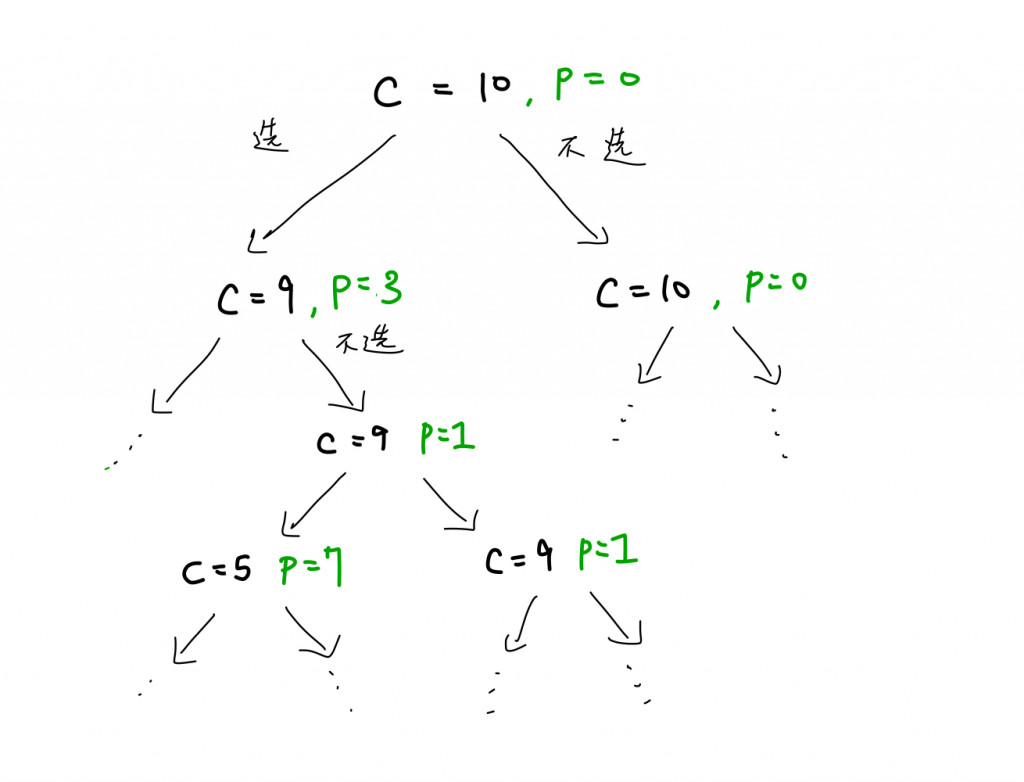
當有了決策樹、之後只要加入一個hash map來儲存那些已經以(index, capacity)這兩個因素所控制的節點就能以memoization解決0/1背包問題。

cache = {}

def memoization(cap, index):
    if index == len(weight):
        return 0
    if (index, cap) in cache:
        return cache[(index, cap)]
    
    cache[(index, cap)] = memoziation(cap, index + 1)

    if cap + weight[index] <= capacity:
        p2 = value[index] + memoziation(cap + weight[index], index + 1)
        cache[(index, cap)] = max(cache[(index, cap)], p2)
    
    return cache[(index, cap)]

ans = memoization(0, 0)
print(ans)

如果覺得上述的解法不滿意，一定要使用所謂的True Dynamic Programming(a.k.a Bottom up)的話，那就繼續看下去吧～

分析：影響我們選擇的因素：當前的容量、物品的重量，我們可以把這些畫成二維的陣列。從上到下、從左到右每個空格代表在某個重量下，若有這麼多個item可以選並且我選了當下這個item可以得到的最大價值為多少。

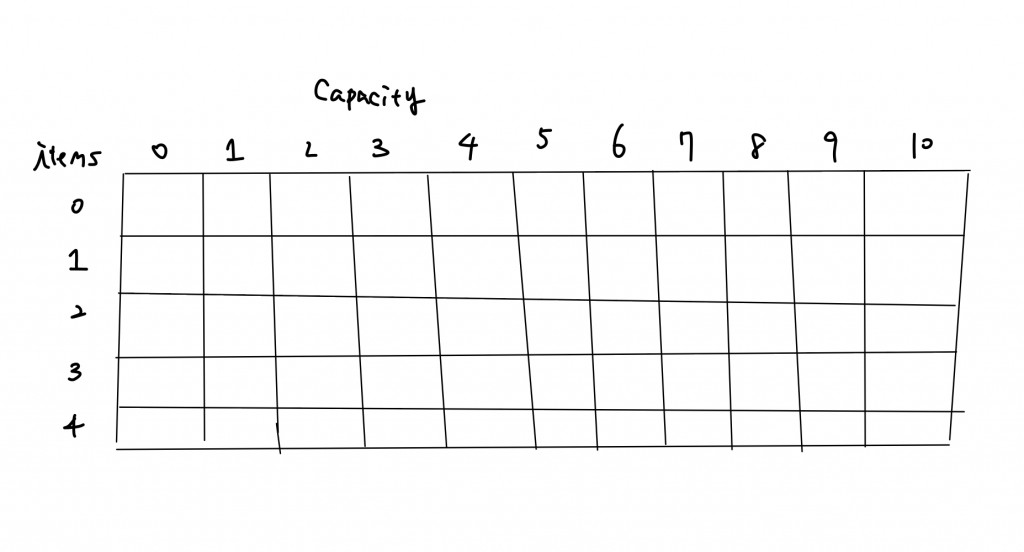
現在我們只有一個item時，當我們的容量從0到10時：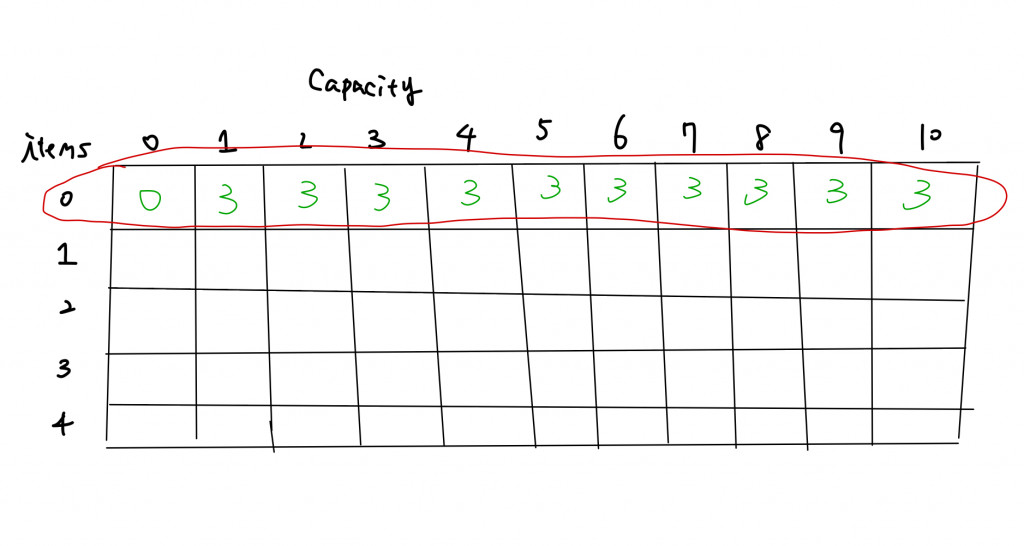

當我們有兩個item時，我們想要選擇item1，當我們的容量不足時，我們只能放棄，這時會向上查看是否能選擇item0（黑色數字3）。當我們有足夠的容量就選擇item1，當我們選擇完item1後根據剩餘的容量去選擇相應的價值，即：選擇dp[i - 1][capacity - 6]，也就是藍色圓圈圈起來的數字。

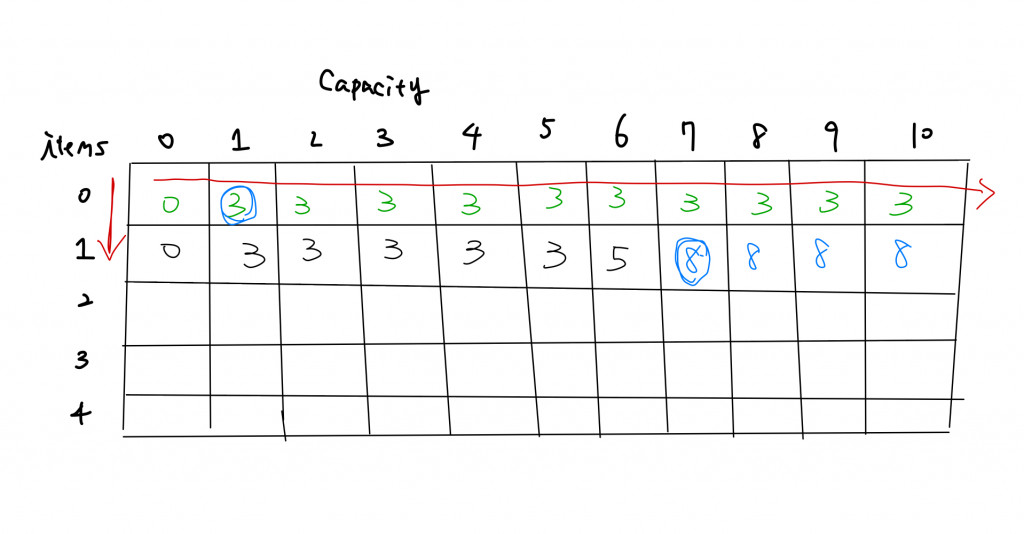
我們在計算時其實不需要整個二維陣列，每次只需要兩列，因為現在正在計算的列，只會使用到上一列的。

def trueDP(weights:list[int], values:list[int], capacity:int)->int:
    prev = [0] * (capacity + 1)
    curr = [0] * (capacity + 1)

    for item in range(len(weights)):
        for cap in range(1, capacity + 1):
            if cap >= weights[item]:
                curr[cap] = max(prev[cap], values[item] + prev[cap - weights[item]])
            else:
                curr[cap] = prev[cap]
        prev = curr
        curr = [0] * (capacity + 1)
    
    return prev[-1]

if __name__ == "__main__":
    capacity = 10
    weight = [1,6,3,2,4]
    profit = [3,5,4,1,7]
    print('the max profit : ',  trueDP(weight, profit, capacity))

Leetcode 416. Partition Equal Subset Sum

題目敘述：給予一個整數的array，判斷這個array是否可以分成兩堆，並且兩堆的值一樣？

Example:

Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].

分析：

• 想要將array分成兩堆一樣的值，首先要確定array的總和為偶數
• 如果總和為偶數，將總和除以2後，就是我們的"capacity"
• 根據題目的要求，我們要選擇的數字要到達這個capacity
• 我們對於array中的某個數字有「選取」或是「不選」
• 我們可以利用set去紀錄我們決策的結果（把選擇和不選的結果都加入到set中）

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        capacity = sum(nums)
        if capacity % 2 != 0:
            return False
        
        capacity //= 2
        dp = set()
        dp.add(0)

        for i in range(len(nums)):
            nextDp = set()
            for n in dp:
                if nums[i] + n == capacity:
                    return True
                nextDp.add(nums[i] + n) # choose this number
                nextDp.add(n)        # not choosing this number
            
            dp = nextDp

        return False

解題的模板基本上和0/1背包問題一樣，只是因為我們只需要去在意選擇的item的重量，所以可以更加去優化解題的手段。