合併排序法 (Merge Sort)

合併演算法input array不斷分成兩半，直到不能再分(剩一個element)，再兩兩合併各組資料，合併時排序，再合併直到排好整個資料為止。平均時間複雜度為O(nlogn)，但跟bucket sort一樣空間複雜度較高O(n)。見以下圖說明。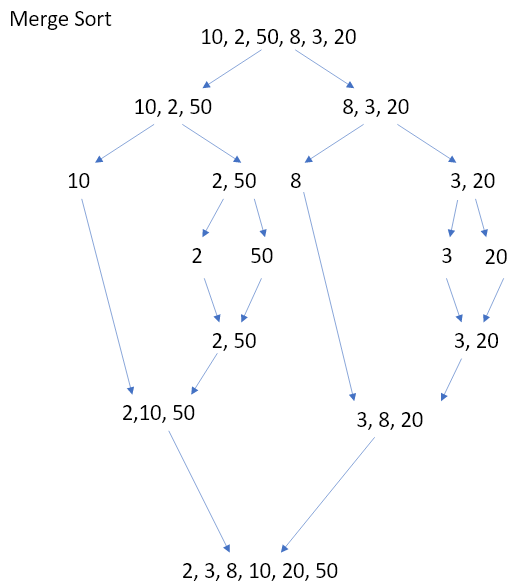

圖1 合併排序法示意圖。

def mergeSort(mylist):
    if len(mylist) < 2:
        return mylist
    else:
        mid = len(mylist)//2
        leftlist = mylist[:mid]
        rightlist = mylist[mid:]
        return merge(mergeSort(leftlist), mergeSort(rightlist))


def merge(left, right):
    result = []
    while len(left) and len(right):
        if left[0] < right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    if len(left):
        result += left
    else:
        result += right
    return result

mylist = [10, 9, 20, 2, 16, 8]
print(mergeSort(mylist))
>> [2, 8, 9, 10, 16, 20]

快速排序法 (Quick Sort):

首先，命第一個值作為基準值(pivot)，同時將swap指標指向它，然後往下看，當遇到值小於基準值pivot時，swap指標+1，將那個值與swap指標指向的值交換，然後繼續看array的下個值，直至把整個array看完。然後將pivot跟swap指標指向的直互換。這時我們可以觀察到pivot左邊的值皆小於pivot，其右邊的值皆大於pivot。於是我們用同樣的方式處理pivot左邊於右邊的array，直至不能再分。其實時間複雜度為O(nlogn)，空間複雜度為O(n)。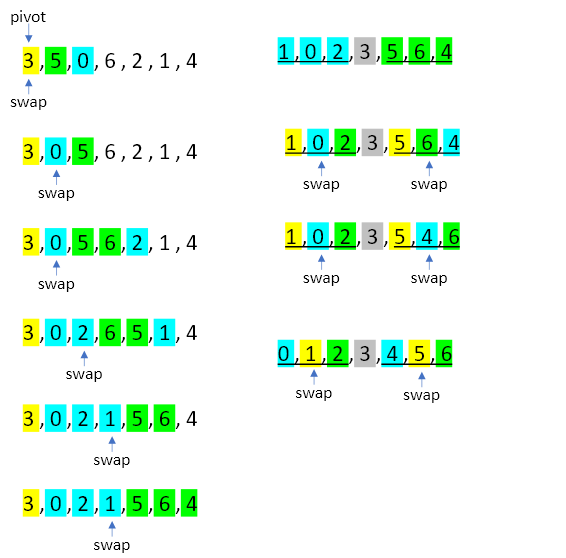

圖2 快速排序法式意圖。

def swap(mylist, index1, index2):
    mylist[index1], mylist[index2] = mylist[index2], mylist[index1]

def pivot(mylist, pivot_index, end_index):
    swap_index = pivot_index
    for i in range(pivot_index+1, end_index+1):
        if mylist[i] < mylist[pivot_index]:
            swap_index += 1
            swap(mylist, swap_index, i)
    swap(mylist, pivot_index, swap_index)
    return swap_index

def QuickSort(mylist, left, right):
    if left < right:
        pivot_index = pivot(mylist, left, right)
        QuickSort(mylist, left, pivot_index-1)
        QuickSort(mylist, pivot_index+1, right)
    return mylist

def Quick(mylist):
    left = 0
    right = len(mylist)-1
    return QuickSort(mylist, left, right)

my_list = [3, 5, 0, 6, 2, 1, 4]
print(Quick(my_list))
>> [0, 1, 2, 3, 4, 5, 6]

堆積排序法(Heap Sort)

大家還記的我們之前講的min-heap還有max-heap嗎?Heap Sort借用了一些Binary Heap的概念。但如果真的照之前做的insertnode會發現，只有root和children間有排序，同一個parent不同children間並沒有排到，所以改成下面的作法，我覺得蠻神奇的蠻難自己想到的~
時間複雜度:O(nlogn), 空間複雜度:O(1)

def heapify(customList, n, i):
    # the index of the smallest number
    smallest = i
    # left child and right child
    l = 2*i+1
    r = 2*i+2
    if l < n and customList[l] < customList[smallest]:
        smallest = l
    if r < n and customList[r] < customList[smallest]:
        smallest = r
    if smallest != i:
        customList[i], customList[smallest] = customList[smallest], customList[i]
        heapify(customList, n, smallest)

def heapSort(customList):
    n = len(customList)
    # 將每一個有children的node和他們的children做筆記和排序
    for i in range(n//2-1, -1, -1):
        heapify(customList, n, i)
    #這步我覺得挺神奇的，如果實際畫畫看，真的就把剩下沒排完的全部排好
    for i in range(n-1, 0, -1):
        customList[i], customList[0] = customList[0], customList[i]
        heapify(customList, i, 0)
    customList.reverse()


cList = [2, 1, 9, 8]
heapSort(cList)
print(cList)
>> [1, 2, 8, 9]

但其實python就有module在做這件事，大家可以看看heapq的文件，看看怎麼操作，以下為文件內的範例:

import heapq
def heapsort(cList):
    h = []
    for value in cList:
        heapq.heappush(h, value)
    return [heapq.heappop(h) for i in range(len(h))]
    
cList = [2, 1, 9, 8]
print(heapsort(cList))
>> [1,2,8,9]

那下面總結一下，不同sorting方法的時間、空間複雜度: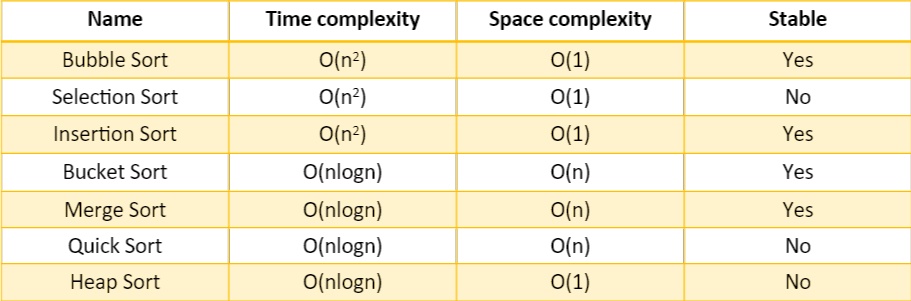

好囉~那明天我們繼續來看搜尋演算法~

參考資料:
本文主要為udemy課程: The Complete Data Structures and Algorithms Course in Python的學習筆記，有興趣的人可以自己上去看看。