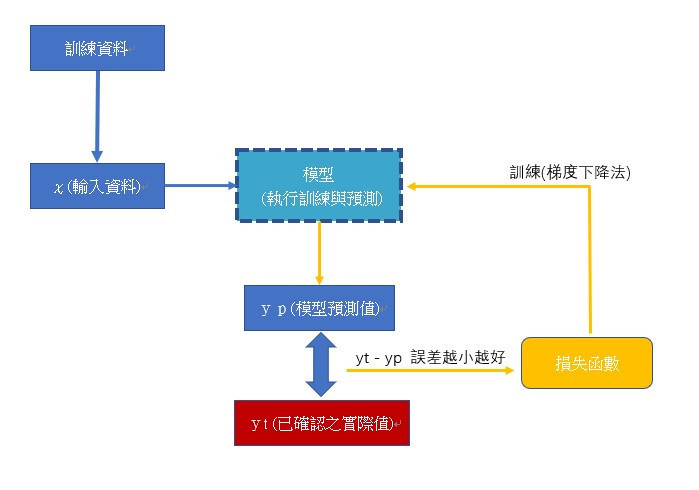
上一篇文章提到了 logistic single classification，解釋如何實現的一些細節。接下來要探索的是邏輯斯多類別分類。

如果Logistic單分類是單分類器，則Logistic多類別分類是：

(1) 多類分類器。
(2) 權重是一個矩陣，其維度為{特徵數} × {類別數}。
(3) 輸入資料的矩陣為其維度：{資料數量} × {特徵數量}。

差別在於，單（binary）分類權重是單一向量，而多類權重由於分類數量較多，是一個矩陣。

Single Classifier for Logistic Regression: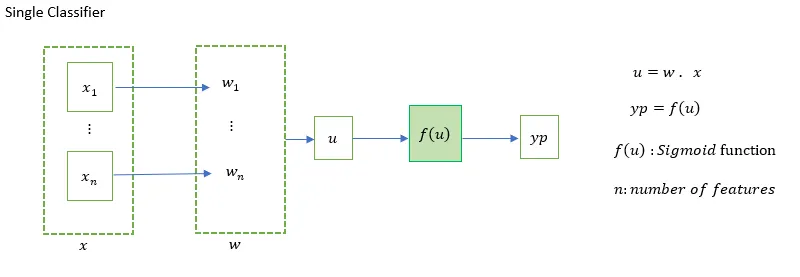

Multi-class Classifier for Logistic Regression: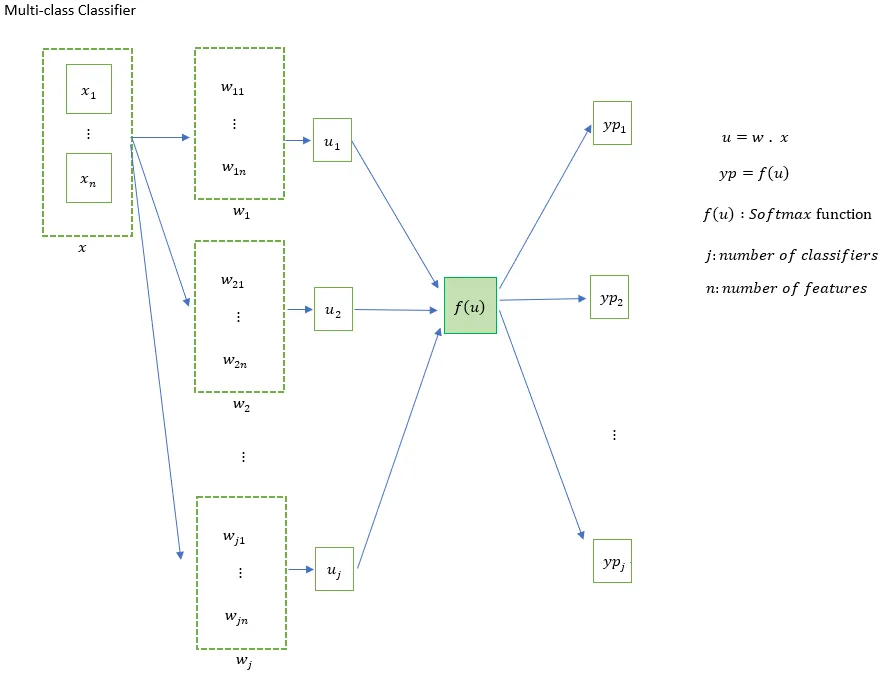

注意這裡的Softmax是：

透過加入多層分類器來增加學習的深度，經過層層過濾後，某些情況會增加估計值的準確性，只有實際測試才知道。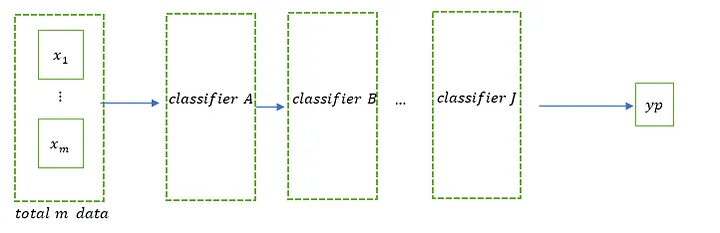

這裡要注意的是矩陣運算。

讓我們來比較一下單分類器和多類別分類器：

Single Classifier

假設資料{X}有100個條目，3個特徵字段，權重向量W中有3個元素，程式必須注意維度是否正確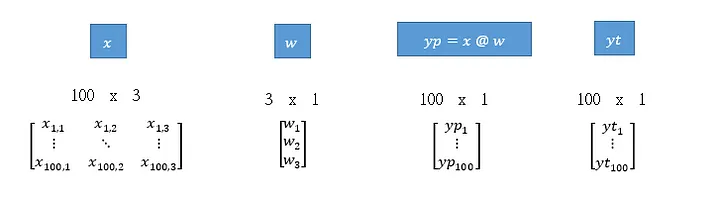

Multi-class Classifier

假設資料{X}有100個條目、3個特徵欄位、3個類別，權重向量W有3x3個元素，程式必須注意維度是否正確

概念重點

1. 一切的源頭就是找到損失函數，利用梯度下降法對損失函數各個特徵的權重變數進行微分，以便訓練並找出各個特徵
   最適合的權重值。回頭做很多過去的數據或未來的數據：
   （1）回歸
   （2）分類

2. 邏輯迴歸的損失函數來自誤差的平方。直接的意義就是最小化特徵權重所產生的預測值的誤差。

3. Logistic單分類（binary classifier）可以看作是單分類器，透過Sigmoid啟動函數，將預測值壓縮到
   0到1之間，轉換為機率的概念。損失函數源自概似函數。
   透過機率 來自交叉熵，然後在損失函數上微分梯度下降的概念，得到特徵權重，以最大化分類預測的機率。
   另一個意義是出錯的機會變小了。

4. Logistic多重分類是將多個單分類器權重向量組合成一個權重矩陣，利用Softmax活化函數透過機率來判斷分類，每
   個資料預測的每個分類的機率總和為1。讓預測結果屬於哪個類別，哪個類別的機率值最高，而機率對應實際值，而
   代表反演的權重矩陣也有助於最小化未來預測結果的誤差。

5. 隱藏層可以用特徵權重矩陣進行計算，然後利用Sigmoid、Softmax、ReLU等標準化資料值的壓縮，使其變成類似機
   率的值；隱藏層可以是多層的，最後一層可以產生最終的預測分類，其意義也意味著透過將隱藏層轉換為機率的方
   式，經過層層過濾和判斷，得到最好的分類將利用總機率的概念來獲得預測。

參考資料：

https://www.kaggle.com/code/manishkc06/multi-class-logistic-regression-beginner-s-guide
https://en.wikipedia.org/wiki/Multinomial_logistic_regression
https://en.wikipedia.org/wiki/Softmax_function
https://hackmd.io/@Kuihao/Softmax_Derive
https://zhuanlan.zhihu.com/p/105722023