本文同步更新於個人網站中，有更好的排版和程式碼區塊 highlighting 支援。

前面幾天我們已經學習了各種線性資料結構，都說資料結構是用來儲存資料，那我們總不可能存進去後就再也不管它了吧？肯定是為了將來再把拿出來使用，那麼問題來了，我們要如何去從一堆資料中找出我們要的那筆資料呢？

這時候就要考驗我們如何去設計一個好的搜尋演算法，讓我們可以在最短的時間內找到我們要的資料。今天我們就來學習兩個常見的搜尋演算法，分別是循序搜尋（Sequential Search）和二分搜尋（Binary Search）。

循序搜尋 Sequential Search

循序或是線性搜尋（Linear Search）是最基本的搜尋演算法，它的概念是將每一個資料結構中的元素和我們要找的元素做比較，直到找到相同的元素為止。

我們在尋找過程有可能在第一個元素就找到，也有可能在最後一個元素才找到，或者是根本找不到。在最壞的情況下，我們需要將所有元素都比較一次，因此時間複雜度為 O(n)，是一種比較低效的搜尋演算法。

下面是循序搜尋的程式碼實作：

const DOES_NOT_EXIST = -1;

function sequentialSearch(arr, value) {
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === value) return i;
  }
  return DOES_NOT_EXIST;
}

實作很簡單，就是直接迭代整個陣列，並將每個陣列元素和搜尋目標做比較，如果找到相同的元素，演算法就會回傳一個值來表示搜尋成功。回傳值可以是元素的索引，或者是一個布林值；如果沒有找到就回傳一個 -1 或 false 等等。

二分搜尋 Binary Search

循序搜尋適合用在未排序的資料中，但是如果資料已經排序過了，我們就可以使用更快速的搜尋演算法來加速整個搜尋過程，讓複雜度降低到 O(log n)。而我今天要介紹的就是二分搜尋法（Binary Search）。

Binary Search 是一種在已排序的資料中尋找目標值的搜尋演算法。它的原理和猜數字遊戲很像，例如在 1 ~ 100 範圍內猜一個數字，然後出題者會根據你猜的數字給你一個提示，例如「太大了」、「太小了」或是「猜對了」，然後我們根據提示來縮小範圍，直到猜對為止。

Binary Search 的步驟

1. 先找到陣列的中間值。
2. 將中間值和目標值做比較，如果中間值等於目標值，那麼搜尋結束。
3. 如果目標值比中間值小，則回到步驟 1 並在中間值的左邊子陣列中尋找。
4. 如果目標值比中間值大，則回到步驟 1 並在中間值的右邊子陣列中尋找。

實作

在開始之前我們要先確認一件事，就是我們的陣列必須是已經排序過的，如果沒有排序過，我們就必須先對陣列做排序，確認已經排序過之後，我們就可以開始利用 binary search 來尋找目標值了。

function binarySearch(arr, target) {
  let left = 0;
  let right = arr.length - 1;

  while (left <= right) {
    const mid = Math.floor((left + right) / 2);

    if (arr[mid] === target) {
      return mid;
    }

    if (arr[mid] < target) {
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }

  return -1;
}

整個搜尋過程如下圖所示：

練習

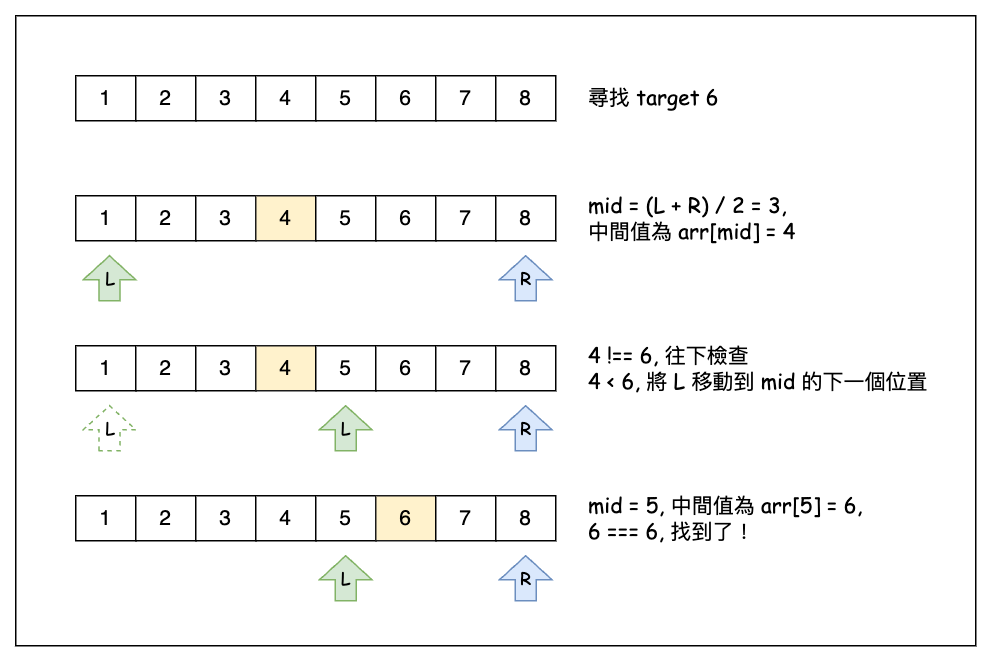
我們來看幾道關於 binary search 的題目：

首先是 704. Binary Search，這題其實就是要你實作 binary search，我們直接拿剛才的程式碼套進去就可以了，可以試著自己再實作一次看看。

Search Insert Position

接下來我們來看 35. Search Insert Position，題目如下：

給你一個已經排序過的陣列 nums 和一個目標值 target，如果目標值存在於陣列中，則回傳目標值的索引，如果目標值不存在於陣列中，則回傳目標值應該被插入的位置索引。另外要求你必須在 O(log n) 的時間複雜度內完成。

例如：

target 存在於陣列中：

Input: nums = [1,3,5,6], target = 5
Output: 2

target 不存在於陣列中：

Input: nums = [1,3,5,6], target = 2
Output: 1

思路：其實也是一個基本的 binary search，只是當 target 不存在於陣列中時，我們要回傳的是 left 的值，因為 left 的值就是 target 應該被插入的位置索引。實作如下：

function searchInsert(nums, target) {
  let left = 0;
  let right = nums.length - 1;

  while (left <= right) {
    const mid = left + Math.floor((right - left) / 2);

    if (target === nums[mid]) {
      return mid;
    }

    if (target < nums[mid]) {
      right = mid - 1;
    } else {
      left = mid + 1;
    }
  }

  return left;
}

Find Peak Element

最後我們來看 162. Find Peak Element，題目如下：

給你一個陣列 nums，你需要找出一個 peak element，peak element 的定義是：陣列中的一個元素，大於左右相鄰的元素。你可以假設 nums[-1] = nums[n] = -∞，也就是說陣列的邊界元素是負無限大，此外陣列中可能存在複數個 peak element。現在要請你寫一個時間複雜度為 O(log n) 的演算法來解決這個問題。

例如：

Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 是一個 peak element，因為 3 大於左右相鄰的元素 2 和 1。

Input: nums = [1,2,1,3,5,6,4]
Output: 1 or 5
Explanation: 這個陣列有兩個 peak element，1 和 5，你可以回傳任何一個。

思路：直覺反應一定是直接迴圈把每一個都掃過一次檢查看是不是 peak，但是這樣的複雜度是 O(n)，題目要求我們必須在 O(log n) 的時間複雜度內完成，所以我們要使用 binary search 來解決這個問題。這題和前面的 binary search 稍微不同的地方在於，我們要找的不是一個特定的值，而是一個條件，也就是 peak element，我們可以從中點元素和它的右邊鄰居的大小關係來縮小搜尋範圍：

• 如果 nums[mid] < nums[mid + 1]，那麼在 mid 的右邊一定存在一個 peak element。
• 如果 nums[mid] > nums[mid + 1]，那麼在 mid 的左邊一定存在一個 peak element。

實作程式碼如下：

function findPeakElement(nums) {
  let left = 0;
  let right = nums.length - 1;

  while (left < right) {
    const mid = Math.floor((right + left) / 2);

    if (nums[mid] > nums[mid + 1]) {
      right = mid;
    } else {
      left = mid + 1;
    }
  }

  return left;
}

總結

我們比較兩種搜尋法後應該會注意到一件事，如果我們今天在存資料的時候，有事先整理過的話，那麼就可以減少我們將來搜尋的時間，像是我們對資料做了排序後，就可以使用 binary search 來加速搜尋的過程，而不用使用循序搜尋。甚至我們可以使用 hash table 來儲存資料，這樣我們就可以在 O(1) 的時間複雜度內找到我們要的資料。

這也是為什麼我們在設計資料結構的時候，要考慮到我們將來會怎麼使用這些資料，如果我們知道我們將來會需要對資料做搜尋，那麼我們就要考慮到如何將資料排序分類，或是使用一些特定的資料結構來儲存資料。

參考資料

• 《Learning JavaScript Data Structures and Algorithms, 3/e》