本文同步更新於個人網站中,有更好的排版和程式碼區塊 highlighting 支援。
動態規劃(Dynamic Programming, DP)一般在面試時多作為壓軸題出現,它在現實中的用途極廣,並且通常有著不錯的效能表現。動態規劃的題目一般有以下特點:
此外,原問題還會給出當某個值為 0 或者 1 時的解,我們可以用利用這些初始“狀態”推導填表格時用的公式,這個公式被稱為狀態轉移方程。
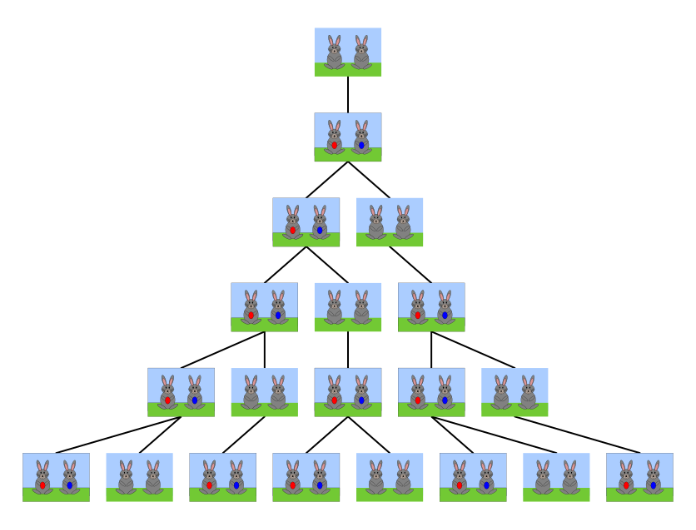
費氏數列(費波那契數列),義大利人 Leonardo Fibonacci 他在描述兔子生長的數目時用上了這數列。假設一對剛誕生的兔子要等一個月才會到成熟期,而一對成熟的兔子每個月可以生一對小兔子,那麼從一對新生兔子開始,且兔子永不死去,求解 n 個月後兔子的總數。如下圖所示:
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... |
|---|---|---|---|---|---|---|---|---|---|---|
| 兔子總數(對) | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | ... |
| 可生育兔子數(對) | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | ... |
經過觀察可以發現,除了最初兩項等於 1 以外,每一項都等於前兩項之和。
接著我們用費式數列當作例子來幫助我們理解上面提到比較晦澀的概念以及體驗一下動態規劃的高效。許多題目都可以用多種不同思路去解決,我們會從最簡單的暴力法開始,慢慢過渡到動態規劃的解法。
直接透過遞迴的方式求解,實作如下:
function fib(n) {
if (n === 1 || n === 2) return 1;
return fib(n - 1) + fib(n - 2);
}
console.log(fib(12)); // 144
這種方法的效能非常差,我們將遞迴呼叫用樹狀圖表示出來,如下圖所示:
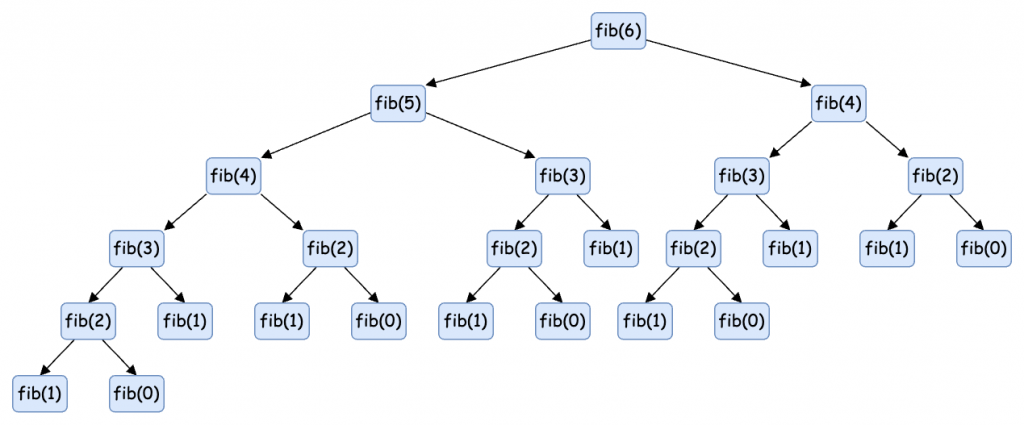
此時我們會發現裡面存在很多函式被多次呼叫,例如:fib(3) 被呼叫了 3 次,也就是說同一個子問題 fib(i) 會被處理很多次。這些遞迴函式的執行次數為二元樹的節點數。顯然二元樹的總節點數為指數級別,所以子問題的個數為 ,當你的 n = 50 時,瀏覽器可能就會卡住不能動了。
此時就需要使用動態規劃來解決這個問題了,我們可以用兩種方法來改進剛才的暴力法:
其實就是多了一個 cache,然後從上而下遞迴從大問題開始解決,遇到重複子問題時,就從快取中取出答案,避免重複計算。這種方法稱為記憶化(Memoization)。
通常我們會用一個 hash 當作快取(cache),我們可以把 cache 放入 fib 函式中。當參數傳入時,先檢查 cache 中是否有答案,沒有才進行計算,這樣整個數列的 fib(6)、fib(5)、fib(4)、fib(3)、fib(2)、fib(1) 都只會計算一次,效能也提升到了 O(n) 的時間複雜度。如下圖:
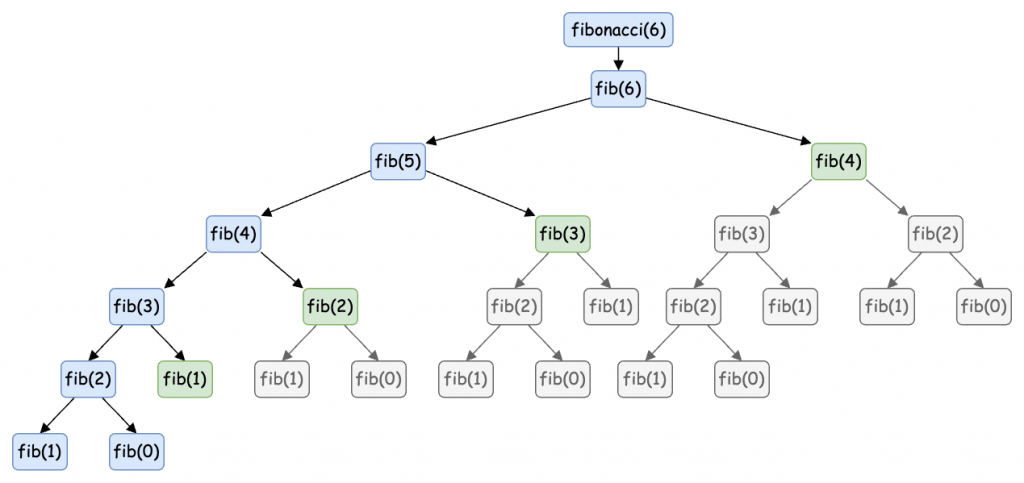
我們可以從圖中觀察 Memoization 的過程是從 fib(6) 一路呼叫到 fib(1) 與 fib(2) 時,fib(3) 就會有答案,然後向上折回。在遞迴呼叫的 tree 中,綠色的節點被重複執行但是因為已經計算過了,所以會直接從 cache 中取出答案,不會再重複計算。實作程式碼如下:
function fibonacci(n) {
const cache = { 0: 0, 1: 1, 2: 1 };
function fib(n) {
if (cache[n] !== undefined) return cache[n];
cache[n] = fib(n - 1) + fib(n - 2);
return cache[n];
}
return fib(n);
}
console.log(fibonacci(100)); // 354224848179262000000
透過記憶化的方式,我們知道了快取的重要性,其實這些參數是從 1 到 n 遞增的,因此我們可以直接用一個陣列來保存結果。然後在迴圈中將前面兩項的值相加就是目前項的解,然後又把這個解放入陣列中,又可以求出更後面的解。這個陣列就是我們一開始說到的表(table)了。如下圖所示:
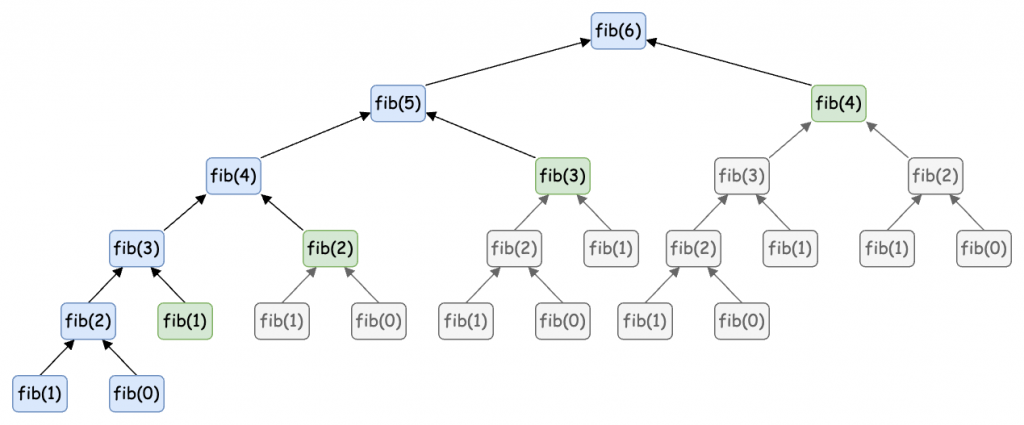
fib(0)、fib(1)、fib(2) 的值(也可以只初始化 fib(0)、fib(1))fib(1) 與 fib(2) 的值得到 fib(3)
fib(n) 的值實作程式碼如下:
function fib(n) {
const table = [0, 1, 1]; // dp table
for (let i = 3; i <= n; i++) {
table[i] = table[i - 1] + table[i - 2]; // fill the table
}
return table[n];
}
現在讓我們來總結一下 DP 的套路。首先,我們有一些起始資料,可以直接放入表中,table[i] 代表著狀態 i 對應子問題的解,例如費氏數列一開始是 [0, 1],接著找到變數,在這裡是 n,並且我們知道從 n = 3 開始 fib(n) 值會是 fib(n - 1) 加上 fib(n-2)。這個變化可以透過方法描述出來,這個方法就是狀態轉換方程:
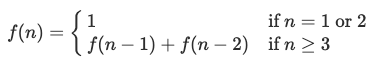
我們需要仔細根據 0、1、2 這幾項的初始解來找規律。又由於動態規劃可以透過無後效性來最佳化效能,回到這題我們可以發現,其實我們只需要保存前兩項的值就可以了,到了第 4 項時,第 1 項的值已經沒用了,所以我們可以用兩個變數來保存前兩項的值,這樣空間複雜度就從 O(n) 降到 O(1) 了。實作程式碼如下:
function fib2(n) {
let a = 0;
let b = 1;
if (n === 0) return a;
for (let i = 2; i <= n; i++) {
const c = a + b;
a = b;
b = c;
}
return b;
}
讓我們打鐵趁熱,來看一個經典的動態規劃題目:Coin Change。
這題的原題為 322. Coin Change,題目如下:
給你一個整數陣列 coins 表示不同面額的硬幣,另給一個整數 amount 表示總金額,問你最少需要多少個硬幣來組成這個金額,如果無法組成,則回傳 -1。
例如有三種硬幣,幣值分別是 1、2、5,總金額為 11,那麼最少需要 3 枚硬幣來組成,即 11 = 5 + 5 + 1。
input: coins = [1, 2, 5], amount = 11
output: 3
explanation: 11 = 5 + 5 + 1
這題很容易讓人直接使用 greedy 來解,優先使用最大面額去除掉總金額,得到個數後再用其他面額去處理餘數。但這樣做很容易得到無解的錯誤結果。我們還是遵循動態規劃的要點,先找出變數,題目中的總金額是不明確的,它需要從外部去傳入,另外硬幣種類可能是 3 也可能是 6,因此它是一個變數。然後我們根據一些邊界值 (0, 1, -1) 來尋找規律,當總金額為 0 時,那麼硬幣數肯定是 0。如果不為 0,那麼至少會有一枚硬幣,它可能是 1、2 或 5 的其中一個,並且它接近總額但不能大於總額,於是問題變成當總額為 amount - coin[i] 時,最少需要多少枚硬幣,這就是硬幣數最少的重疊子問題。
規律公式如下:
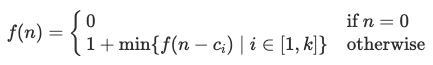
k 為硬幣種類數量,
為第 i 種硬幣的面額。
第二個式子不太好理解,它其實是一個迴圈,在迴圈中不斷呼叫自己找出最小值。不過這裡的 min 只有一個參數,我們可以在程式中新增另一個參數預設是 Infinity,具體程式碼如下:
function coinChange(coins, amount) {
if (amount === 0) return 0;
let ans = Infinity;
for (const coin of coins) {
console.log('TEST');
if (coin <= amount) {
const count = coinChange(coins, amount - coin);
if (count !== -1) {
ans = Math.min(ans, count + 1);
}
}
}
return ans === Infinity ? -1 : ans;
}
console.log(coinChange([1, 2, 5], 11)); // 3
在上面的實作中,實際去跑一下 coinChange([1, 2, 5], 11) 會發現 console.log('TEST') 被打了 927 次才得出 3 這個結果。
因此我們按照之前的方式,使用一個 cache 來改善效能,實作如下:
function coinChange(coins, amount) {
const cache = new Array(amount + 1).fill(Infinity);
cache[0] = 0;
function _coinChange(coins, amount) {
if (cache[amount] !== Infinity) return cache[amount];
let ans = Infinity;
for (const coin of coins) {
if (amount >= coin) {
console.log('TEST');
const count = _coinChange(coins, amount - coin);
if (count !== -1) {
ans = Math.min(ans, count + 1);
}
}
}
cache[amount] = ans === Infinity ? -1 : ans;
return cache[amount];
}
return _coinChange(coins, amount);
}
這次你會發現 console.log('TEST') 已經減少到 28 次了。
最後我們再來改成 bottom-up 的方式。我們需要跑迴圈去填表,那麼 i 要從哪到哪呢?我們已經知道 0 的情況,現在要求 amount 的解,因此 i 從 1 到 amount。也就是:
function coinChange2(coins, amount) {
// 因為是從 0 ~ n 所以 table 長度為 n + 1,並且初始化為 Infinity
const table = new Array(amount + 1).fill(Infinity);
table[0] = 0;
for (let i = 1; i <= amount; i++) {
for (const coin of coins) {
if (i < coin) continue;
// ...
}
}
// ...
}
然後在迴圈裡面,我們利用 table 來取值,替代掉剛才的傳參跑遞迴的方式,剛才的參數是 amount - coin,現在是 table[amount - coin]。
接下來我們要處理 ans = Math.min(ans, count + 1),這裡的 count 其實就是 table[amount - coin]。那 ans 呢?它代表最終解,當 i = amount 時,ans = table[i]。因此我們可以把 ans 改成 table[i],所以可以寫成這樣:
function coinChange2(coins, amount) {
const table = new Array(amount + 1).fill(Infinity);
table[0] = 0;
for (let i = 1; i <= amount; i++) {
for (const coin of coins) {
if (i < coin) continue;
table[i] = Math.min(table[i], table[i - coin] + 1);
}
}
// ...
}
最後是處理無解的情況,如果 table[amount] 還是 Infinity,那就代表無解,回傳 -1。最後的程式碼如下:
function coinChange2(coins, amount) {
// 通常 table 也會被取成 dp
const table = new Array(amount + 1).fill(Infinity);
table[0] = 0;
for (let i = 1; i <= amount; i++) {
for (const coin of coins) {
if (i < coin) continue;
table[i] = Math.min(table[i], table[i - coin] + 1);
}
}
return table[amount] === Infinity ? -1 : table[amount];
}
今天介紹了動態規劃的概念,然後看了兩道經典的動態規劃題目,它的基本思想就是將一個大問題拆成多個子問題,然後將子問題的解保存起來,最後再根據子問題的解推導出大問題的解。但是要注意的是,不是所有遞迴將大問題拆成小問題的情況都可以用動態規劃來解決,例如 merge sort,因為它的子問題是不重複的,每個子陣列都要各自排序,所以這種情況只是單純的分治法,不是動態規劃。
