【動態規劃】Dynamic Programming (2)

2023 iThome 鐵人賽

DAY 29

Software Development

那些前端不用會，但是可以會的資料結構與演算法系列第 29 篇

15th鐵人賽動態規劃 dynamic programming

綿羊

團隊不知道我能不能頂住

2023-10-14 21:45:37

398 瀏覽

分享至

本文同步更新於個人網站中，有更好的排版和程式碼區塊 highlighting 支援。

接續昨天的文章，今天我們繼續來練習動態規劃的題目，熟悉一下動態規劃的解題思路。

爬樓梯 Climbing Stairs

這題的原題為 70. Climbing Stairs，題目如下：假設你正在爬樓梯。需要 n 階你才能到達樓頂，每次你可以爬 1 或 2 個台階。你有多少種不同的方法可以爬到樓頂呢？（1 <= n <= 45）

例如：

給定 n = 2，回傳 2，因為有兩種方法可以爬到樓頂。

1 階 + 1 階
2 階

給定 n = 3，回傳 3，因為有三種方法可以爬到樓頂。

1 階 + 1 階 + 1 階
1 階 + 2 階
2 階 + 1 階

思路：我們可以先從範例觀察一下，dp[1] = 1, dp[2] = 2, dp[3] = dp[1] + dp[2] = 3。接下來確認一下 dp[4] 的值，有 [1,1,1,1], [1,1,2], [1,2,1], [2,1,1], [2,2] 這 5 種組合，然後我們發現 dp[4] = dp[3] + dp[2]。這樣我們就可以推論出狀態轉移方程：

$f(n) = \begin{cases} 1 & \text{if } n = 1 \\ 2 & \text{if } n = 2 \\ f(n - 1) + f(n - 2) & \text{if } n \geq 3 \end{cases}$

知道規律後就可以利用動態規劃來解題了，實作程式碼如下：

function climbStairs(n) {
  const dp = [0, 1, 2];
  for (let i = 3; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
}

可以發現這題的解法跟費氏數列很像，但是不同的是費氏數列的初始值是 [0, 1]，而這題的初始值是 [0, 1, 2]，但是它們之後的規律都是一樣的。

最長不下降子序列 Longest Non-decreasing Subsequence

有一個由 n (n <= 1 <= 200) 個整數組成的數列，標記為： $a_1, a_2, ..., a_n$ 。請你從中找出一個最長的不下降子序列，也就是說找出一個最長的整數序列 $i_1, i_2, ..., i_k$ ，使得對於任意的 j (1 <= j <= k - 1)，都滿足 $i_j < i_{j + 1}$ 且 $a_{i_j} \leq a_{i_{j + 1}}$ 。

例如：[1, 2, 3, -9, 3, 9, 0, 11]，它的最長不下降子序列為 [1, 2, 3, 3, 9, 11]。

暴力遞迴

比較直觀的想法會是窮舉出所有的不下降子序列，然後找出最長的那個。我們可以固定序列的最後一項數字，例如 array 的最後一個是 11，我們就先以 11 當作序列結尾，往前找到 0、9、3、-9、3、2、1 都可以接上去 11，依此類推繼續找下去，得出以 11 為結尾的最長序列後再接著去找以 9 為結尾的最長序列，一路找下去，最後找出最長的序列。

我們將思路轉為程式碼，實作如下：

function longestNonDecreasingSequence(array) {
  const allSubsequences = [];

  for (let i = array.length - 1; i >= 0; i--) {
    allSubsequences.push(findLongestFromIndex(array, i));
  }

  return findLongestSubsequence(allSubsequences).reverse();
}

const findLongestSubsequence = (array) => {
  return array.reduce((acc, subsequence) => {
    if (subsequence.length > acc.length) {
      return subsequence;
    }
    return acc;
  }, []);
};

const findLongestFromIndex = (array, index) => {
  if (index === 0) {
    return [array[0]];
  }

  const currentNumber = array[index];
  const subsequences = [];

  for (let i = index - 1; i >= 0; i--) {
    if (array[i] <= currentNumber) {
      subsequences.push(findLongestFromIndex(array, i));
    }
  }

  if (subsequences.length === 0) {
    return [currentNumber];
  }

  const longestSubsequence = findLongestSubsequence(subsequences);

  return [currentNumber, ...longestSubsequence];
};

Memoization

但仔細觀察後我們可以注意到我們在遞迴的過程中，有很多重複的計算，例如：[1, 2, 3, -9, 3, 9, 0, 11]，當我們計算以 11 為結尾的最長序列時，會先計算以 9 為結尾的最長序列，而當我們計算以 9 為結尾的最長序列時，又會先計算以 3 為結尾的最長序列，以此類推。我們可以用一個快取記下計算過的結果，程式碼如下：

function longestNonDecreasingSequence(array) {
  const memo = {};
  const allSubsequences = [];

  for (let i = array.length - 1; i >= 0; i--) {
    allSubsequences.push(findLongestFromIndex(array, i, memo));
  }

  return findLongestSubsequence(allSubsequences).reverse();
}

const findLongestSubsequence = (array) => {
  return array.reduce((acc, subsequence) => {
    if (subsequence.length > acc.length) {
      return subsequence;
    }
    return acc;
  }, []);
};

const findLongestFromIndex = (array, index, memo) => {
  if (memo[index] !== undefined) {
    return memo[index];
  }

  if (index === 0) {
    return [array[0]];
  }

  const currentNumber = array[index];
  const subsequences = [];

  for (let i = index - 1; i >= 0; i--) {
    if (array[i] <= currentNumber) {
      subsequences.push(findLongestFromIndex(array, i, memo));
    }
  }

  let longestSubsequence = [];
  if (subsequences.length > 0) {
    longestSubsequence = findLongestSubsequence(subsequences);
  }

  memo[index] = [currentNumber, ...longestSubsequence];

  return memo[index];
};

動態規劃

思路：我們建立一個 table，長度等於原數列長度，table[i] 表示以 array[i] 為結束的非下降子序列的長度。一開始它們的值都是 1，可以參考下表。我們分別用 [4]、[1,3]、[3,1] 和 [1,2,3] 這些總長為 1、2、3 的陣列來推論規律。

array	table initStatus	table lastStatus
`[4]`	`[1]`	`[1]`
`[1,3]`	`[1,1]` j=0, i=1	`[1,2]`
`[3,1]`	`[1,1]` j=0, i=1	`[1,1]`
`[1,2,3]`	`[1,1,1]`	`[1,2,3]`

如果 array[i] >= array[j](j < i)，那麼 table[i] = Math.max(table[i], table[j] + 1)。

因此 table 中的元素隨著索引的遞增，其值即便不加 1 也不會變小，就像一個台階一樣不斷往上累加 1。

又由於 table[i] 的值是透過 0 ~ i 的子陣列推導出來的，因此我們可以用一個雙層迴圈來填表，i 跑整個陣列，j 跑 0 ~ i 的子陣列。實作程式碼如下：

function longestNonDecreasingSequence(array) {
  const dp = new Array(array.length).fill(1);
  let max = 1;
  let maxIndex = 0;

  for (let i = 1; i < array.length; i++) {
    for (let j = 0; j < i; j++) {
      const current = array[i];
      const previous = array[j];

      if (current >= previous && dp[i] < dp[j] + 1) {
        dp[i] = dp[j] + 1;

        if (max < dp[i]) {
          max = dp[i];
          maxIndex = i;
        }
      }
    }
  }

  const result = [array[maxIndex]];
  let m = max;
  let i = maxIndex - 1; // 從最後一個往前找
  while (m > 1) {
    // 相鄰的 dp[i] 都是等差或是相差 1
    if (dp[i] === m - 1 && array[i] <= array[maxIndex]) {
      result.unshift(array[i]);
      maxIndex = i;
      m--;
    }
    i--;
  }

  return result;
}

這個問題其實就是最長遞增子序列（Longest Increasing Subsequence, LIS）的變形，多了一個等於的條件。有興趣的讀者可以參考 300. Longest Increasing Subsequence。

最長共同子序列 Longest Common Subsequence

給你兩個字串，求解這兩個字串的最長共同子序列（Longest Common Subsequence, LCS）的長度。例如：abcde 與 ace 的 LCS 為 ace，長度為 3。

LCS 是一個很實用的問題，它可以是不連續的。它可以用在描述兩段文字之間的“相似度”，也就是雷同程度，進而去判斷是否為抄襲。對一段文字進行修改時，計算修改前後文字的 LCS，將除此子序列外的部分提取出來，用這個方式來判斷修改的部分，往往十分準確。

暴力遞迴

一開始一樣可以先試著想暴力解要怎麼去解，這題比上一題再難一點，因為多了一個字串，不過我們一樣依循從尾巴開始往前尋找的策略來起手，例如：abcde 與 ace，我們先找出 abcde 的最後一個字母 e 和 ace 的最後一個字母 e，發現它們相同，於是我們把這個 e 扣掉然後接這去找 abcd 和 ac 的 LCS，接著我們又發現 d 與 c 不同，於是我們可以選擇扣掉 d 或是 c，然後再去找 abc 和 ac 的 LCS 和 abcd 和 a 的 LCS，然後選一個最長的，依此類推，直到其中一個字串為空為止。

實作起來會長這樣：

function LCS(str1, str2) {
  const findLCS = (str1, str2, i, j) => {
    if (i < 0 || j < 0) {
      return 0;
    }

    if (str1[i] === str2[j]) {
      // 如果兩個字元相同，則 LCS 長度加 1，然後繼續往前找
      return 1 + findLCS(str1, str2, i - 1, j - 1);
    }

    const option1 = findLCS(str1, str2, i - 1, j); // 從 str1 的前一個字元開始找
    const option2 = findLCS(str1, str2, i, j - 1); // 從 str2 的前一個字元開始找

    return Math.max(option1, option2); // 取最大值
  };

  return findLCS(str1, str2, str1.length - 1, str2.length - 1);
}

不過想當然這樣寫的時間複雜度非常大，用我們系列文專案中的測資下去跑測試會在最後一個情境直接卡住，因此我們需要用動態規劃來解決這個問題。

動態規劃

思路：這題有兩個字串，因此填表用的 table 會變成二維陣列，也就是矩陣。矩陣的橫列表示第一個字串，縱行表示第二個字串，如果某一列與某一行相交的字元相同，我們就填 1，否則就填 0。但這樣點完之後還需要再清點一次，如圖所示：

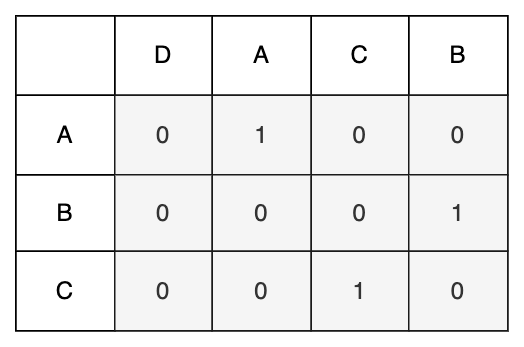
我們繼續來改進一下，如果格子對應的字元相同，那麼它的值就等於左上角格子的值加 1，如果不存在則預設為 0；如果不相同，那麼它的值就等於左邊格子與上面格子取最大值。最後右下角的值就是 LCS 的長度。如下圖所示：

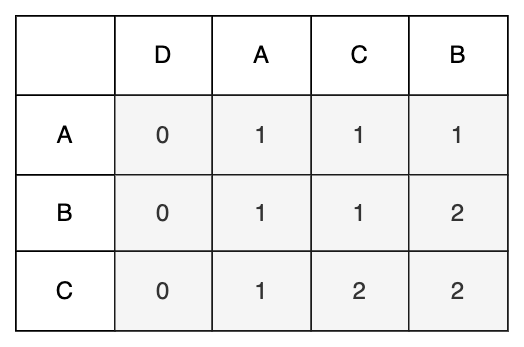
根據上面的規則，我們可以寫出狀態轉移方程：

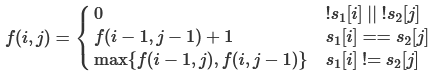
整個轉移的過程如下：

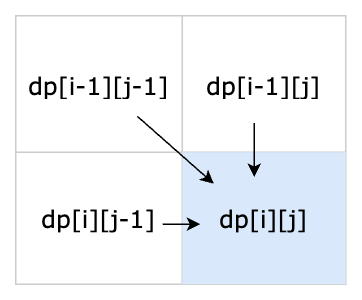
為了避免左上格子不存在的問題，我們有兩種解法：一是將 str1、str2 字串轉換成陣列，然後在陣列前面加上一個空字串，並規定空字串與其他字串比較時，結果永遠是 0；二是在矩陣左側和上方額外新增 1 行與列，並將它們的值都設為 0，效果如下圖所示：

我們用第二種方式來實作，程式碼如下：

function LCS(str1, str2) {
  const m = str1.length;
  const n = str2.length;

  const dp = [new Array(n + 1).fill(0)];

  for (let i = 1; i <= m; i++) {
    dp[i] = [0];
    for (let j = 1; j <= n; j++) {
      if (str1[i - 1] === str2[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1] + 1;
      } else {
        dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
      }
    }
  }

  return dp[m][n];
}

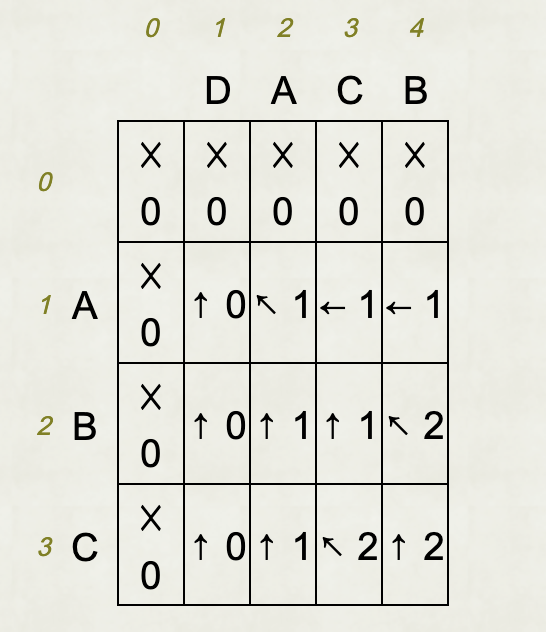
如果我們要實際求出 LCS 字串，可以從右下角開始往左上角找回去，遇到相同的字元就加入結果中，遇到不同的字元就往左或往上找，直到找到左上角為止。我們可以使用一個遞迴函式來實現，程式碼如下：

function printLCS(dp, str1, str2, i, j) {
  if (i === 0 || j === 0) {
    return '';
  }

  if (str1[i - 1] === str2[j - 1]) {
    return printLCS(dp, str1, str2, i - 1, j - 1) + str1[i - 1];
  }

  if (dp[i][j - 1] > dp[i - 1][j]) {
    return printLCS(dp, str1, str2, i, j - 1);
  }

  return printLCS(dp, str1, str2, i - 1, j);
}

function LCS(str1, str2) {
  // 略
  const lcs = printLCS(dp, str1, str2, m, n);
  console.log(lcs);
  return dp[m][n];
}

LCS('DACB', 'ABC'); // AC

背包問題 - 0/1 Knapsack Problem

給定 n 個重量為 $w_1, w_2, ..., w_n$ ，價值為 $v_1, v_2, ..., v_n$ 的物品和一個容量為 capacity 的背包，求如何裝才能在不超過背包承重的情況下，使得背包中物品的總價值最大？

「0/1」的意思是每件物品只能選擇 0 個或 1 個。也就是要嘛就是放進背包，要嘛就是不放進背包。

在介紹 backtracking 時我們就有提到過 0/1 背包問題，我們當時是利用回溯法直接暴力窮舉出所有可能的組合，然後找出最大值，今天我們來看看如何用動態規劃來解決這個問題。

我們可以讓物品編號從 1 開始，陣列索引從 0 開始，因此物品 i 的重量為 w[i - 1]，價值為 v[i - 1]。如下表範例所示：

物品 `i`	重量 `w[i - 1]`	價值 `v[i - 1]`
1	10	50
2	20	120
3	30	150
4	40	210
5	50	240

capacity = 50 時，最佳方案為放入 2、3，總價值為 270。

思路：

第一步：我們要思考每一輪的決策，定義出狀態，進而推導出 dp 表的結構。

對於每個物品來說，不放入背包，背包容量不變；放入背包，背包容量減小。我們把目前物品 $i$ 和剩餘容量 $c$ ，記作 $[i, c]$ 。

狀態 $[i, c]$ 對應的子問題是：在前 $i$ 個物品中選擇，且剩餘背包容量為 $c$ 時，背包中物品的最大價值，記作 $dp[i][c]$ 。

我們要知道的是 $dp[n][capacity]$ ，因此需要一個 $(n + 1) * (capacity + 1)$ 的矩陣來存放子問題的解。

第二步：找出最佳子結構，推導出狀態轉移式

當我們做出物品 $i$ 的決策後，剩餘的是前 $i - 1$ 個物品的決策，有兩種情況：

不放入物品 $i$ ：背包容量不變，狀態變為 $[i - 1, c]$ 。
放入物品 $i$ ：背包容量減少 $w[i - 1]$ ，價值增加 $v[i - 1]$ ，狀態變為 $[i - 1, c - w[i - 1]]$ 。

我們的決策就是在這兩種情況中選擇價值最大的那個，因此狀態轉移方程為：

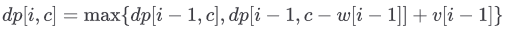
這邊要注意若目前物品 $i$ 的重量大於剩餘容量 $c$ ，則必定不能放入物品 $i$ 。

第三步：確定邊界條件和狀態轉移順序

當沒有物品或是無剩餘空間時，最大價值為 0，即 $dp[0, c] = dp[i, 0] = 0$ 。

狀態 $[i, c]$ 從上方的 $[i - 1, c]$ 或是左上方的 $[i - 1, c - w[i - 1]]$ 轉移而來，因此我們需要先計算出上方的狀態，再計算左上方的狀態，因此我們的狀態轉移順序為：先計算 dp[1, 1], dp[1, 2], ..., dp[1, capacity]，再計算 dp[2, 1], dp[2, 2], ..., dp[2, capacity]，以此類推。

實作程式碼如下：

function knapsack01(w, v, capacity) {
  const n = w.length;

  // 初始化 dp 表
  const dp = new Array(n + 1).fill(0).map(() => new Array(capacity + 1).fill(0));

  // 填表
  for (let i = 1; i <= n; i++) {
    for (let c = 1; c <= capacity; c++) {
      if (w[i - 1] > c) {
        // 目前物品超過背包容量，不放入背包
        dp[i][c] = dp[i - 1][c];
      } else {
        // 選擇放或不放，取最大值
        dp[i][c] = Math.max(dp[i - 1][c], dp[i - 1][c - w[i - 1]] + v[i - 1]);
      }
    }
  }

  return dp[n][capacity];
}

總結

動態規劃不像回溯法那樣有特定的套路，雖然我們可以針對可變的部分抽取出狀態，但這些狀態需要結合填表法才能找到真正的意義。此外關於狀態轉移式，有的題目已經給出前幾步的結果，你可以輕鬆地推論出來；有的題目就比較難，這些都需要透過練習去累積經驗，在一開始我們可以先試著找出如何暴力解，然後再嘗試用動態規劃來解決，這樣會比較容易理解。