終於來到三分之一了，但是已經沒有庫存了，要趕緊進度摟

什麼是樹

樹(Tree)是一種階層式(Hierarchical)架構，由一個或多個節點(node)以及連接這些節點的邊(edge)所構成，模擬了自然界中樹的結構。

樹的優勢

樹資料結構之所以被廣泛使用，原因如下：

1. 組織和層次化數據：樹允許您以分層方式組織和表示數據。這對於模擬層次結構的情況非常有用，如文件系統中的目錄結構或組織中的部門層次。
2. 快速查找和插入：樹提供了高效的數據檢索方法，特別是二元搜尋樹(Binary Search Tree)，可以在較快的時間內查找和插入數據，這對於搜索和更新操作很重要。
3. 排序：樹資料結構可以用於高效的排序操作，例如二元搜尋樹(Binary Search Tree)的中序遍歷可以按升序檢索數據。
4. 動態資料：樹是動態資料結構，它們可以根據需要成長和縮小，而不需要預先指定大小。
5. 高效的插入和刪除：樹提供了用於插入和刪除資料的高效演算法，這在許多需要頻繁添加或刪除資料的應用程式中非常重要。例如，二元搜尋樹(Binary Search Tree)中的插入和刪除操作通常具有O(log n)的時間複雜度。
6. 易於實現：樹相對容易實現，特別是與其他複雜的資料結構，如圖相比。
7. 表達關係： 樹資料結構用於表示和表達事物之間的關係。例如，家譜可以使用樹來表達家庭成員之間的關係。
8. 遞歸操作： 樹資料結構在遞歸操作中特別有用，因為它們使得問題可以自然地分解成子問題，從而簡化了算法的實現。

樹的基本術語(terminology)

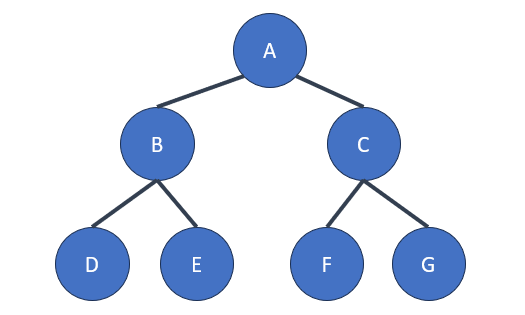
以下是樹的一些基本概念和特點：

• 根節點（Root）：樹的頂部結點，所有其他節點都以某種方式與根節點相關聯。 (圖中的根結點是A)
• 節點（Node）：樹中的每個元素都稱為一個節點。(在示例圖中，有七個結點，分別為A、B、C、D、E、F和G)
• 邊（Edge）：邊是連接樹中不同節點的線。它表示節點之間的關係。(圖中，A到B的連接線即為一條邊)
• 內部節點(internal node): 有子結點的節點被稱為內部節點。(在示例圖中，A、B和C都是內部節點)
• 葉節點(Leaf Node)：在樹結構中，沒有子節點的節點被稱為葉節點。葉節點位於樹的最底層。(在示例圖中，D、E、F和G都是葉節點)
• 父節點(Parent)：每個節點都可以有一個父節點，即直接連接到它的上一層節點。
  例如：圖中A,B,C
  A為 B,C 的父節點;
  B為D,E的父節點;
  C為F,G的父節點
• 子節點（Child Node）：與父結點相關聯的結點被稱為子節點，形成層次結構。
  例如：在示例圖中，A,B,C
  A 的子節點為B,C;
  B的子節點為D,E;
  C的子節點為F,G
• 深度（Depth）：一個節點到根節點的路徑上的邊的數量，根節點的深度為0。(在示例圖中，B的深度是1，D的深度是2)
• 高度（Height）：從該節點到葉節點的最長向下路徑的長度。(圖中A的高度是2，因為最長向下路徑是A到D or E or F or G)
• 分支（Branch）：一個節點和它的所有子節點構成了一個分支。(例如圖中A和其子結點B、C構成了兩個分支)
• 子樹（Subtree）：一個節點及其所有後代構成了一個子樹，可以視為樹的一部分。(在示例圖中，以B為根的子樹包括B、D和E)
• 兄弟(Sibling): 有相同父結點的所有子節點互稱兄弟。(在示例圖中，B和C是兄弟節點)
• 鄰居(Neighbor): 在同一層次的兄弟節點。(在示例圖中，B和C是鄰居節點;D,E,F,G是鄰居節點)
• 祖先(Ancestor): 一個節點的所有前代節點。(在示例圖中，B的祖先包括A)
• 後裔(Descendant): 一個節點的所有後代節點。(在示例圖中，A的後裔包括B、C、D、E、F和G)
• 森林(Forest) : 一組一棵或多棵不相交的樹。如果有多個獨立的樹結構，它們組成了一個森林。
• 分支度(Degree) : 對於給定節點，其子節點的數量。葉子的度數必然為零。(在示例圖中，A的分支度是2，B的分支度是2，D的分支度是0)
• 樹的度(Degree of tree)：樹中節點的最大度數。(在示例圖中，樹的度是2，因為沒有節點的度超過2)
• 距離(Distance)：兩個節點之間最短路徑的邊數。(在示例圖中，A到G的距離是2)
• 層級(Level)表示節點所處的層次或深度。(在示例圖中，A處於第0層，B和C處於第1層)
• 寬度(Width)：某層次中的節點數。(在示例圖中，第1層的寬度是2，第2層的寬度是4)
• 範圍(Breadth)：葉節點的數量。(在示例圖中，樹的範圍是4)
• 有序樹(Ordered tree)：節點之間有明確的順序。
• 有向樹(Directed Tree)每條邊都有一個關聯的方向，通常是從父節點到子節點，並且有一個指定的根節點，從該根節點可以透過沿著有向邊到達所有其他節點。
• 樹的大小(Size of a tree)：樹中包含的節點總數。(在示例圖中，樹的大小是7)
• 非終端節點（Non-terminal Nodes）：除了葉節點之 外的其它節點稱為非終端節點。

樹結構被廣泛應用，用於組織和操作數據，解決各種問題。由於不同種類的樹結構具有不同的特點，可根據特定需求選擇合適的樹結構。

樹的表示方式

樹(Tree)可以通過多種方式來表示，其中兩種常見的方式包含隱含式（Implicit）、外顯式(Explicit)。

1. 外顯式表達(Explicit Representation)
   樹的結構和所有相關信息都被明確地存儲在數據結構中。

   • 我們使用指針（pointers）來表示節點之間的連接關係。一個節點如果有k個子節點，就會有k個指針。
   • 為了簡化結構，通常設計成每個節點都有相同數量的指針，這個數量是樹中最大子節點數量。

2. 隱含式表達（Implicit Representation）
   樹的結構和關係是通過某種算法或規則來推導或計算的，而不是直接存儲所有節點和邊的信息。
   這種表達方式通常用於特定的數據結構或演算法中，以節省空間和提高效率。例如，對於平衡二叉搜索樹（如紅黑樹），樹的結構和平衡性是通過紅黑節點的規則來確定的，而不需要額外的指針來表示。

   總而言之，外顯式表達提供了直觀的方式來訪問和操作樹的結構，但可能需要更多的存儲空間。隱含式表達節省了存儲空間，但操作可能需要更多的計算。

常見的樹

1. Binary Tree
2. Binary Search Tree
3. Heap
4. Self-Balancing Binary Search Trees

今天就先到這裡，我會在之後一一說明。

不要害怕面對，因為事實上，面對有時候並沒有那麼可怕。