Hi大家好，今天要繼續介紹2D動態規劃裡面很經典的問題，你會發現有很多動態規劃的問題都有相似的pattern。

Longest Common Subsequence

首先，什麼是subsequence?
Ans:是input list(array, string)的子集，但是保有原本input list的元素的相對順序。例如：s1 = "jason"，"jsn"是subsequence，但是"ajs"不是。所以suqsequence不需要是連續的元素，只需要相對順序是對的。

現在讓我們看看題目敘述：
有兩個字串，s1, s2。找出這兩個字串共同的最長subsquence。

分析：
既然我們都說要利用動態規劃來解決問題了，那我們的目標就是要將問題切割出子問題，如果我們可以發現問題和子問題之間的關係，就有辦法利用遞迴搭配Memoization去解決問題。

假設分別有兩個指標指著這兩個字串，我們可以發現如果剛好指著的字元都是一樣的，代表現在的common subsequence是1，同時我們可以把指標往後移，也就是說前一個字元已經不用管了，代表我們把這兩個字串的長度都縮減1：他們成為了原本字串的子字串。

這是一個很好的開始，我們再把剛剛的假設情況整理得更清晰。
情況1：

s1[i] == s2[j] => 1 + LCS(s1, s2, i+1, j+1)

這樣子就寫出了某種情況下的遞迴關係式了。我們現在只需要面對子問題：s[i+1:], s[j+1:]。
如果有剛好兩個指標指著同樣字元的情況，那勢必會有相反的情況。

情況2：

s1[i] != s2[j]

我們希望可以一直出現情況1，但是我們不知道現在要移動哪一個指標才會在那之後又出現情況1。所以只能所有狀況都嘗試，也就是窮舉。

max(LCS(s1, s2, i + 1, j), LCS(s1, s2, i, j + 1))

現在我們分析完他所有的情況後，就可以把他們畫成決策樹了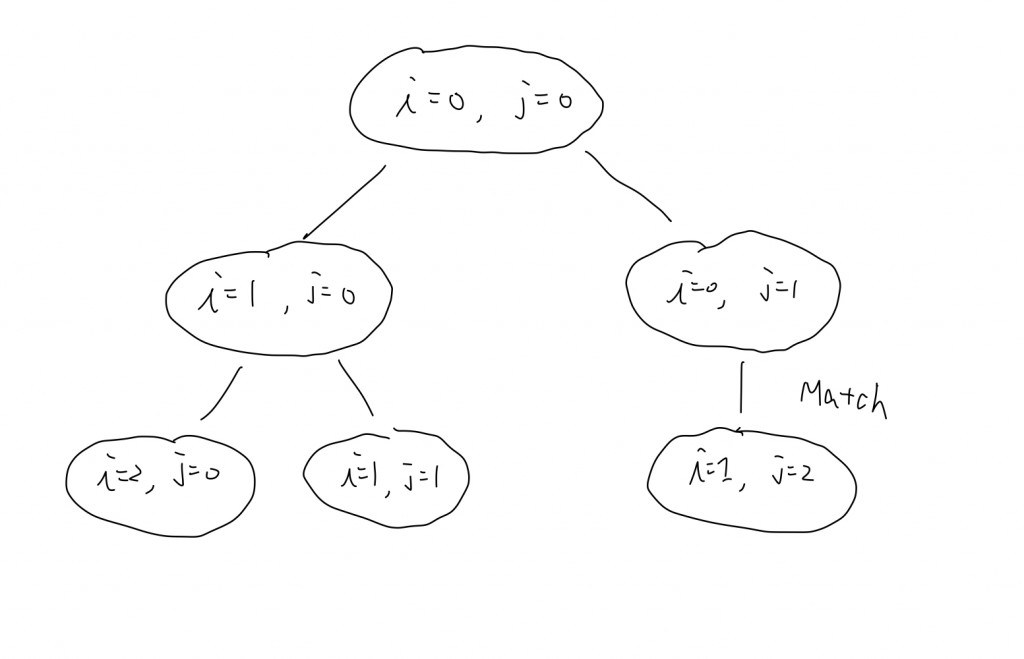

情況1時，我們只有一種選擇；情況2時我們有兩種。

有了決策樹後，幾乎就能確定可以以Memoization的方式解決問題了。

# Time: O(n * m), Space: O(n + m)
def memoization(s1, s2):
    N, M = len(s1), len(s2)
    cache = [[-1] * M for _ in range(N)]
    return memoHelper(s1, s2, 0, 0, cache)

def memoHelper(s1, s2, i1, i2, cache):
    if i1 == len(s1) or i2 == len(s2):
        return 0
    if cache[i1][i2] != -1:
        return cache[i1][i2]

    if s1[i1] == s2[i2]:
        cache[i1][i2] = 1 + memoHelper(s1, s2, i1 + 1, i2 + 1, cache)
    else:
        cache[i1][i2] = max(memoHelper(s1, s2, i1 + 1, i2, cache),
                memoHelper(s1, s2, i1, i2 + 1, cache))
    return cache[i1][i2]

現在我們可以進一步去看如何以Bottom up的方式來解決問題。我們的核心概念沒有變依舊是那兩種情況。

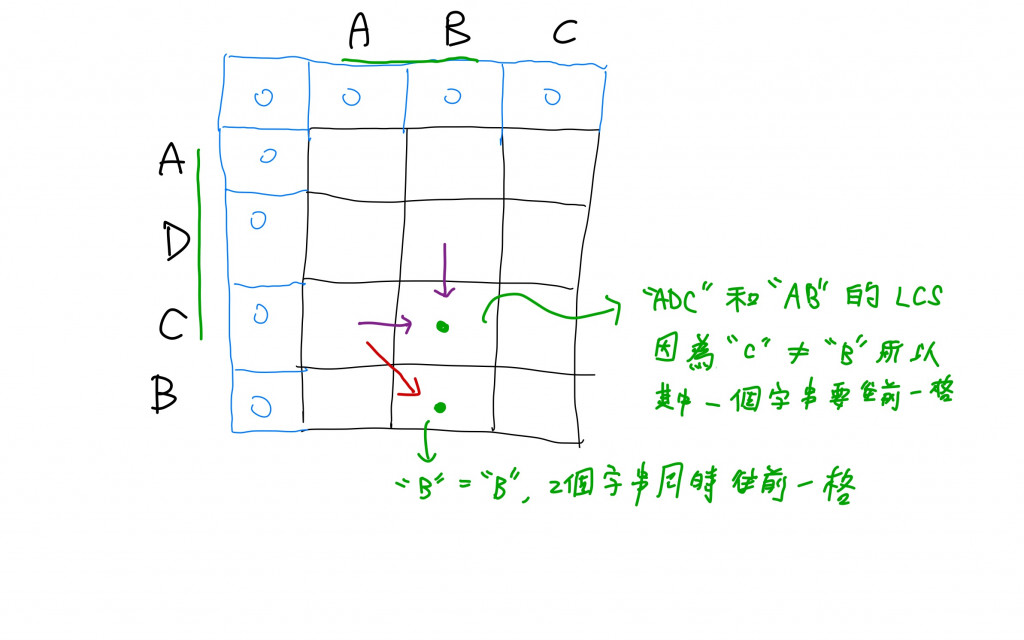
以Bottom up解題時會發現這就是妥妥的2D動態規劃問題。我們需要讓我們的2D陣列多一行一列（藍色的部分），這樣程式才能運行下去。

# Time: O(n * m), Space: O(n + m)
def dp(s1, s2):
    N, M = len(s1), len(s2)
    dp = [[0] * (M+1) for _ in range(N+1)]

    for i in range(N):
        for j in range(M):
            if s1[i] == s2[j]:
                dp[i+1][j+1] = 1 + dp[i][j]
            else:
                dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j])
    return dp[N][M]

我們可以繼續優化空間複雜度，從程式碼中我們可以發現，我們不需要一開始就給定一個二維陣列。因為每次在計算時，我們只會用到當下的一維陣列和上一輪的一維陣列（以上圖為例：第一輪我們以"A"和"ABC"來做比較，我們只需要一個長度為4的一維陣列。下一輪是"D"和"ABC"的比較，當"D"發現自己無法和比較的字元匹配時，會去看自己的一維陣列的左邊，以及上一輪一維陣列同行的位置，尋找比較大的值。依此類推...）

# Time: O(n * m), Space: O(m)
def optimizedDp(s1, s2):
    N, M = len(s1), len(s2)
    dp = [0] * (M + 1)

    for i in range(N):
        curRow = [0] * (M + 1)
        for j in range(M):
            if s1[i] == s2[j]:
                curRow[j+1] = 1 + dp[j]
            else:
                curRow[j+1] = max(dp[j + 1], curRow[j])
        dp = curRow
    return dp[M]

這是個第一次看到需要花時間去消化的問題。最好是自己畫圖才能比較好理解。之後就可以利用這個pattern去解相似的問題了。