今天要來分享的是貪婪演算法。這個演算法除了一些經典的問題可以讓人知道會使用到這個策略外（之後會介紹）最難的地方，我認為是如何判斷題目是否可以利用貪婪演算法來解題。

使用時機

1. 每一次做的決定（運算）可以讓問題的規模變小，而且可以被認定是最佳的選擇
2. 和動態規劃問題不同的地方在於，我們不需要去尋求子問題之間的關係、不需要去利用子問題所保存的最佳解：「子問題不重疊」

「子問題不重疊」這句話是貪婪演算法的核心，我們不需要去利用到子問題的答案。這樣說可能還是有點抽象，所以接下來就直接來看題目。

Leetcode 55. Jump Game

題目敘述：有一個整數的陣列，裡面每個元素的值代表可以一次最多跳幾格。判斷我們是否能從起點（index等於0）跳到陣列的最後一個index。

Example

Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

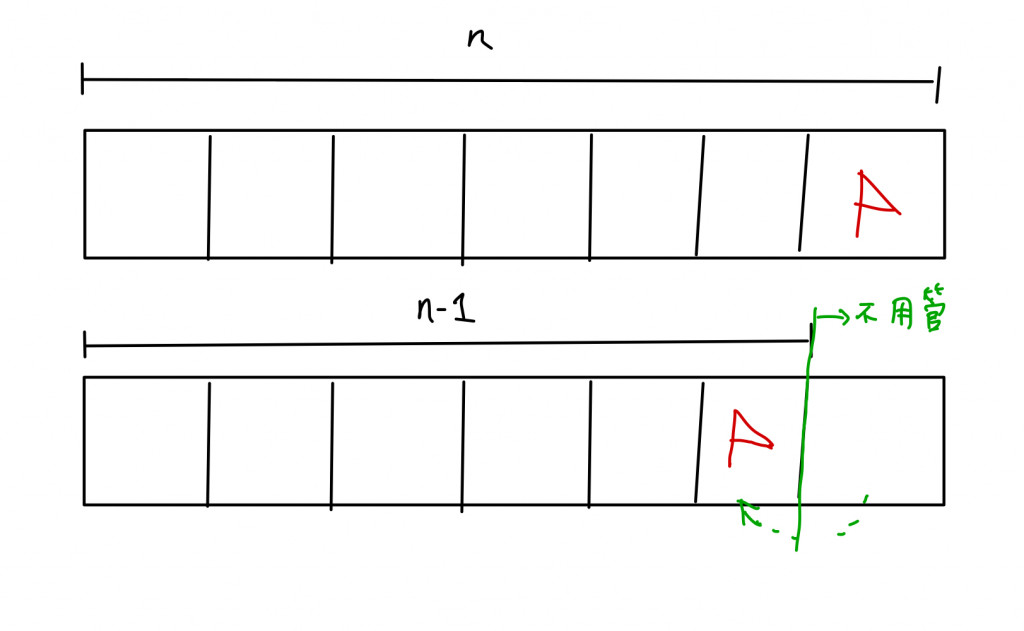
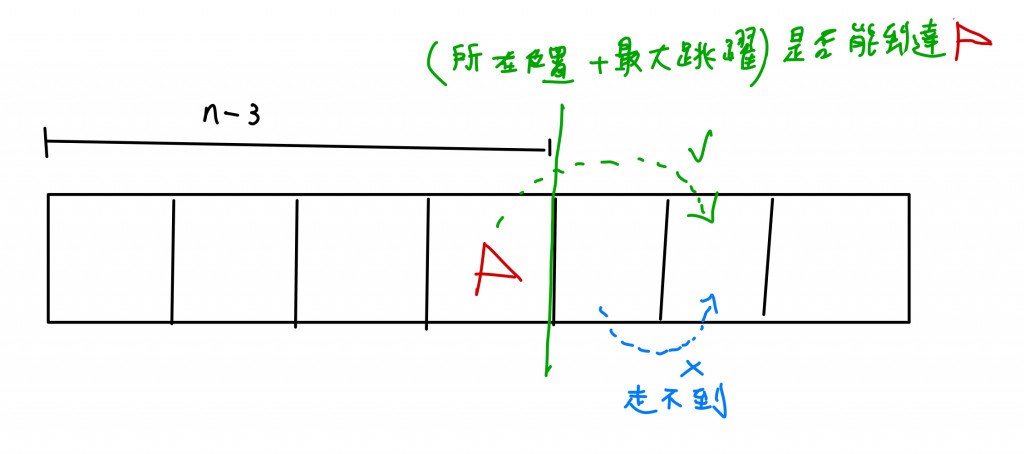
分析：這個題目可以使用動態規劃去解決，但是時間複雜度較高。如果嘗試使用貪婪演算法解題的話，我們要試圖去撿小問題的規模：比如說我們在最後一個index插著一面旗子，如果我可以從第i個格子最終跳躍到旗子那格，那我們現在要考慮的就是如何從起點到達第i個格子，所以我們把旗子移到第i個格子，這樣就成功減小問題的大小，並且題目只問是否能到達插著旗子的地方，所以當我們移動旗子的方式可以視為最佳選擇。

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        # 如果可以從第i個index走到最後一個index，那我們現在只需要考慮怎麼到達第i個index
        goal = len(nums) - 1
        for i in range(len(nums) - 2, -1, -1):
            if nums[i] + i >= goal:
                goal = i
        
        return True if goal <= 0 else False

Follow Up Leetcode 45. Jump Game II

敘述：現在題目要求到達最後一格圖中可以經過的其他index要最少數目。

Example

Input: nums = [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.

分析：我們可以利用上一題延續下來的想法，當原本旗子從最後一格往前移，最多可以移到哪一格。然後在以那一格為新的終點，繼續把旗子盡可能地往前移。不過這樣的時間複雜度是O(n^2)。

class Solution:
    def jump(self, nums: List[int]) -> int:
        goal = len(nums) - 1
        count = 0

        while goal != 0:
            tmp = 0
            for i in range(goal - 1, -1, -1):
                if i + nums[i] >= goal:
                    tmp = i
            
            goal = tmp
            count += 1
        
        return count
            

我們可以做得更好。
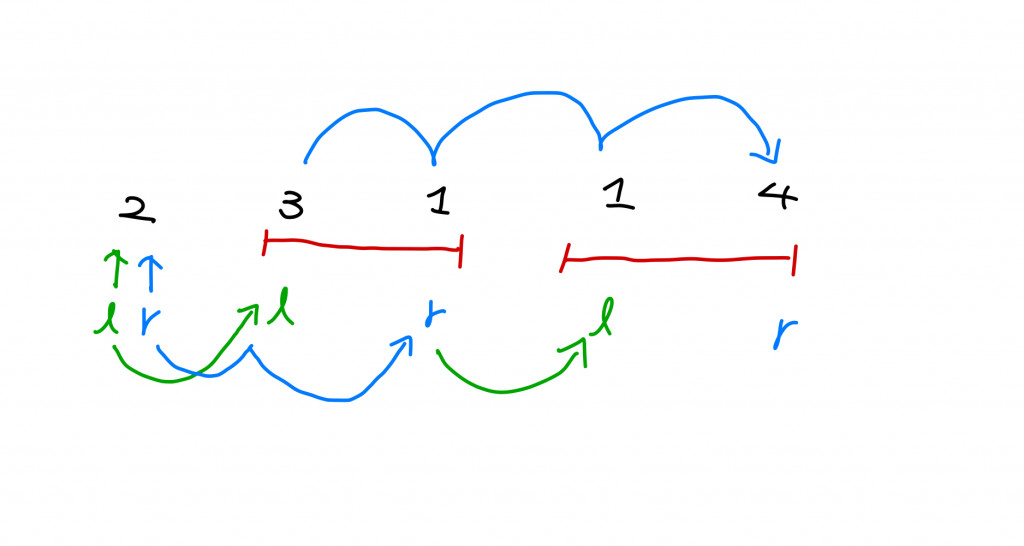
分析2：我們可以利用BFS的概念，從起點開始計算，下一次我們可以走的index有哪些，是一個範圍，所以我們要用兩個指標指著。然後從這個範圍中選取出可以跳到最遠的index，它會是下下一次範圍的上限。

class Solution:
    def jump(self, nums: List[int]) -> int:
        l, r = 0, 0
        res = 0
        while r < (len(nums) - 1):
            maxJump = 0
            for i in range(l, r + 1):
                maxJump = max(maxJump, i + nums[i])
            l = r + 1
            r = maxJump
            res += 1
        return res

如何不燃燒殆盡，每天都維持產能是一件很重要的事情。秘訣或許是從過程中找到樂趣吧。謝謝大家觀看這篇文章。