今天要來繼續分享Topological sort在leetcode上的題目，這個主題的題目沒有easy難度的。只有Medium和Hard，算是不簡單的主題。今天原本是想分享兩個題目，但是有一題卡住了，並且沒有多餘的時間，所以有一題會放在明天和別的主題一起分享。

Leetcode 210. Course Schedule II

題目敘述：input會給一個整數n，代表總共會有編號0- n-1門不同的課程。想要修某些課程會有一些必須先修的課程，完成那些課程才能再修此課程。以[0,1]表示，若想要修編號0的課程需要先修過編號1的課程。input會給一個nested array叫 prerequisites，裡面就是會有剛才提到的這種先修條件（prerequisites[i] = [a, b]）。
找出一個有效的修課程的順序，若找不出來回傳空array。

Example1:

Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
Output: [0,2,1,3]
Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3].

Example2:

Input: numCourses = 1, prerequisites = []
Output: [0]

分析：
一般來說我們會將先修完某某課程(a)，再去修以這門課為先修條件的課程(b)，以a->b來表示。但是題目卻將關係表達反過來，也就是為了修這門課，需要先去修另外一門課。但是這樣對於我們解題是方便的，以Example1來說：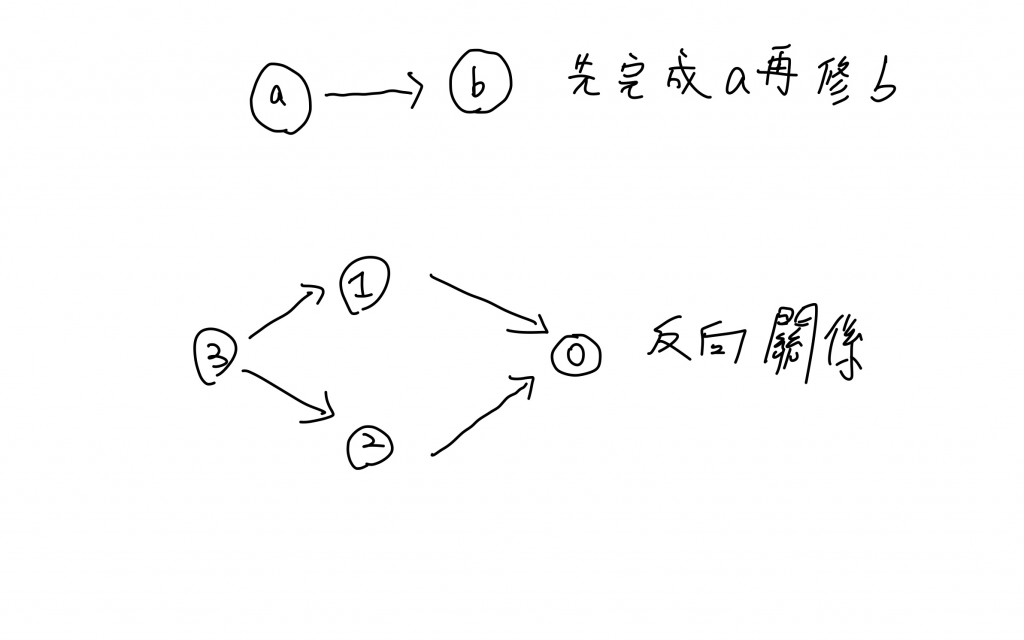

要完成課程3就要先完成課程2和課程1，而要完成這兩門課則須要完成課程0。以這種關係去建構graph，這樣我們在做完post order DFS(Topological sort)後就不必再反轉output的順序了。

我們依序來看會如何Traverse圖上的節點（假設從課程3開始）：
首先紅色的勾勾代表已拜訪過的節點；綠色的代表這條路徑上拜訪過的節點，當這條路徑走到底，即沒有任何可以拜訪卻尚未拜訪的節點時，我們就會返回，這時候要將綠色的勾勾取消掉，因為這只是為了確認路徑是否會成為迴圈所使用的。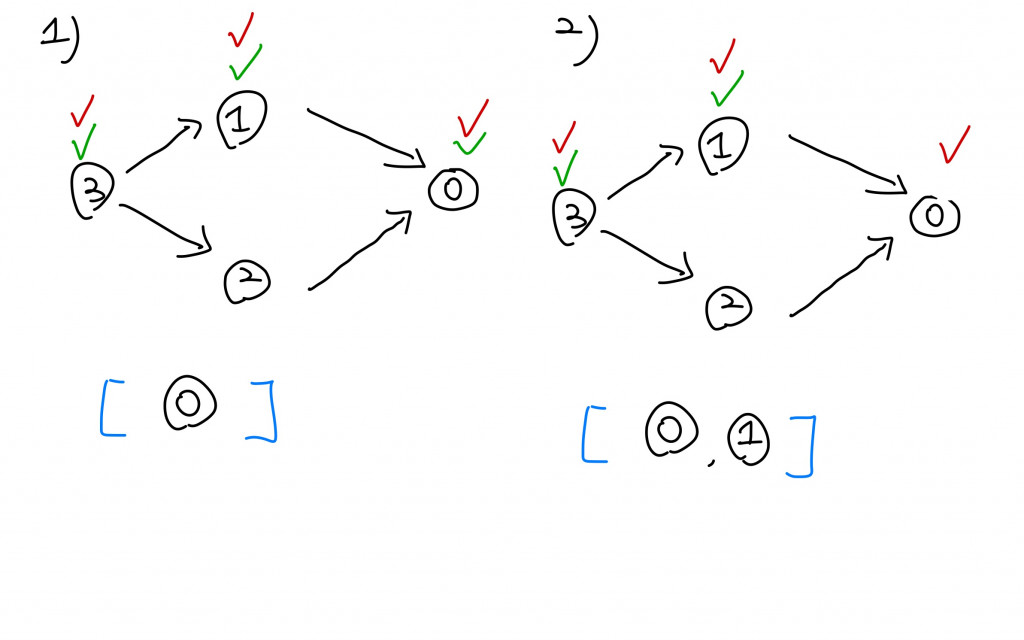

當節點已經沒有其他可以指向並且尚未拜訪過的節點時，就把他放入到list中，比如(2)中的1號課程因為已經拜訪過0號課程了，且沒有其他需要拜訪的節點所以就將他放入到list中。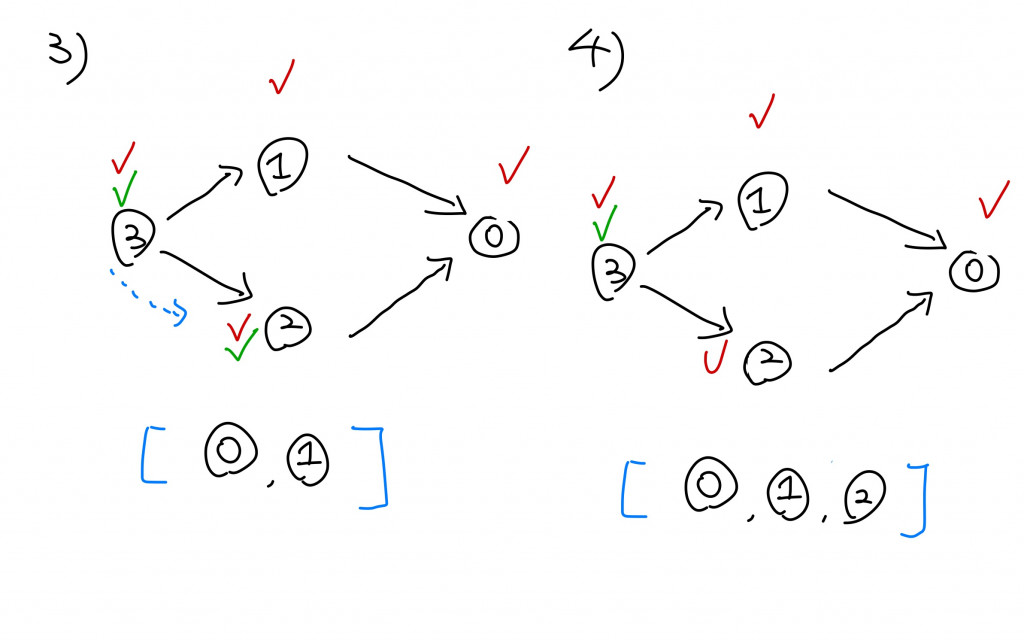

3號課程需要再去拜訪2號課程，所以在(3)時不會被放入到list中。
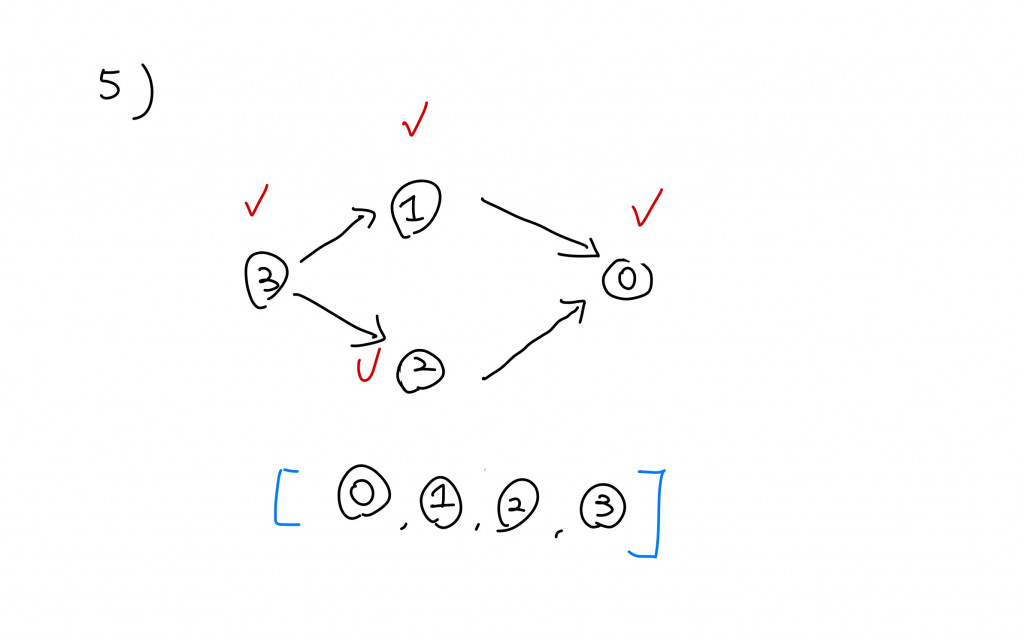
最後我們在(5)時得到正確的修課順序。

class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        adjList = defaultdict(list)
        for c1, c2 in prerequisites:
            adjList[c1].append(c2)
        
        visit = set()
        res = []

        def dfs(node, path):
            if node in path:
                return False
            if node in visit:
                return True
            
            visit.add(node)
            path.add(node)

            if node in adjList:
                for crs in adjList[node]:
                    if not dfs(crs, path):
                        return False
            
            res.append(node)
            path.remove(node)

            return True
        
        for crs in range(numCourses):
            if not dfs(crs, set()):
                return []
        return res

今天沒有達到自己預設的分享兩題，真的很懊悔，還要再繼續努力。