Hi 大家好，今天要先補齊昨天原本就要分享完的Topological sort的題目。
...原本是打算講解完題目後接著介紹Union-Find，但是這個題目的解析和程式碼都很長，所以就改成明天了👉👈
這題我花了一個多小時才解開😅 但是弄懂要怎麼解的瞬間真的覺得這題目很有趣，把解題想到的感覺也加到裡面和大家分享：）

Leetcode 2127. Maximum Employees to Be Invited to a Meeting

題目敘述：有一間公司，裡面有n位員工，每個員工都只有一個在這家公司裡喜歡的人（這件事很重要，要記著）。有一張圓桌，員工需要旁邊坐著自己喜歡的人才會來參加會議（超任性），請問總共最多可以邀請多少人來參加會議？
我們會得到一個input array叫favorite，來表示第i號員工喜歡的人是favortie[i]。

Example1:

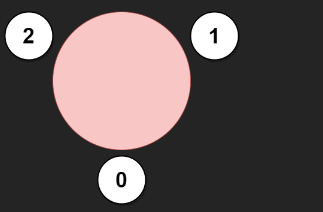
Input: favorite = [2,2,1,2]
Output: 3
Explanation: 以上圖示展示了公司如何邀請員工0、1和2，並讓他們在圓桌旁就座。
不能邀請所有員工，因為員工2不能同時坐在員工0、1和3的旁邊。
請注意，公司也可以邀請員工1、2和3，並讓他們坐在他們想要的位置。
參加會議的員工最大人數是3。

(圖源：leetcode)

Example2:

Input: favorite = [3,0,1,4,1]
Output: 4

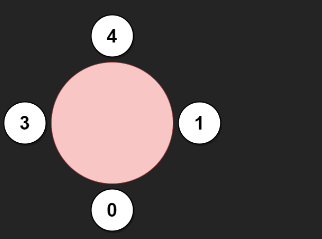
如果你看懂上面的題目敘述就來聽聽看我的分析吧。
首先，我們來討論看看根據每個人都只有一位喜歡的人這個規則下圖可能會長怎樣，我們假設a喜歡b的話會以a->b來表示：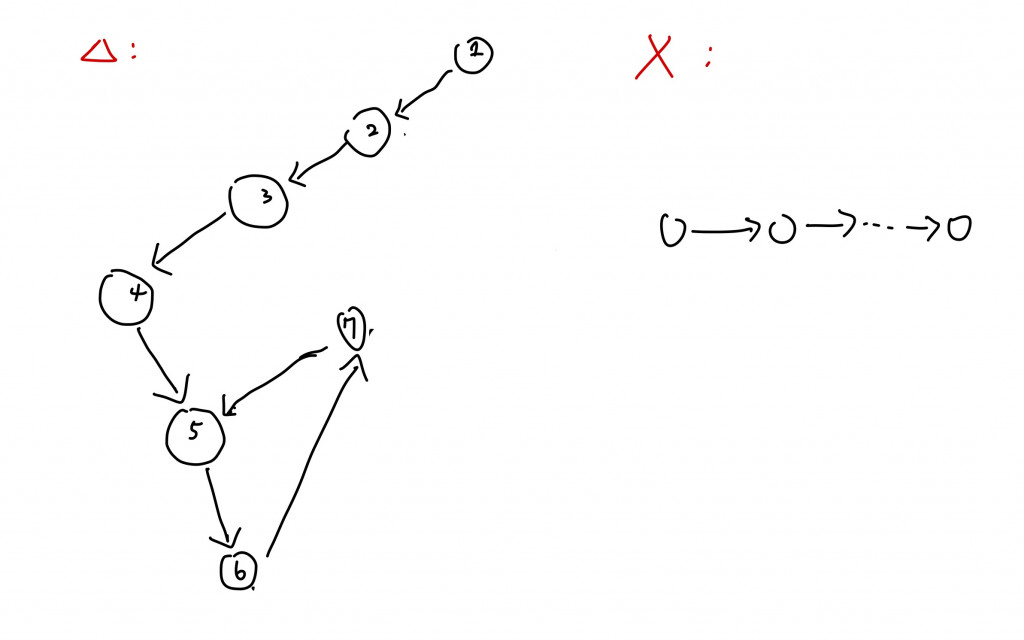

右邊打叉的圖（鏈結）不會存在的原因是因為最後面那一個節點沒有連向其他節點（一定要喜歡一個人）；而左邊打了三角形的圖是因為節點1~4號都是無法邀請的節點，我們只能邀請形成迴圈的5~7號節點。因為鏈結的最後一個一定要在指向某個節點，如圖就算指向了自己已形成回圈的某個節點也無法形成有效的答案，因為迴圈內的節點可以自行圍成一個圓圈就代表了一種合法的會議坐位坐法（但未必是最多人數的）。所以單相思的就不要再亂入到多角戀的劇情裡了（誤）

再來看圖可能會長怎樣：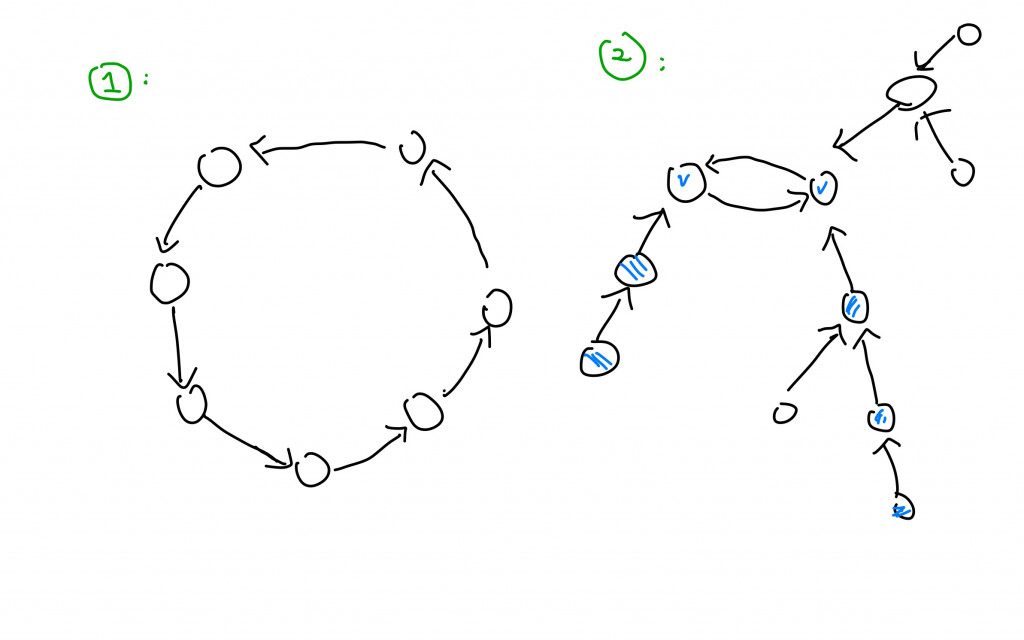

第一個情況剛才說過了這些節點剛好就自成一個圓形的坐法；第二種情況是出現了兩情相悅的組合啦，注意看兩情相悅的節點（藍勾勾），有藍勾勾的節點不會再指向別的節點了（ 因為我們工程師喜歡純愛，因為題目規定每個人只喜歡一人） ，雖然有可能會有別的節點指向他們。這時候我們要計算的是「指向藍勾勾節點中的最長路徑，總共會分別有兩條最長路徑加上這兩個兩情相悅的節點」。

還有一種情況有多個兩情相悅的組合加上迴圈：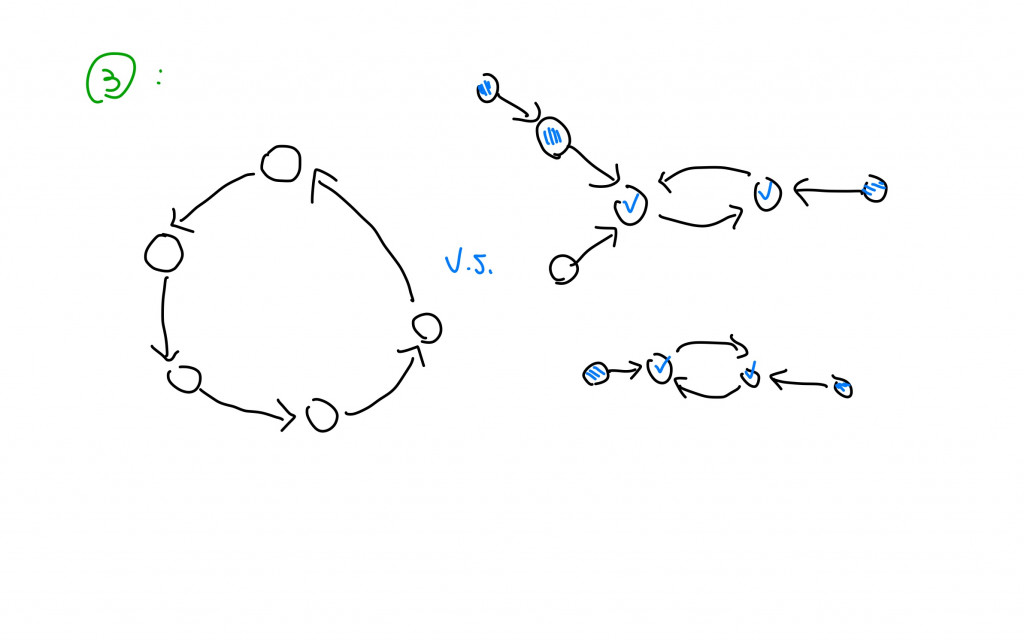

兩情相悅的組合：-> -> -> <- <- <- 有兩組，這種的可以都邀請到圓桌上，所以要把他們節點的總數計算出來和最大的迴圈比較。

我們分析完所有情況，現在要來考慮怎麼計算了，要算出：

1. 圖中最長的迴圈
2. 兩情相悅的節點以和指向他們的兩條最長路徑稱之為兩情相悅組合，一個Graph內可能有好幾個這種component，全部加總

我們遇到的問題是：

1. 前面打紅色三角形的圖的case:鏈結搭配迴圈，怎麼只計算出迴圈。
2. 兩情相悅組合要怎麼去找出指向藍勾勾節點的最長路徑

看到圖的節點拜訪又看到路徑，你應該會很想使用DFS(吧)，只是這樣看起來還是窒礙難行。這時候就要對DFS使用術式反轉 對用來表示喜歡的關係的箭頭進行反轉（稱之為某人對某人是必要的存在）來建Adjacency List。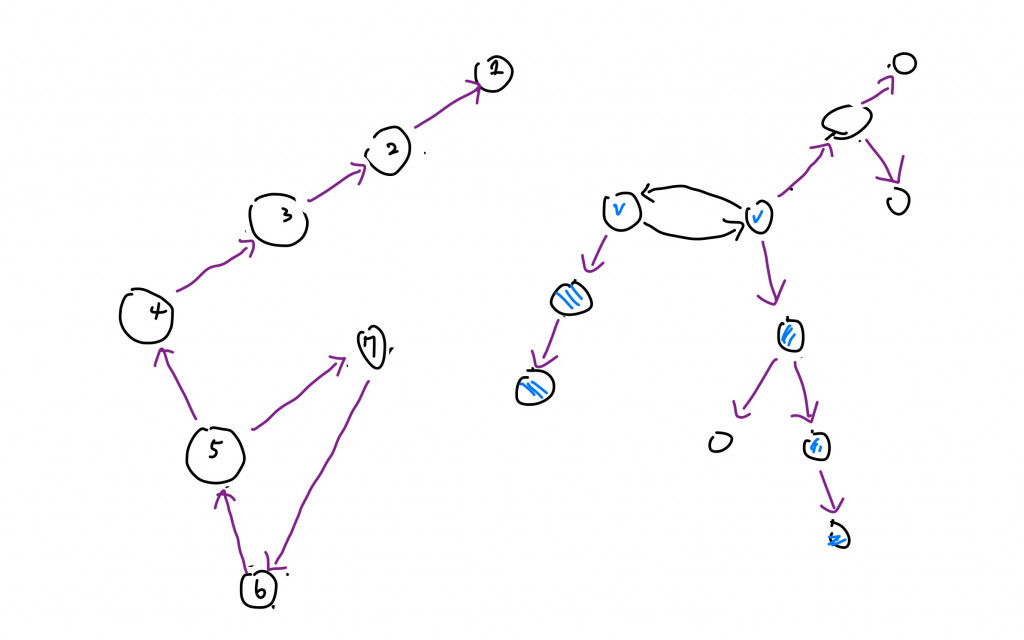

再使用post-order DFS。因為要算兩種類型的路徑，所以使用了兩種post-order DFS的函數去計算，最後再去比較他們的大小。

class Solution:
    def maximumInvitations(self, favorite: List[int]) -> int:
        adjList = defaultdict(list)
        pairs = []

        for i in range(len(favorite)):            
            if i in adjList and favorite[i] in adjList[i]:
                pairs.append([i, favorite[i]])
            adjList[favorite[i]].append(i)

        # print(pairs)
        
        visit = set()
        cycle = set()
        cycleLen = 0

        def findCycle(node):
            if node in cycle:
                return len(cycle)
            
            if node in visit:
                return 0
            
            cycle.add(node)
            res = 0
            if node in adjList:
                for n in adjList[node]:
                    res = max(res, findCycle(n))
            
            visit.add(node)
            cycle.remove(node)
            return res
        
        for n in range(len(favorite)):
            cycleLen = max(cycleLen, findCycle(n))
        

        def longestPath(node, path):
            if node not in adjList:
                return 1
            
            path.add(node)
            res = 0
            for n in adjList[node]:
                res = max(res, 1 + longestPath(n, path))
            
            path.remove(node)
            return res

        total = 0    
        for [n1, n2] in pairs:
            arm1, arm2 = 0, 0
            for n in adjList[n1]:
                if n != n2:
                    arm1 = max(arm1, longestPath(n, set()))
            
            for n in adjList[n2]:
                if n != n1:
                    arm2 = max(arm2, longestPath(n, set()))
                    
            
            total += arm1 + arm2 + 2

        # print(total)
        return max(total, cycleLen)
            

祝大家雙十連假愉快～