Hi 大家好，今天要繼續攻略和Graph有關的演算法，中文叫做拓璞排序。很常用來說明這個演算法的例子就是之前在介紹Adjacency List時分享其中一題leetcode：course schedule。
另外，這種演算法只能使用在沒有迴圈的有向圖上。我們直接看下面的示意圖。

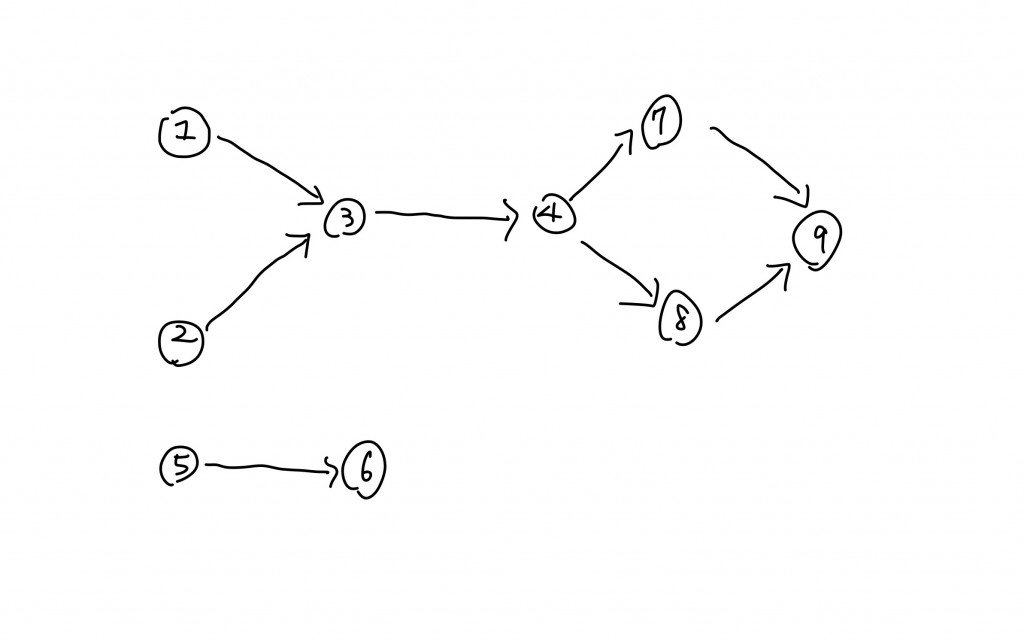
假設有九門課，有些課程需要先修別的課程才能修，我們以上圖表示，並且我們想利用程式碼輸出正確的修課順序。
我們可以對這張圖進行"Post-Order DFS"，也就是當某個節點可以指向的節點都已經被拜訪過了，才能將此節點放入到list中；或是該節點沒有可以其他可以拜訪的節點，我們以下圖表示。在下圖中我們可以看到紅色的數字代表拜訪該節點的順序。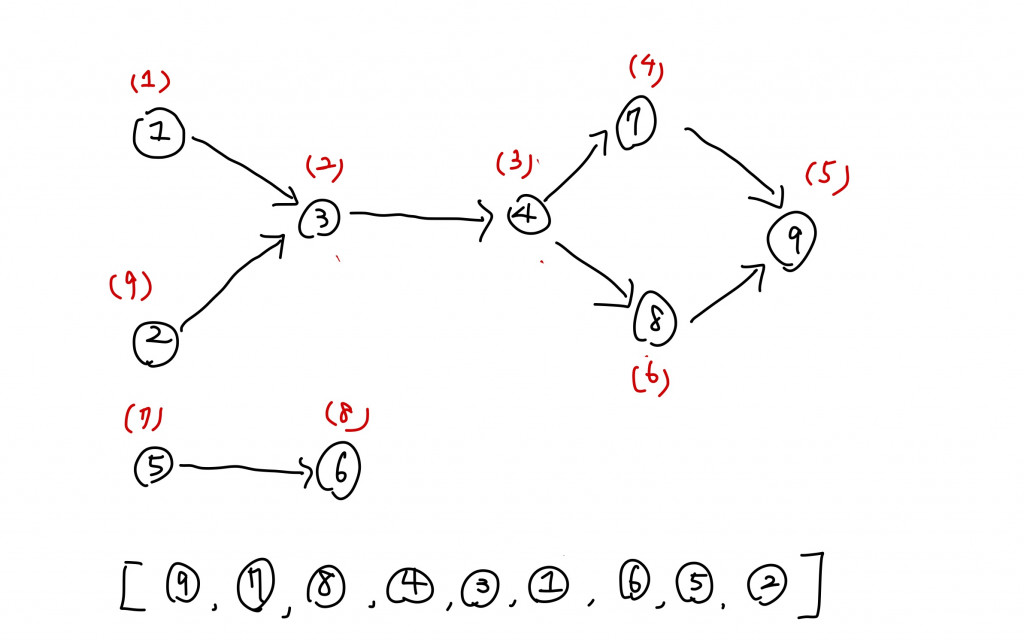

value為9的節點是通過DFS第五個被拜訪的節點，因為它已經沒有其他可以拜訪的節點所以會被放入到list中，並且遞迴結束，所以返回到value為7的節點，此節點除了指向value為9的節點沒有其他節點，並且他也被記錄為拜訪過了。所以把value為7的節點也放入到list中。返回遞迴到value為4的節點，此節點還有一個節點是尚未拜訪的，所以會DFS到value為8的節點，此節點的下一個節點已被拜訪(value:9)，所以把它加到list中，返回遞迴到value:4，這時候就可以把它放入到list中。依此類推到value:1的節點。

希望上一段各位看得懂我想表達的，接著我們看到第七個被拜訪的為value:5的節點也依同樣的原理來進行post-order dfs。最後我們得到以這種順序加入到list的各課程。

這順序看起來完全不對...你可能會想這麼說，但是當把這個list反轉後就大功告成。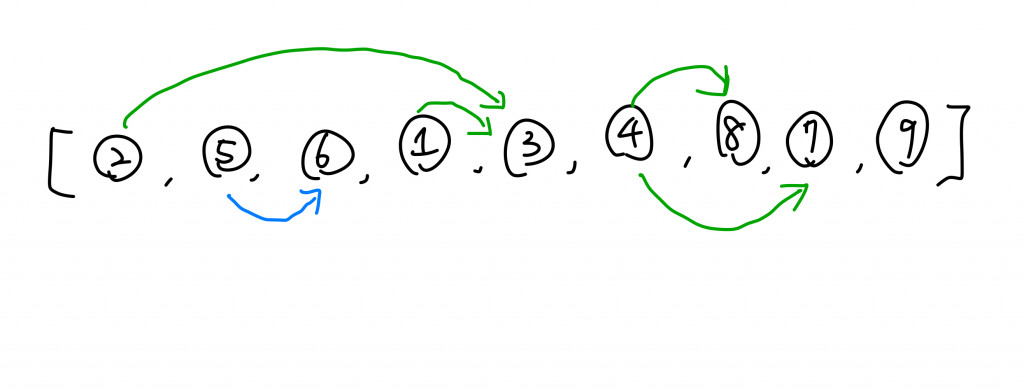

這是其中一種有效的答案（可能有多種有效的答案）。可以看到我們會先修完課程1、2才修課程3，雖然中間夾雜了先修課程5、6(而且5在6前面)也是沒有違反規則的。

說明了這麼多，現在來看程式碼吧。只要記得「先遞迴到最後，並且後面沒有東西或是已經拜訪過了再把節點放進list」就好。

# n代表課程1~n
# edges代表先修的條件，[[1,3],[2,3],...]

def topologicalSort(edges, n):
    adj = {}
    for i in range(1, n + 1):
        adj[i] = []
    for src, dst in edges:
        adj[src].append(dst)

    topSort = []
    visit = set()
    for i in range(1, n + 1):
        dfs(i, adj, visit, topSort)
    topSort.reverse()
    return topSort

def dfs(src, adj, visit, topSort):
    if src in visit:
        return
    visit.add(src)

    for neighbor in adj[src]:
        dfs(neighbor, adj, visit, topSort)
    topSort.append(src)

然後記得最後要反轉list呀

除了上面這種解法外，我們也可以直接將原本的圖的edge先進行反轉。這樣就可以直接進行一般的DFS，也不用再反轉list。但是這種修改圖的做法要根據之後是否還需要原圖來決定。當然如果題目一開始就給我們反轉的圖（例如上面提到的course schedule）那我們就蠻幸運的。

最一開始有提到這個演算法不能使用在有迴圈的圖上，所以當有可能有迴圈出現時，我們需要修改一下這個演算法去讓他能察覺有回圈並中止運行。題目的話明天會繼續，謝謝觀看。

Topological Sort就是DFS的術式反轉...啊抱歉太油了≖‿≖