分群理論

• 群內差異小，群間差異大
• 找出比較相似的資料聚集在一起，形成集群（Cluster）
• 相似性的依據是採用歐式距離，相對距離愈近、相似程度越高，被歸類至同一群組。
• 演算法：Kmeans, Hierarchical Clustering

k-means

from sklearn import cluster, datasets
# 讀入鳶尾花資料
iris = datasets.load_iris()
iris_X = iris.data
# KMeans 演算法
kmeans_fit = cluster.KMeans(n_clusters=3).fit(iris_X)

# 印出分群結果
cluster_labels = kmeans_fit.labels_
print("分群結果：")
print(cluster_labels)
print("---")

# 印出品種看看
iris_y = iris.target
print("真實品種：")
print(iris_y)

DBSCAN

一種密度基礎的空間分群方法，用於將資料點分成集群（cluster）和噪聲點（noise）

• 資料點（Data Points）
  資料集中的個體或觀測值，通常表示為N維空間中的點。

• 半徑（Radius，ε）
  DBSCAN使用半徑來定義每個資料點的鄰域範圍，資料點在這個範圍內視為鄰居。

• 核心點（Core Point）
  核心點是指在其半徑範圍內擁有至少MinPts個鄰居的資料點。

• 邊界點（Border Point）
  邊界點是指在其半徑範圍內鄰居數量不足MinPts的資料點，但可以連接到一個核心點而成為該集群的一部分。

• 噪聲點（Noise Point）
  噪聲點是指在半徑範圍內無核心點鄰居的資料點，它們被視為孤立的資料點或雜訊。

• ε-鄰域（ε-Neighborhood）
  ε-鄰域表示以某個資料點為中心，半徑為ε的區域，包含在這個區域內的所有資料點被視為鄰居。

• 核心物件集合（Core Object Set）
  核心物件集合包含所有核心點及其相關的連接邊界點。

• 邊界物件集合（Border Object Set）
  邊界物件集合包含所有邊界點，這些點是與核心點相關聯的資料點。

import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
import numpy as np

data = np.array([[1, 2], [5, 8], [1.5, 1.8], [8, 8], [1, 0.6], [9, 11]])

# 初始化DBSCAN模型，指定eps（半徑）和min_samples（最小樣本數）
dbscan = DBSCAN(eps=2, min_samples=2)

# 適配模型到數據
dbscan.fit(data)

# 獲取每個數據點的分群標籤，-1 表示噪聲點
labels = dbscan.labels_

print("分群標籤:", labels)

# 取得 DBSCAN 的分群結果
core_samples_mask = np.zeros_like(labels, dtype=bool)
core_samples_mask[dbscan.core_sample_indices_] = True

# 繪製分群結果
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
          for each in np.linspace(0, 1, len(unique_labels))]

for k, col in zip(unique_labels, colors):
    if k == -1:
        # 噪聲點以黑色表示
        col = [0, 0, 0, 1]

    class_member_mask = (labels == k)

    xy = data[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=14, label=f'Cluster {k}')

    xy = data[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=6)

plt.title('DBSCAN Clustering Result')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc='best')
plt.show()

譜分群(Spectral Clustering)

譜分群是一種基於資料的特徵間的相似性矩陣進行分群的方法，通常用於圖分割和文本分類等應用。

• 步驟：

1. 創建相似性矩陣。
   NxN矩陣，其中N是資料點的數量。相似性矩陣用於表示每對資料點之間的相似性或距離。通常使用歐氏距離、餘弦相似度等來計算相似性
2. 將相似性矩陣轉換為拉普拉斯矩陣。
3. 求解拉普拉斯矩陣的特徵向量。
4. 使用K均值等算法對特徵向量進行分群。

import numpy as np
from sklearn.cluster import SpectralClustering
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

data, ground_truth = make_blobs(
    n_samples=300, centers=3, cluster_std=1.0, random_state=42)

# 初始化譜分群模型，指定集群數和相似性矩陣的配置
n_clusters = 3
spectral_clustering = SpectralClustering(
    n_clusters=n_clusters, affinity='nearest_neighbors')

# 適配模型到數據
labels = spectral_clustering.fit_predict(data)

# 繪製分群結果
plt.scatter(data[:, 0], data[:, 1], c=labels, cmap='viridis')
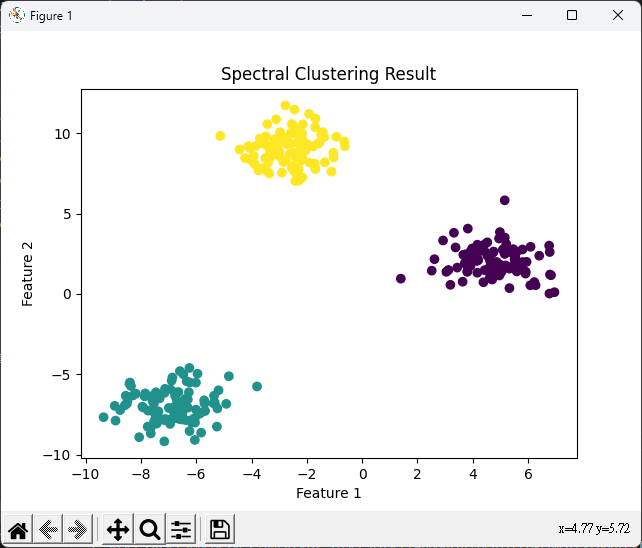
plt.title('Spectral Clustering Result')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

地真(ground truth)

• 真實的或事實的資料分群結果，通常用於評估分群算法的性能。
• 監督式學習訓練集合的分類準確度

同質性

• 測量了每個分群只包含一個類別的程度。
• 同質性越高，表示每個集群都包含相同類別的資料

完整性

• 測量了每個類別是否都被分配到了同一分群中。
• 完整性越高，表示每個類別都完全包含在一個集群中

蘭德指數(adjusted rand index,ARI)

• 介於-1和1之間的指數，衡量分群結果與地真之間的一致性。
• ARI越接近1，表示分群結果越接近地真。

from sklearn.metrics import homogeneity_score, completeness_score, adjusted_rand_score
import numpy as np

# 真實分群結果
true_labels = np.array([0, 0, 1, 1, 2, 2])

# 假設的分群結果
predicted_labels = np.array([0, 0, 2, 2, 1, 1])

# 計算同質性
homogeneity = homogeneity_score(true_labels, predicted_labels)

# 計算完整性
completeness = completeness_score(true_labels, predicted_labels)

# 計算ARI
ari = adjusted_rand_score(true_labels, predicted_labels)

print("同質性：", homogeneity)
print("完整性：", completeness)
print("ARI：", ari)

階層式分群

• 將資料分為不同階層或層次的分群方法。它可以生成一個樹狀結構
• 通常用於層次性分析和可視化資料

from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
import numpy as np

data = np.random.rand(10, 2)

# 計算聚合連結矩陣
linkage_matrix = linkage(data, method='ward')

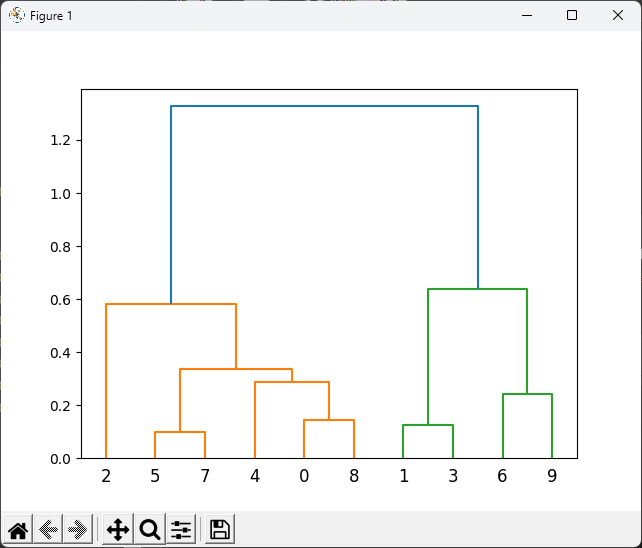
# 繪製樹狀圖
dendrogram(linkage_matrix)
plt.show()

聚合式分群(Agglomerative clustering)

相似性(Affinity)

階層式分群中的相似性通常使用距離度量。

• 歐氏距離(dE - Euclid) 或稱L2距離
  

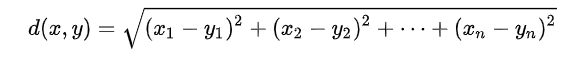
from scipy.spatial.distance import euclidean
point1 = [1, 2]
point2 = [4, 6]
distance = euclidean(point1, point2)
print("歐氏距離:", distance)

• 曼哈頓(dM - Manhattan)
  

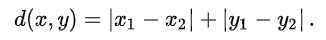
from scipy.spatial.distance import cityblock
point1 = [1, 2]
point2 = [4, 6]
distance = cityblock(point1, point2)
print("曼哈頓距離:", distance)

• 餘弦距離(Cosine)- 餘弦相似性

from sklearn.metrics.pairwise import cosine_similarity
import numpy as np
vector1 = np.array([1, 2, 3])
vector2 = np.array([4, 5, 6])
similarity = cosine_similarity([vector1], [vector2])
print("餘弦相似度:", similarity[0][0])

連結(linkage)

計算兩個集群之間的相似度。

• 完整連結(Complete linkage)

from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
data = np.array([[1, 2], [2, 3], [4, 5], [5, 6]])
# 使用完整連結進行階層分群
linkage_matrix = linkage(data, method='complete')
# 繪製階層分群樹
dendrogram(linkage_matrix)
plt.show()

• 平均連結(Average linkage)

from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
data = np.array([[1, 2], [2, 3], [4, 5], [5, 6]])
# 使用平均連結進行階層分群
linkage_matrix = linkage(data, method='average')
# 繪製階層分群樹
dendrogram(linkage_matrix)
plt.show()

• 沃德連結(Ward’s linkage)

from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
data = np.array([[1, 2], [2, 3], [4, 5], [5, 6]])
# 使用沃德連結進行階層分群
linkage_matrix = linkage(data, method='ward')
# 繪製階層分群樹
dendrogram(linkage_matrix)
plt.show()

分裂式分群(Divisive clustering)

• 一個含所有樣本的群聚，分群會拆分中間(intermediate)群聚，直到所有elements被分隔。
• 自頂向下的分群方法，它將所有資料點劃分為一個大集群，然後分割中間集群，直到所有資料點都被分割成單個集群。
• DIANA（Divisive Analysis）是一個常見的分裂式分群演算法，它將資料點分割為子集群。

from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt

data, ground_truth = make_blobs(
    n_samples=300, centers=4, cluster_std=1.0, random_state=42)

# 初始化階層式分群模型，並指定要分成的子集群數
n_clusters = 4
diana = AgglomerativeClustering(
    n_clusters=n_clusters, affinity='euclidean', linkage='ward')

# 適配模型到數據
diana.fit(data)

# 獲取每個數據點的分群標籤
labels = diana.labels_

# 繪製數據和分群結果
plt.scatter(data[:, 0], data[:, 1], c=labels, cmap='viridis')
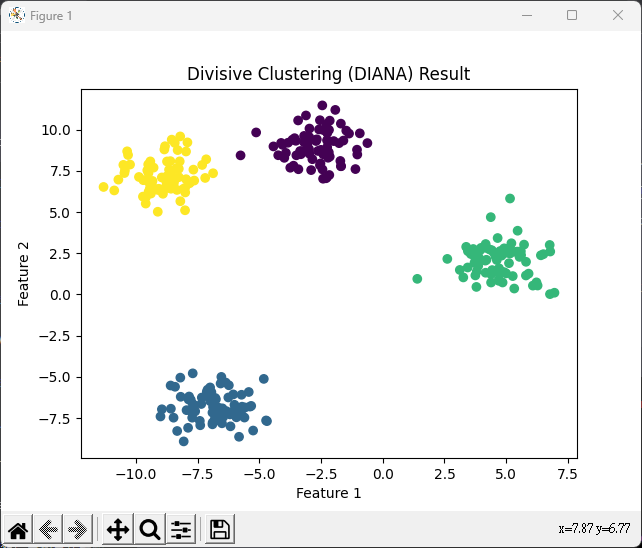
plt.title('Divisive Clustering (DIANA) Result')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()