非監督式學習(分群-距離、相似特徵、歸納法)

分群演算法：

• K-Means 聚類：將數據分為 K 個不同的群集，每個群集由其內部的數據點的相似性來定義。

• 層次聚類(Hierarchical)：通過計算數據點之間的距離或相似性來建立層次結構，可以形成樹狀的聚類結構。

• DBSCAN 聚類：基於密度的聚類方法，根據數據點周圍的密度來擴展聚類。

• GMM 聚類：基於高斯分佈的混合模型，將數據點分為多個高斯分佈組成的群集。

肘部法則圖 (Elbow Method)

1. KMeans
2. 計算不同 K 值下的 Inertia（內聚性），衡量了每個資料點到它所屬的中心點的距離的總和，
   通過遍歷不同的 K 值（通常從 1 開始到一個適當的上限，例如 10）
3. 繪製肘部法則圖，X 軸代表 K 值，Y 軸代表 Inertia。隨著 K 值的增加，Inertia 會逐漸減小，因為每個群的內部成員距離中心更近。但是，當 K 值增加到一個合適的程度時，Inertia 的下降速度會減緩，形成一個「肘部」。
4. 選擇最佳 K 值：肘部法則建議選擇肘部所在的 K 值，因為這表示在這個點後，增加 K 值不再顯著提高模型性能。

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成一個虛擬資料集
data, _ = make_blobs(n_samples=300, centers=4, random_state=0, cluster_std=1.0)

# 初始化存儲不同 K 值下 Inertia 的列表
inertia_values = []

# 設定 K 值範圍
k_values = range(1, 11)

# 計算不同 K 值下的 Inertia
for k in k_values:
    kmeans = KMeans(n_clusters=k, random_state=0)
    kmeans.fit(data)
    inertia_values.append(kmeans.inertia_)

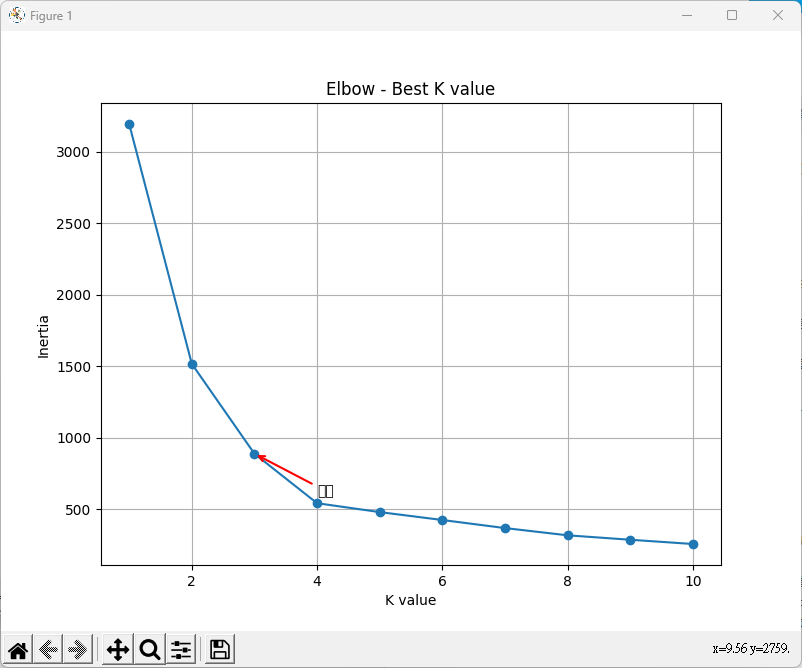
# 繪製肘部法則圖
plt.figure(figsize=(8, 6))
plt.plot(k_values, inertia_values, marker='o', linestyle='-')
plt.xlabel('K value')
plt.ylabel('Inertia')
plt.title('Elbow - Best K value')
plt.grid(True)

# 添加肘部位置的標註
plt.annotate('肘部', xy=(3, inertia_values[2]), xytext=(4, 600),
             arrowprops=dict(arrowstyle='->', lw=1.5, color='red'))
plt.show()

K-means

• 可巨量資料分群
• k個質心跟均數
• 相關重要內容:
  • 將惰性最佳化
  • 輪廓分數
  • Calinski-Harabasz 指數
  • 群聚不穩度

Iris Database - K-means

• Python

from sklearn import cluster, datasets

# 讀入鳶尾花資料
iris = datasets.load_iris()
iris_X = iris.data

# KMeans 演算法
kmeans_fit = cluster.KMeans(n_clusters=3).fit(iris_X)

# 印出分群結果
cluster_labels = kmeans_fit.labels_
print("分群結果：")
print(cluster_labels)
print("---")

# 印出品種看看
iris_y = iris.target
print("真實品種：")
print(iris_y)

分群結果：
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 2 2 2 0 2 2 2 2
 2 2 0 0 2 2 2 2 0 2 0 2 0 2 2 0 0 2 2 2 2 2 0 2 2 2 2 0 2 2 2 0 2 2 2 0 2
 2 0]
---
真實品種：
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

• R

# 讀入鳶尾花資料
iris_kmeans <- iris[, -5]

# KMeans 演算法
kmeans_fit <- kmeans(iris_kmeans, nstart=20, centers=3)

# 印出分群結果
kmeans_fit$cluster

# 印出品種看看
iris$Species

> iris$Species
  [1] setosa     setosa     setosa     setosa     setosa     setosa    
  [7] setosa     setosa     setosa     setosa     setosa     setosa    
 [13] setosa     setosa     setosa     setosa     setosa     setosa    
 [19] setosa     setosa     setosa     setosa     setosa     setosa    
 [25] setosa     setosa     setosa     setosa     setosa     setosa    
 [31] setosa     setosa     setosa     setosa     setosa     setosa    
 [37] setosa     setosa     setosa     setosa     setosa     setosa    
 [43] setosa     setosa     setosa     setosa     setosa     setosa    
 [49] setosa     setosa     versicolor versicolor versicolor versicolor
 [55] versicolor versicolor versicolor versicolor versicolor versicolor
 [61] versicolor versicolor versicolor versicolor versicolor versicolor
 [67] versicolor versicolor versicolor versicolor versicolor versicolor
 [73] versicolor versicolor versicolor versicolor versicolor versicolor
 [79] versicolor versicolor versicolor versicolor versicolor versicolor
 [85] versicolor versicolor versicolor versicolor versicolor versicolor
 [91] versicolor versicolor versicolor versicolor versicolor versicolor
 [97] versicolor versicolor versicolor versicolor virginica  virginica 
[103] virginica  virginica  virginica  virginica  virginica  virginica 
[109] virginica  virginica  virginica  virginica  virginica  virginica 
[115] virginica  virginica  virginica  virginica  virginica  virginica 
[121] virginica  virginica  virginica  virginica  virginica  virginica 
[127] virginica  virginica  virginica  virginica  virginica  virginica 
[133] virginica  virginica  virginica  virginica  virginica  virginica 
[139] virginica  virginica  virginica  virginica  virginica  virginica 
[145] virginica  virginica  virginica  virginica  virginica  virginica 
Levels: setosa versicolor virginica

性能評估 - K-means

• 數值愈接近 1 表示愈好，反之愈接近 -1 表示愈差。
• Python

from sklearn import cluster, datasets, metrics

# 讀入鳶尾花資料
iris = datasets.load_iris()
iris_X = iris.data

# KMeans 演算法
kmeans_fit = cluster.KMeans(n_clusters=3).fit(iris_X)
cluster_labels = kmeans_fit.labels_

# 印出績效
silhouette_avg = metrics.silhouette_score(iris_X, cluster_labels)
print(silhouette_avg)

0.5528190123564095

如何選擇 k

• 隨著 k 值的增加，K-Means 演算法的績效一定會愈來愈好，當 k = 觀測值數目的時候，我們會得到一個組間差異最大，組內差異最小的結果。

• Python

from sklearn import cluster, datasets, metrics
import matplotlib.pyplot as plt

# 讀入鳶尾花資料
iris = datasets.load_iris()
iris_X = iris.data

# 迴圈
silhouette_avgs = []
ks = range(2, 11)
for k in ks:
    kmeans_fit = cluster.KMeans(n_clusters=k).fit(iris_X)
    cluster_labels = kmeans_fit.labels_
    silhouette_avg = metrics.silhouette_score(iris_X, cluster_labels)
    silhouette_avgs.append(silhouette_avg)

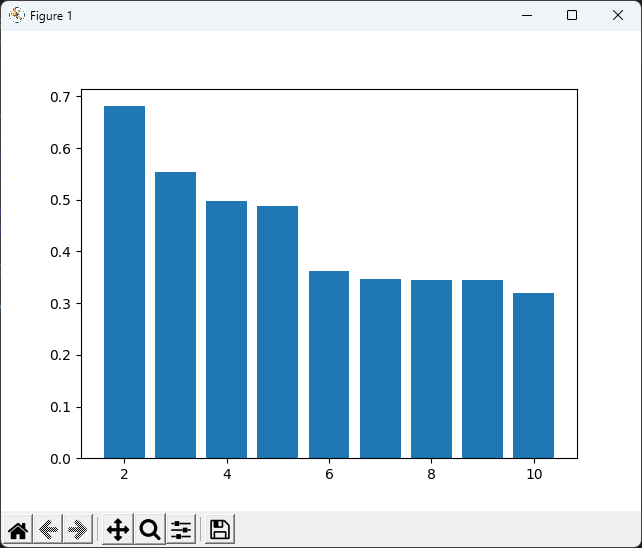
# 作圖並印出 k = 2 到 10 的績效
plt.bar(ks, silhouette_avgs)
plt.show()
print(silhouette_avgs)

• k 值在等於 2 與 3 的時候 K-Means 演算法的績效較好，這也驗證了我們先前的觀察，setosa 這個品種跟另外兩個品種在花瓣（Petal）的長和寬跟花萼（Sepal）的長和寬有比較大的差異，因此如果是以 K-Means 分群，可能會將 setosa 歸為一群，versicolor 和 virginica 歸為一群。
  

層次聚類 ( Hierarchical )

• 不可巨量資料分群
• 分為聚合型、分裂型

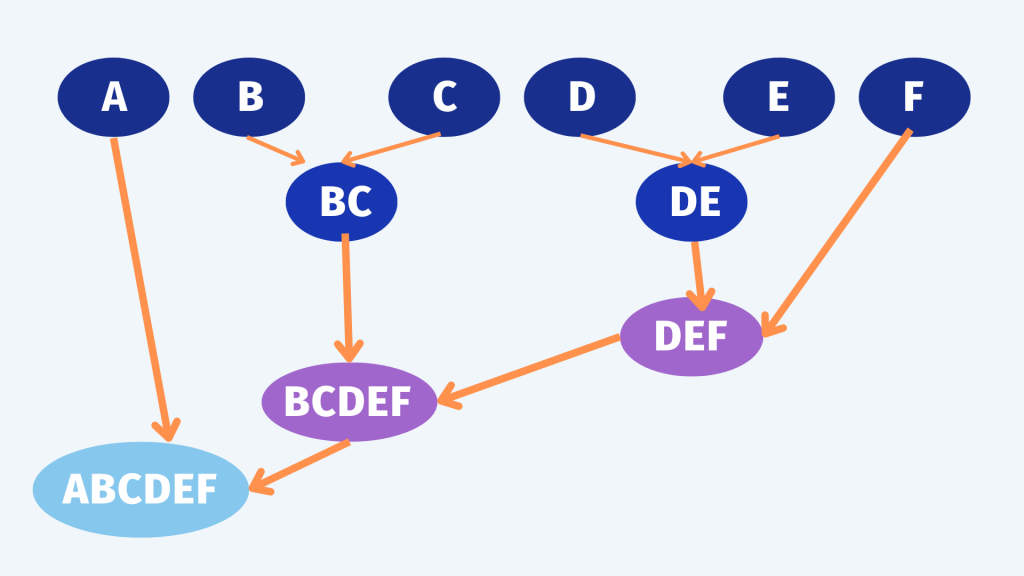
把每一個點當作一個群組
透過掃描過整個資料及尋找出最近的兩個群組，並把這兩個點榜再一起變成一個群組
尋找下一個最近的的兩個群組，再綁再一起變成一個群組
停止: 直到所有資料都被分成一群，或是透過設定參數到分到幾個群時自動停止

Iris Database - Hierarchical Clustering

• Python

from sklearn import cluster, datasets

# 讀入鳶尾花資料
iris = datasets.load_iris()
iris_X = iris.data

# Hierarchical Clustering 演算法
hclust = cluster.AgglomerativeClustering(
    linkage='ward', affinity='euclidean', n_clusters=3)

# 印出分群結果
hclust.fit(iris_X)
cluster_labels = hclust.labels_
print(cluster_labels)
print("---")

# 印出品種看看
iris_y = iris.target
print(iris_y)

[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 2 2 2 0 2 2 2 2
 2 2 0 0 2 2 2 2 0 2 0 2 0 2 2 0 0 2 2 2 2 2 0 0 2 2 2 0 2 2 2 0 2 2 2 0 2
 2 0]
---
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

• 看起來 setosa 這個品種跟另外兩個品種在花瓣（Petal）的長和寬跟花萼（Sepal）的長和寬有比較大的差異。

• R

# 讀入鳶尾花資料
iris_hclust <- iris[, -5]

# Hierarchical Clustering 演算法
dist_matrix <- dist(iris_hclust)
hclust_fit <- hclust(dist_matrix, method = "single")
hclust_fit_cut <- cutree(hclust_fit, k = 3)

# 印出分群結果
hclust_fit_cut

# 印出品種看看
iris$Species

> 
> # 印出分群結果
> hclust_fit_cut
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [73] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[109] 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2
[145] 2 2 2 2 2 2
> 
> # 印出品種看看
> iris$Species
  [1] setosa     setosa     setosa     setosa     setosa     setosa    
  [7] setosa     setosa     setosa     setosa     setosa     setosa    
 [13] setosa     setosa     setosa     setosa     setosa     setosa    
 [19] setosa     setosa     setosa     setosa     setosa     setosa    
 [25] setosa     setosa     setosa     setosa     setosa     setosa    
 [31] setosa     setosa     setosa     setosa     setosa     setosa    
 [37] setosa     setosa     setosa     setosa     setosa     setosa    
 [43] setosa     setosa     setosa     setosa     setosa     setosa    
 [49] setosa     setosa     versicolor versicolor versicolor versicolor
 [55] versicolor versicolor versicolor versicolor versicolor versicolor
 [61] versicolor versicolor versicolor versicolor versicolor versicolor
 [67] versicolor versicolor versicolor versicolor versicolor versicolor
 [73] versicolor versicolor versicolor versicolor versicolor versicolor
 [79] versicolor versicolor versicolor versicolor versicolor versicolor
 [85] versicolor versicolor versicolor versicolor versicolor versicolor
 [91] versicolor versicolor versicolor versicolor versicolor versicolor
 [97] versicolor versicolor versicolor versicolor virginica  virginica 
[103] virginica  virginica  virginica  virginica  virginica  virginica 
[109] virginica  virginica  virginica  virginica  virginica  virginica 
[115] virginica  virginica  virginica  virginica  virginica  virginica 
[121] virginica  virginica  virginica  virginica  virginica  virginica 
[127] virginica  virginica  virginica  virginica  virginica  virginica 
[133] virginica  virginica  virginica  virginica  virginica  virginica 
[139] virginica  virginica  virginica  virginica  virginica  virginica 
[145] virginica  virginica  virginica  virginica  virginica  virginica 
Levels: setosa versicolor virginica
> 

性能評估 - Hierarchical Clustering

• Python

from sklearn import cluster, datasets, metrics

# 讀入鳶尾花資料
iris = datasets.load_iris()
iris_X = iris.data

# Hierarchical Clustering 演算法
hclust = cluster.AgglomerativeClustering(
    linkage='ward', affinity='euclidean', n_clusters=3)

# 印出績效
hclust.fit(iris_X)
cluster_labels = hclust.labels_
silhouette_avg = metrics.silhouette_score(iris_X, cluster_labels)
print(silhouette_avg)

0.5543236611296419

• R

library(GMD)

# 讀入鳶尾花資料
iris_hclust <- iris[, -5]

# Hierarchical Clustering 演算法
dist_matrix <- dist(iris_hclust)
hclust_fit <- hclust(dist_matrix)
hclust_fit_cut <- cutree(hclust_fit, k = 3)

# 印出績效
hc_stats <- css(dist_matrix, clusters = hclust_fit_cut)
hc_stats$totwss / hc_stats$totbss

# Dendrogram
plot(hclust_fit)
rect.hclust(hclust_fit, k = 2, border = "red")
rect.hclust(hclust_fit, k = 3, border = "green")

• 從 Dendrogram 看起來 setosa 這個品種跟兩個品種有比較大的差異，在 k = 2 或 k = 3 時都會被演算法歸類為獨立一群。

都來一遍

from sklearn.mixture import GaussianMixture
from sklearn.cluster import DBSCAN
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import metrics
from sklearn import cluster, datasets
import warnings

# Suppress FutureWarnings
warnings.simplefilter(action='ignore', category=FutureWarning)

# 讀入鳶尾花資料
iris = datasets.load_iris()
iris_X = iris.data

# KMeans 演算法
kmeans_fit = cluster.KMeans(n_clusters=3, n_init=10).fit(iris_X)


# 印出分群結果
cluster_labels = kmeans_fit.labels_
print("分群結果：")
print(cluster_labels)
print("---")

# 印出品種看看
iris_y = iris.target
print("真實品種：")
print(iris_y)
# ------------------------------------------------------------
# silhouette_avg
silhouette_avg = metrics.silhouette_score(iris_X, cluster_labels)
print("silhouette_avg: ", silhouette_avg)
# ------------------------------------------------------------
# calinski_harabasz_score
calinski_harabasz_score = metrics.calinski_harabasz_score(
    iris_X, cluster_labels)
print("calinski_harabasz_score: ", calinski_harabasz_score)
# ------------------------------------------------------------
# 群聚不穩度

# 計算不同 K 值的 KMeans 模型並記錄 inertia
inertia = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, random_state=0).fit(iris_X)
    inertia.append(kmeans.inertia_)

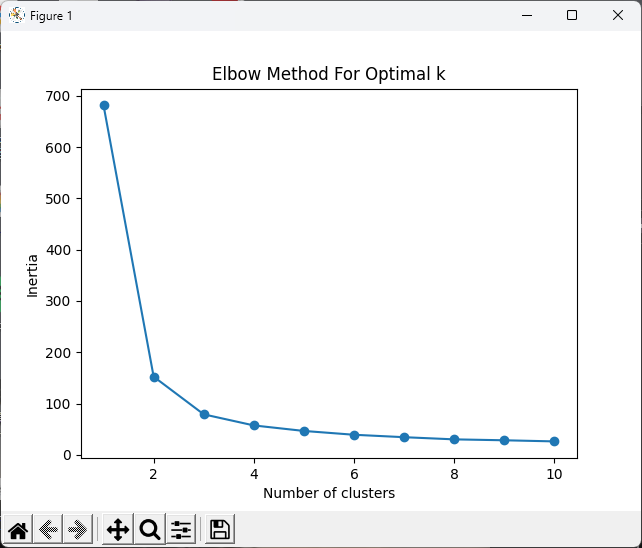
# 繪製肘部法則圖
plt.plot(range(1, 11), inertia, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('Elbow Method For Optimal k')
plt.show()
# ------------------------------------------------------------
# 層次聚類(Hierarchical)

# 設定分群數
n_clusters = 3

# 層次聚類模型
agg_clustering = AgglomerativeClustering(n_clusters=n_clusters)
agg_clustering.fit(iris_X)

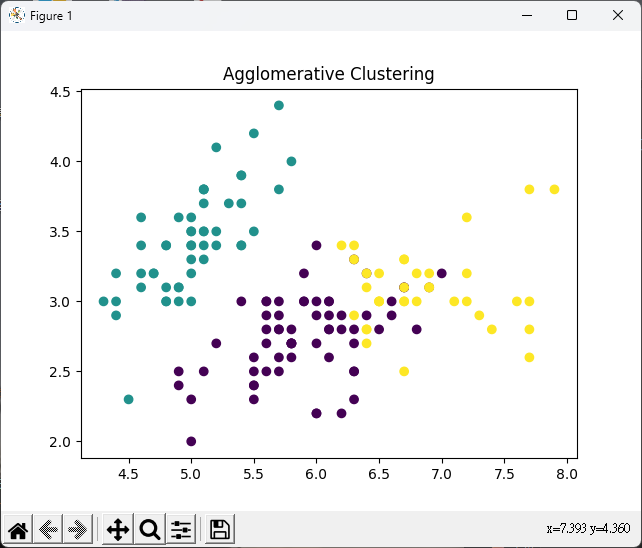
# 繪製散佈圖
plt.scatter(iris_X[:, 0], iris_X[:, 1], c=agg_clustering.labels_)
plt.title("Agglomerative Clustering")
plt.show()

# ------------------------------------------------------------
# DBSCAN

# DBSCAN 模型
dbscan = DBSCAN(eps=0.3, min_samples=5)
dbscan.fit(iris_X)

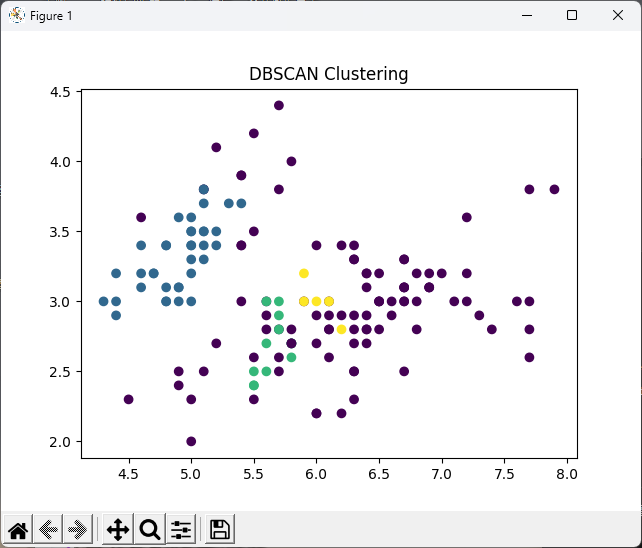
# 繪製散佈圖
plt.scatter(iris_X[:, 0], iris_X[:, 1], c=dbscan.labels_)
plt.title("DBSCAN Clustering")
plt.show()
# ------------------------------------------------------------
# GMM

# GMM 模型
gmm = GaussianMixture(n_components=3, random_state=0)
gmm.fit(iris_X)

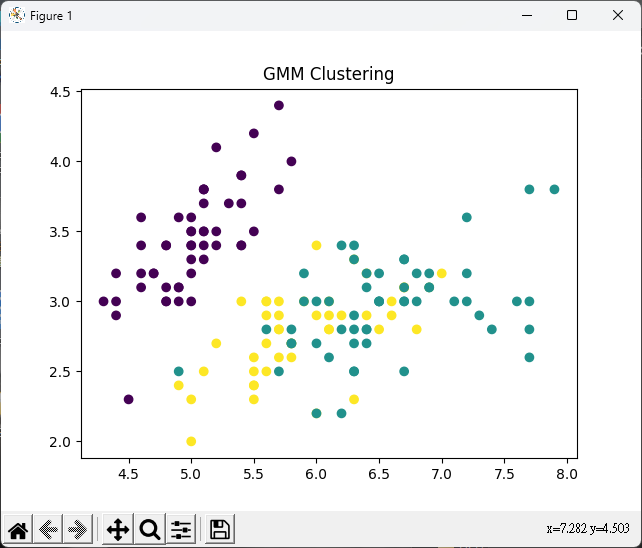
# 繪製散佈圖
plt.scatter(iris_X[:, 0], iris_X[:, 1], c=gmm.predict(iris_X))
plt.title("GMM Clustering")
plt.show()

分群結果：
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 2 2 2 1 2 2 2 2
 2 2 1 1 2 2 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 2 1 2 2 2 2 1 2 2 2 1 2 2 2 1 2
 2 1]
---
真實品種：
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
silhouette_avg:  0.5528190123564095
calinski_harabasz_score:  561.62775662962