105. Construct Binary Tree from Preorder and Inorder Traversal

解題程式碼

var buildTree = function (preorder, inorder) {
  if (!preorder.length || !inorder.length) return null;

  const root = new TreeNode(preorder[0]);
  const mid = inorder.indexOf(preorder[0]);
  root.left = buildTree(preorder.slice(1, mid + 1), inorder.slice(0, mid));
  root.right = buildTree(preorder.slice(mid + 1), inorder.slice(mid + 1));

  return root;
};

解題思路、演算法

這題題目要求從前序走訪、中序走訪後的結果，去組建出原本的二元樹，所以需要依照它們排序的特性去想辦法找出原本的二元樹。

以下分析幾點:

1. 前序走訪的第一個節點一定是整個樹的根節點，再來是左子樹一層層走訪的節點，最後是右子樹一層層走訪的節點，只是右子樹開始的節點無法從走訪結果得知。
2. 所以需要中序走訪的特性，已透過前序走訪求得整個樹的根節點，那在中序走訪中的陣列找到根節點位置後，其後面的節點就是右子樹的節點。
3. 這樣就知道前序走訪的結果中，右子樹是從哪個節點開始。在前序走訪、中序走訪後的結果陣列都知道根節點左右子樹在陣列中的範圍後，就可以取出做遞迴。

ex: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

1. 3 一定是整個樹的根節點。
2. 從 inorder 得知根節點 3 index = 1，把它記錄在 mid 變數，而 3 之前的一定是根節點的左子樹上的節點(9)，反之 3 之後的一定是根節點的右子樹上的節點(15,20,7)。
3. preorder 陣列內，左子樹取出 index 1~(mid + 1) 的範圍，此範圍為根節點的左子樹。inorder 取出 index 0~mid 的範圍，此範圍為根節點的左子樹。然後將切分出來的 preorder 子陣列和 inorder 做子陣列遞迴。
4. preorder 陣列內，右子樹取出 index mid + 1 之後的範圍，此範圍為根節點的右子樹。inorder 取出 mid + 1 之後的範圍，此範圍為根節點的右子樹。然後將切分出來的 preorder 子陣列和 inorder 做子陣列遞迴。

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(n)

參考資料

Construct Binary Tree from Inorder and Preorder Traversal - Leetcode 105 - Python

105. 从前序与中序遍历序列构造二叉树 Construct Binary Tree from Preorder and Inorder Traversal【LeetCode 力扣】

113. Path Sum II

解題程式碼

var pathSum = function (root, targetSum) {
  const result = [];

  const DFS = (node, path, sum) => {
    if (!node) return;

    path.push(node.val);
    sum += node.val;

    if (!node.left && !node.right && sum === targetSum) {
      result.push(path);
      return;
    }

    if (node.left) DFS(node.left, [...path], sum);
    if (node.right) DFS(node.right, [...path], sum);
  };
  DFS(root, [], 0);

  return result;
};

解題思路、演算法

這題使用 DFS 解題。

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(n)，n 為 tree height

參考資料

662. Maximum Width of Binary Tree

解題程式碼

var widthOfBinaryTree = function (root) {
  const DFS = (node, level, pos) => {
    if (!node) return;
    if (minPos[level] === undefined) minPos.push(pos); // 找到同層的最左節點編號

    const diff = pos - minPos[level];
    maxWidth = Math.max(maxWidth, diff + 1);

    DFS(node.left, level + 1, diff * 2);
    DFS(node.right, level + 1, diff * 2 + 1);
  };

  let maxWidth = 0;
  const minPos = [0];
  DFS(root, 0, 0);

  return maxWidth;
};

解題思路、演算法

我們可以把題目給的 tree 假想為一個完滿二元樹，如下圖:

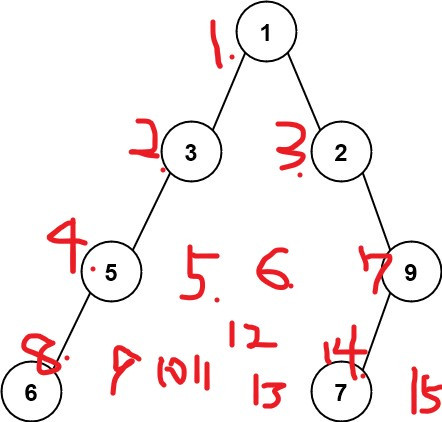
並依序將節點從上而下，由左至右給予編號，這樣某節點編號為 i 時，其左子節點編號為 2*i，其右子節點編號為 2*i + 1。依照這個特性，同層非 null 的節點，取出最右邊的編號減掉最左邊的編號再加一，就有機會得出最長寬度。

例如圖中節點 7 編號為 14，節點 6 編號為 8，14 - 8 + 1 就是所有層數中找到的最大寬度 7。

(6,null,null,null,null,null,7)

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(n)

參考資料