543. Diameter of Binary Tree

解題程式碼

var diameterOfBinaryTree = function(root) {
  let diameter = 0;

  const DFS = (node) => {
    if (!node) return 0;

    let left = DFS(node.left);
    let right = DFS(node.right);
    diameter = Math.max(diameter, left + right);
    return 1 + Math.max(left, right);
  }

  DFS(root);
  return diameter;
};

解題思路、演算法

題目提到重要的一點是最長的路徑不一定會通過整個二元樹的根節點，所以也有可能樹長這樣:

              1
          2      3
       4    5
     6        7

1. 找出右邊、左邊子樹的最長，diameter 為左長 + 右長
2. 每次找到左右子樹長度和後都和前目前 diameter 做比較，找最大值儲存
3. 找到底時，回傳最長值

解法的時間、空間複雜度

時間複雜度: O(n)，每個節點都經過一次
空間複雜度: O(n)，樹的高度

參考資料

leetcode 中文 | Diameter of Binary Tree | Tree Depth First Search 基礎概念 5 - 臉書考題 LeetCode 543.

199. Binary Tree Right Side View

解題程式碼

var rightSideView = function (root) {
  const DFS = (node, height) => {
    if (!node) return;

    nodes[height] = node.val;
    DFS(node.left, height + 1);
    DFS(node.right, height + 1);
  };

  let nodes = [];
  DFS(root, 0);

  return nodes;
};

解題思路、演算法

一開始被題目誤導，以為是取整個樹的右節點及其各層子樹的右節點，但這題是 medium，應該沒那麼簡單，所以實際上是取出整個 tee 各層的右節點，所以左子樹比右子樹層數多，就會取到左子樹的節點，範例圖中，若 8 節點不存在，就會取到 7 節點。

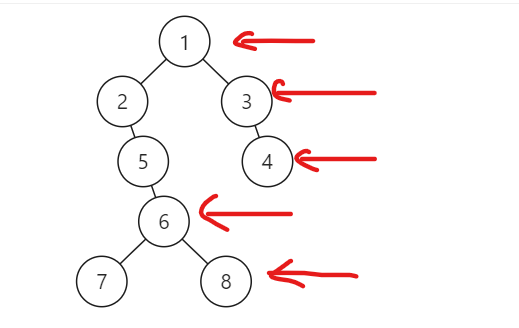
這題的解法，可以使用 Queue 逐漸彈出上層節點，並一一的暫存起當前 BFS 同層的所有節點，而最後一個加入節點，也就是最右邊的節點，其值可以加入到最終結果陣列，到下層節點時，取當前 queue 長度，再以前面的邏輯遍歷一次。

而我在解答區看到一個可以不用 Queue 的作法，因為只需要儲存最右邊的節點，所以指定當前某層 height 為最終結果陣列的索引，然後 BFS 各層節點，左子樹先做 BFS，右子樹後做 BFS，然後各層找到的節點依序重複覆蓋掉最終結果陣列中當前索引的值，就能保證取出的是最右邊的節點。

https://leetcode.com/problems/binary-tree-right-side-view/solutions/549960/javascript-52ms-dfs/

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(n)

參考資料

Binary Tree Right Side View - Breadth First Search - Leetcode 199

104. Maximum Depth of Binary Tree

解題程式碼

var maxDepth = function (root) {
  function DFS(node) {
    if (node === null) return 0;
    return 1 + Math.max(DFS(node.left), DFS(node.right));
  }

  return DFS(root, 0);
};

解題思路、演算法

分別用遞迴找出根節點的左右子樹的深度，取最大值，+1 是計算每遞迴一次，就代表深度會加一

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(1)

參考資料