大家好，今天要來分享union-find，這個主題可以歸類於Graph的演算法，最為人常知的應用在找出圖中是否有cycle或是有幾個connected component，或著任何可以以adjacency list表示的關係想要合併時。

觀念

首先我們有一張兩個component的Graph，並且利用list:[a, b]來表示a和b節點之間有一條相連的連結。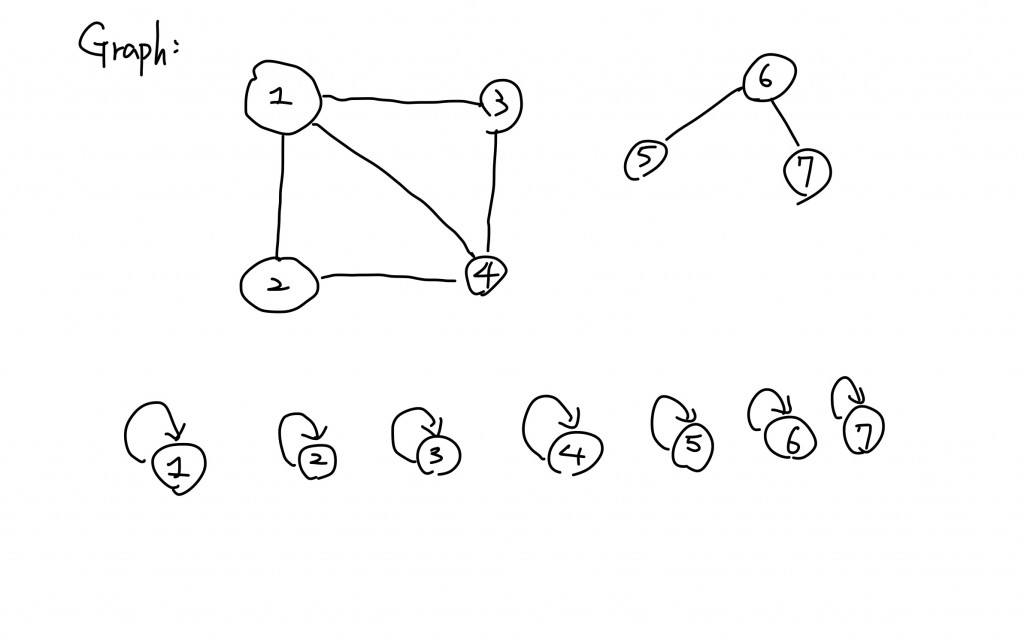

我們要製作一個類別裡面有2個hashmap一個去紀錄每個節點的的父節點，一個去紀錄每個節點目前的高度。
在初始時，每個節點的父節點是自己（指向自己），並且高度為1。在那之後我們去依序拜訪圖裡面的連結。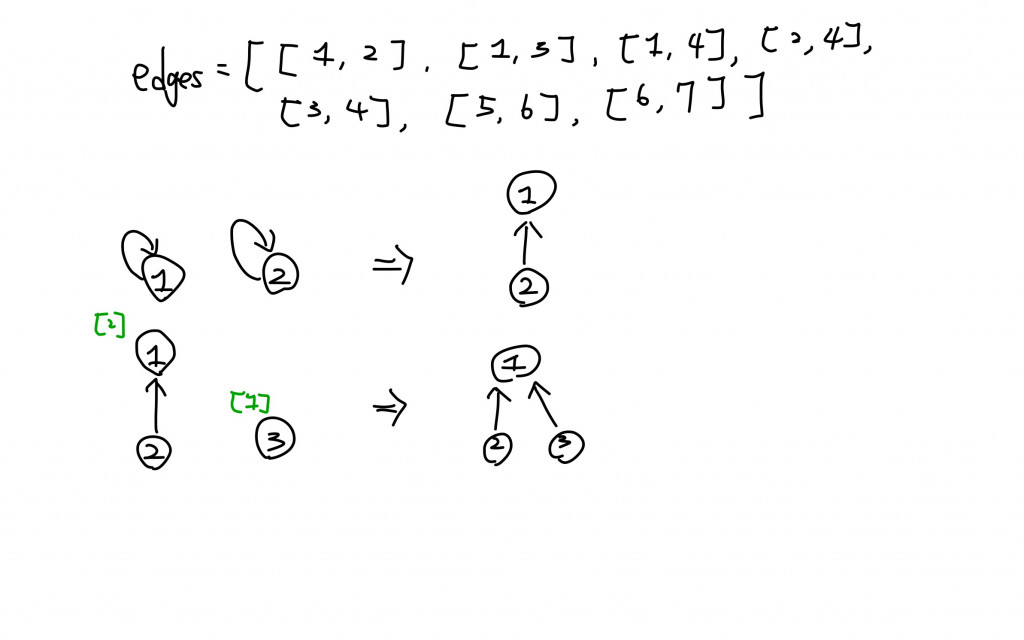

我們根據每個連結中的兩個節點去將這兩個節點合併(Union)，在合併之前我們要先去找到這個節點的"Root"，因為這些要合併的資料結構可以看成是樹。然後我們會去判斷誰的Root高度比較高，比較矮的那一方會被合併在比較高的Root底下成為一棵subTree，這種方式的合併稱為：Union by Rank，這樣在合併後可以維持比較平衡的樹狀資料結構。之後我們要去access到Root的時候會比較有效率。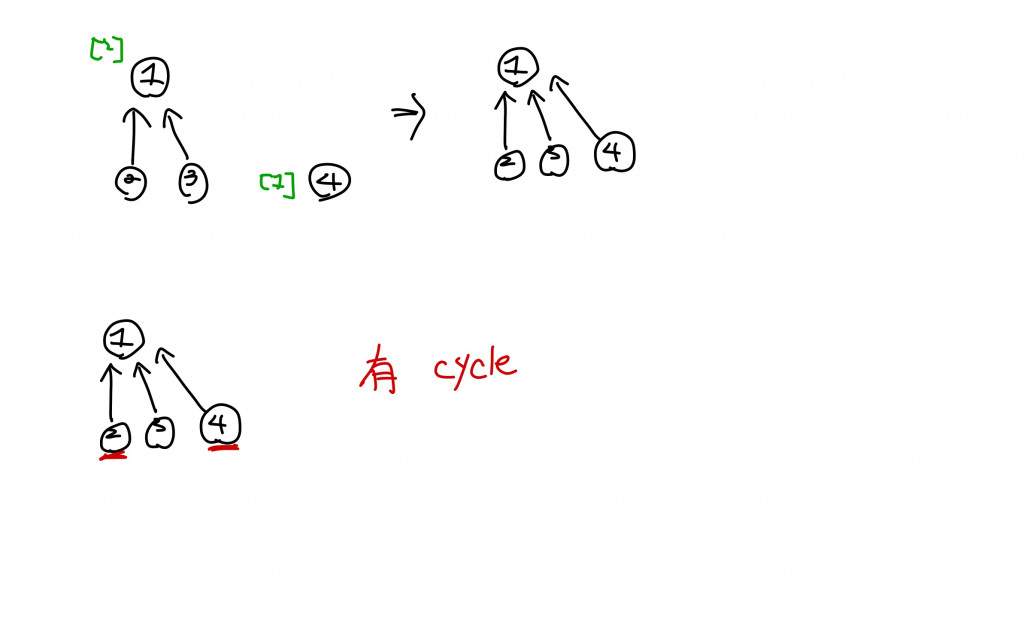

另外在合併時，若發現兩個節點要去尋找的Root是同一個代表存在cycle，所以就不會繼續合併的動作。

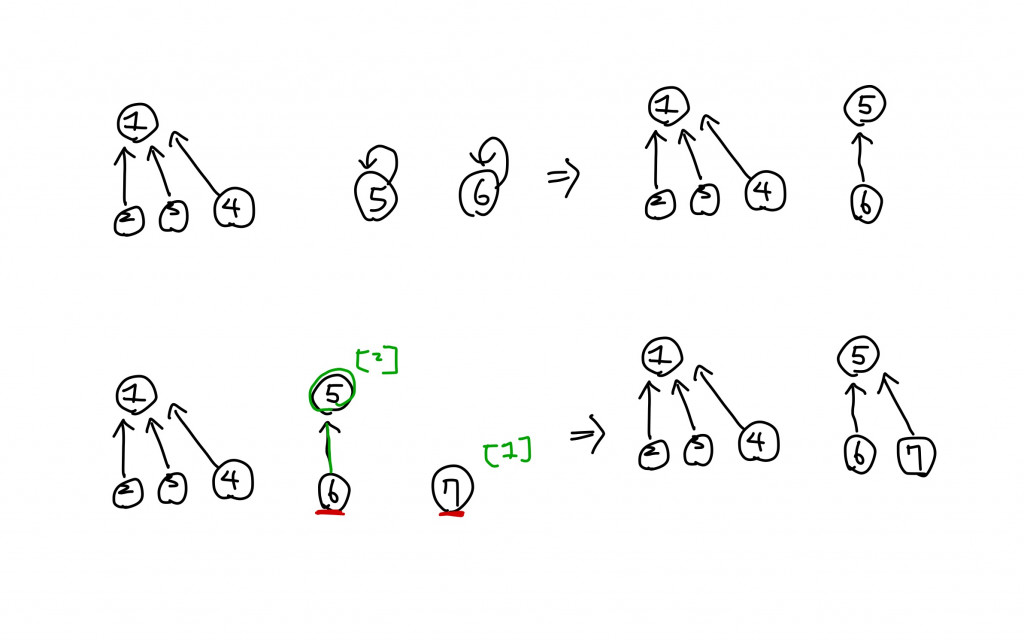
在做完所有的合併動作後，會發現只有兩個樹狀結構，代表這張Graph中有兩個connected component。
所有的節點的Root只會是1或5。

優化與程式碼

我們在尋找Root的過程會利用"find"這個函數來實現。在尋找的過程中我們可以讓節點原先是指著他的父節點改成指向父節點的父節點（就是指向爺爺節點啦）來加速之後再次搜尋Root的速度。稱為：Path Compression。

lass UnionFind:
    def __init__(self, n):
        self.par = {}
        self.rank = {}
        for i in range(1, n + 1):
            self.par[i] = i
            self.rank[i] = 1
        
    
    def find(self, node):
        p = self.par[node]
        while p != self.par[p]:
            self.par[p] = self.par[self.par[p]] # path compression
            p = self.par[p]

        return p
    
    def union(self, n1, n2):
        p1, p2 = self.find(n1), self.find(n2)

        if p1 == p2:
            return False
        
        # union by rank
        if self.rank[p1] > self.rank[p2]:
            self.par[p2] = p1
        elif self.rank[p1] < self.rank[p2]:
            self.par[p1] = p2
        else:
            self.par[p2] = p1
            self.rank[p1] += 1
        
        return True

Leetcode 684. Redundant Connection

題目敘述：有一Tree但多加了一條連結(edge)所形成的無向圖，總共有n個節點，節點以1~n+1編號。並且有n條edge，edge以[a,b]表示並裝在edges中。找出多餘的那條連結。如果有多種答案依edges中最後面的候選edge為答案。

Example1: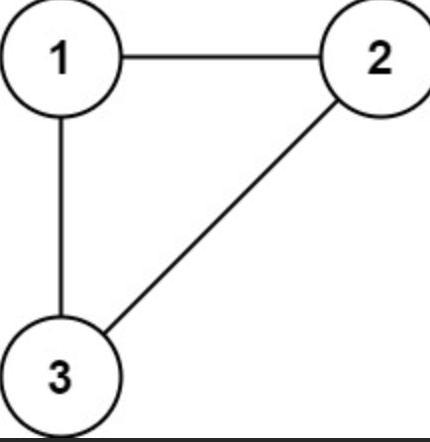

Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

分析：n個節點若有n條edge就會造成迴圈，利用Union Find去依序合併edge來看看到了哪條edge時會造成cycle。

class UnionFind:
    def __init__(self, n):
        self.par = {}
        self.rank = {}
        for i in range(1, n + 1):
            self.par[i] = i
            self.rank[i] = 1
        
    
    def find(self, node):
        p = self.par[node]
        while p != self.par[p]:
            self.par[p] = self.par[self.par[p]]
            p = self.par[p]

        return p
    
    def union(self, n1, n2):
        p1, p2 = self.find(n1), self.find(n2)

        if p1 == p2:
            return False
        
        if self.rank[p1] > self.rank[p2]:
            self.par[p2] = p1
        elif self.rank[p1] < self.rank[p2]:
            self.par[p1] = p2
        else:
            self.par[p2] = p1
            self.rank[p1] += 1
        
        return True

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        ufObj = UnionFind(len(edges))

        for edge in edges:
            if not ufObj.union(edge[0], edge[1]):
                return edge

Leetcode 323. Number of Connected Components in an Undirected Graph

題目敘述：給予一張無向圖，算出圖中共有幾個connected component。

Example: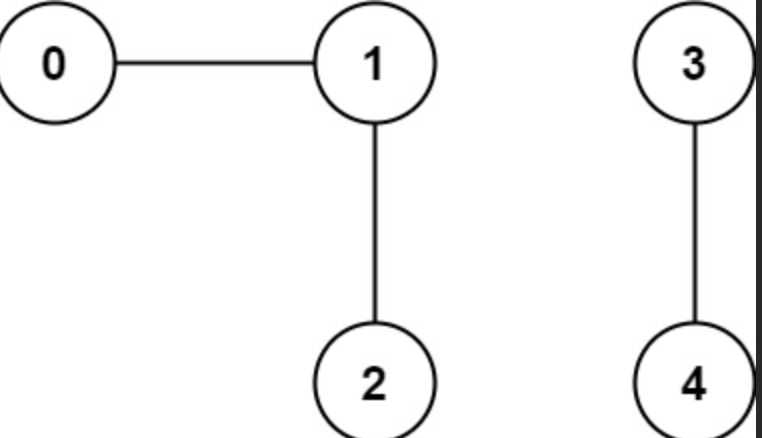

Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2

分析：先對所有edge進行合併。之後再針對每個節點去尋找他們所指向的root。

class UnionFind:
    def __init__(self, n):
        self.par = [i for i in range(n)]
        self.rank = [1] * n
    
    def find(self, x):
        p = self.par[x]
        while p != self.par[p]:
            self.par[p] = self.par[self.par[p]]
            p = self.par[p]
        
        return p
    
    def union(self, x1, x2):
        y1, y2 = self.find(x1), self.find(x2)

        if y1 == y2:
            return False
        
        if self.rank[y1] > self.rank[y2]:
            self.par[y2] = y1
        elif self.rank[y1] < self.rank[y2]:
            self.par[y1] = y2
        else:
            self.par[y2] = y1
            self.rank[y1] += 1

class Solution:
    def countComponents(self, n: int, edges: List[List[int]]) -> int:
        uf = UnionFind(n)
        for u, v in edges:
            uf.union(u, v)
        
        root = set()
        for i in range(n):
            r = uf.find(i)
            root.add(r)
        
        return len(root)

基礎篇結束，明天來分享進階題。