iT邦幫忙

2023 iThome 鐵人賽
DAY 26
0
Software Development

那些前端不用會，但是可以會的資料結構與演算法系列 第 26 篇

【回溯法】Backtracking (1)

15th鐵人賽 回溯法 backtracking
681 瀏覽

  • 分享至 

  • xImage
    •  

本文同步更新於個人網站中，有更好的排版和程式碼區塊 highlighting 支援。

回溯法（backtracking）是一種在某個集合求其子集或特定排列的特殊解法。它沒有對應的資料結構，但其在求解的過程是固定的，它的核心思想是從一個初始狀態開始，暴力搜尋所有可能的解，如果發現不是正確的解，就回溯到上一步，再繼續搜尋，直到找到正確的解或是所有可能的解都已經試過為止。我們這裡所說的集合，通常是指二維陣列、多維陣列或是字串，我們需要從中找到一些符合條件的元素放到結果集中，這是一個嘗試或者說試探的過程。而試探，就會有失敗的情況，如何做到只改些許參數，就能夠繼續試探是非常重要的課題。

我們通常會採用深度優先搜尋（DFS）來遍歷解空間，在介紹二元樹的前、中、後序走訪時也是使用 DFS，因此我們會借助遞迴來完成我們的回溯法。

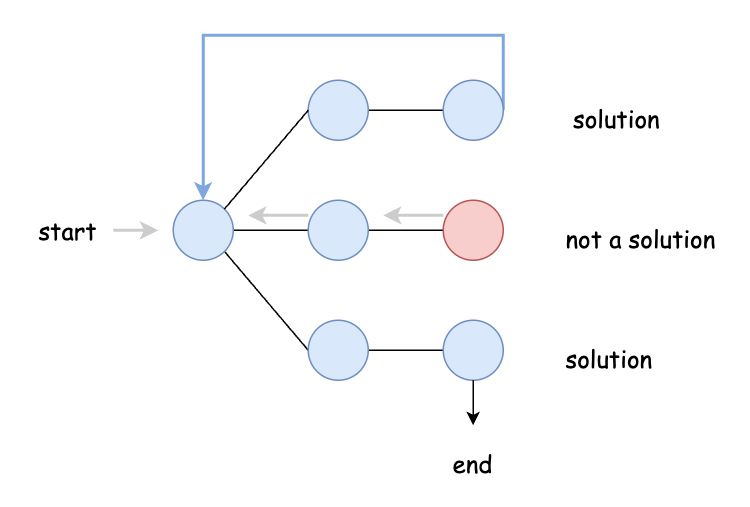
https://ithelp.ithome.com.tw/upload/images/20231011/20152758VxVVIuHMJW.png

回溯法的格式

backtracking 由兩個部分組成：入口函式和遞迴函式（backtrack）。

入口函式分成幾個部分，首先是對參數的簡單判斷，如果不符合條件，立即回傳空結果集。其次是變數的集中定義區域，結果集與候選集（candidates）就是定義在這裡；通常還會對目前集合進行排序，提升程式的效能；如果要對結果進行去重，去重用的 hash 也會放在這裡。然後是呼叫遞迴函式，最後回傳結果集。

遞迴函式一般命名為 backtrack，它分成兩部分，一個是終止條件，應該放在最前面，用於將 candidate 複製一份加入結果集中。為什麼要複製呢？因為我們的結果集通常是一個二維陣列，而 candidate 在遞迴過程滿足特定條件會增加新元素，因此這不能是一個全新的空 candidate。candidate 都是基於某一個有效的 candidate 進行修改（回溯）的。再來談終止條件，它可能是 candidate 的長度是否達到某個臨界值，或者是否已經到達最後一個元素。遞迴函式的第二個部分是進行 for 迴圈，跑迴圈的過程中要收集元素到 candidate，呼叫遞迴函式，因為迴圈過程中的參數是不斷變化的，這樣我們就實現了類似窮舉的效果。在呼叫完遞迴函式後，記得要將一些中間變數還原，變數還原就是回溯的真諦。

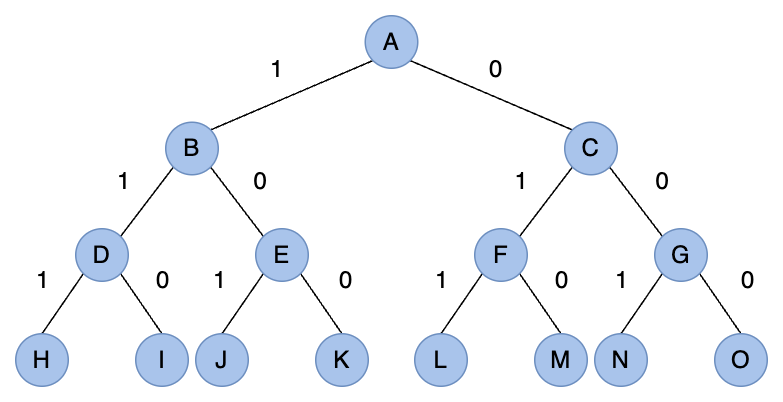
當所給問題是從 n 個元素的集合 S 中找出滿足某個性質的子集時，對應的解空間樹稱為子集樹。例如 n 個物品的 0/1 背包問題（如下圖）所對應的解空間樹是一棵子集樹，這類子集樹通常有 https://chart.googleapis.com/chart?cht=tx&chl=2%5En 個葉節點，節點總數為 https://chart.googleapis.com/chart?cht=tx&chl=2(n%2B1)-1。遍歷子集樹的演算法需要 https://chart.googleapis.com/chart?cht=tx&chl=O(2%5En) 的時間。

https://ithelp.ithome.com.tw/upload/images/20231011/20152758aYUqmxUpOE.png

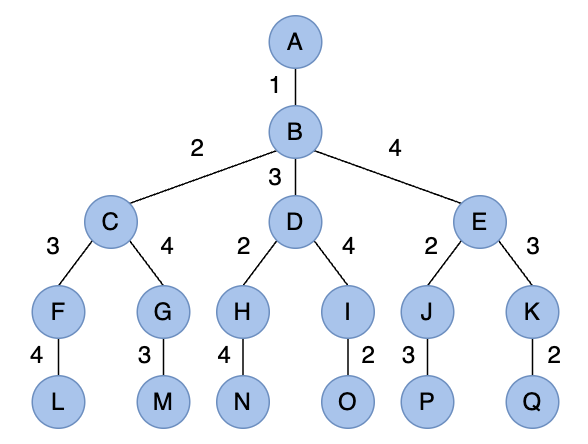
當所給問題是確定滿足某種性質的 n 個元素排列時，對應的解空間樹稱為排列樹。例如旅行推銷員問題（如下圖）的解空間樹是一棵排列樹，這類排列樹通常有 https://chart.googleapis.com/chart?cht=tx&chl=n! 個葉節點。遍歷子集樹的演算法需要 https://chart.googleapis.com/chart?cht=tx&chl=O(n!) 的時間。

https://ithelp.ithome.com.tw/upload/images/20231011/20152758EdcKJSaHvh.png

backtracking 的 pseudocode 如下：

// 子集樹
function main(set, 其他參數) {
  if (如果 set 不合法或長度為零，或其他參數明顯有問題) {
    return 簡單結果;
  }
  set.sort(); // 排序提升效率
  let result = [], candidate = [], end = nums.length;

  function backtrack(start, 其他參數) {
    if (start === end) { // 或其他情況
      // 這裡可能還有其他條件
      result.push([...candidate]); // 將候選集複製一份加入結果集
    } else {
      // 注意，如果限定子集數量需要改動一下
      for (let i = start; i < end; i++) {
        // 處理中間變數
        candidate.push(陣列元素);
        backtrack(i + 1, ...);
        candidate.pop(); // 還原 candidate
        // 還原其他中間變數
      }
    }
  }

  backtrack(0, 其他參數);
  return result;
}

// 排列樹
function main(set, 其他參數) {
  if (如果 set 不合法或長度為零，或其他參數明顯有問題) {
    return [];
  }
  // set 不需要排序！
  let result = [], candidate = [], end = nums.length, hash = {};
  // hash 是用來實現排序效果的
  function backtrack(start, 其他參數) {
    if (start === end) { // 或其他情況
      // 這裡可能還有其他條件
      result.push([...candidate]);
      return;
    }
    for (let i = 0; i < end; i++) {
      // 處理中間變數
      if (!hash[i]) {
        hash[i] = true;
        candidate.push(陣列元素);
        backtrack(start + 1, ...);
        candidate.pop(); // 還原 candidate
        hash[i] = false;
        // 還原其他中間變數
      }
    }
  }

  backtrack(0, 其他參數);
  return result;
}

子集問題的相關題目

子集問題的相關例題包括沒重複元素的子集問題、有重複元素的子集問題、有重複元素的組合總和、背包問題、裝載問題和火柴棒問題等。

沒重複元素的子集問題

這是 LeetCode 78. Subsets 的原題，給定一個不包含重複元素的整數陣列 nums，回傳該陣列所有可能的子集（幂集）。注意：結果集不能包含重複的子集。

Example 1:

Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Example 2:

Input: nums = [0]
Output: [[],[0]]

思路：我們根據上面的 pseudocode 來實現，首先是入口函式的第一部分，怎麼快速排除有問題的參數或特例。如果參數不是陣列或是它的長度為零，我們就直接回穿空陣列。然後我們宣告一個 result、candidate，排序陣列，然後呼叫遞迴函式。

接下來我們看一下終止條件，因為子集可以為空，也就是說任何情況 candidate 都可以放進 result。其他就與模板一致了。我們來看一下實作程式碼：

function subsets(nums) {
  if (!Object(nums).length) { // 相當於 !nums || !nums.length
    return [];
  }

  nums.sort((a, b) => a - b);
  const result = [];
  const candidate = [];
  const end = nums.length;

  function backtrack(start) {
    result.push([...candidate]); // 沒有長度限制，直接放進 result

    for (let i = start; i < end; i++) {
      candidate.push(nums[i]); // 試探
      backtrack(i + 1); // 修改參數
      candidate.pop(); // 不管成功與否，退回上一步
    }
  }

  backtrack(0);
  return result;
}

整個探索過程如下：

https://chart.googleapis.com/chart?cht=tx&amp;chl=i candidate result
0 [1] [[], [1]]
1 [1, 2] [[], [1], [1, 2]]
2 [1, 2, 3] [[], [1], [1, 2], [1, 2, 3]]
2 [1, 3] [[], [1], [1, 2], [1, 2, 3], [1, 3]]
1 [2] [[], [1], [1, 2], [1, 2, 3], [1, 3], [2]]
2 [2, 3] [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3]]
2 [3] [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]

有重複元素的子集問題

如果今天給定的陣列存在重複元素呢？我們再來看看 90. Subsets II 的原題，給定一個可能包含重複元素的整數陣列 nums，回傳該陣列所有可能的子集（幂集）。注意：結果集不能包含重複的子集。

Example 1:

Input: nums = [1,2,2]
Output: [[],[1],[1,2],[1,2,2],[2],[2,2]]

Example 2:

Input: nums = [0]
Output: [[],[0]]

與上一題只有一點差別，但它只是對候選集做出限制，即結果集中不能出現兩個 [1,2] 陣列。

我們可以使用 hash 來去重，實作程式碼如下：

function subsetsWithDup(nums) {
  nums.sort((a, b) => a - b);
  const result = [];
  const candidate = [];
  const end = nums.length;
  const hash = new Map();

  function backtrack(start) {
    const candidateKey = candidate.toString();
    if (!hash.get(candidateKey)) { // 去除重複
      result.push([...candidate]);
      hash.set(candidateKey, true);
    }
    for (let i = start; i < end; i++) {
      candidate.push(nums[i]);
      backtrack(i + 1);
      candidate.pop();
    }
  }

  backtrack(0);
  return result;
}

當然，我們也可以在遞迴函式的 for 迴圈中加入判斷去重，有興趣的讀者可以嘗試一下。

有重複元素的組合總和

這題是 39. Combination Sum 的原題，給定一個無重複元素的正整數陣列 candidates 和一個正整數 target，找出 candidates 中所有可以使數字之和為 target 的組合。candidates 中的數字可以無限制重複被選取。

Example 1:

Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]

Example 2:

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

Example 3:

Input: candidates = [2], target = 1
Output: []

思路：本題更接近我們的模板，由於元素可以重複使用，我們在遞迴函式的 for 迴圈裡就不用改變 start 變數。並且我們還要計算放入候選集的元素的總和是否為 target，但總不能每次都把候選集加總一次吧，反過來，我們每次將它與新元素相減，只要結果為零，就退出遞迴。實作程式碼如下：

function combinationSum(candidates, target) {
  const result = [];
  const combination = [];
  const end = candidates.length;

  function backtrack(start, target) {
    if (target === 0) { // 等於 0，退出遞迴
      result.push([...combination]);
      return;
    }
    if (target > 0) { // 大於 0，繼續新增元素
      for (let i = start; i < end; i++) {
        combination.push(candidates[i]);
        // 注意這裡 i 沒有加 1，因為可以重複使用相同的數字
        backtrack(i, target - candidates[i]);
        combination.pop();
      }
    }
  }

  backtrack(0, target);
  return result;
}

無重複元素的組合總和

這題是 40. Combination Sum II 的原題，給定一個元素範圍為 1~50 的整數陣列和一個目標數字 target，找出陣列中所有可以使數字之和為 target 的組合。陣列中的每個數字只能在組合中使用一次。結果集不能包含重複的組合。

Example 1:

Input: candidates = [10,1,2,7,6,1,5], target = 8
Output: [[1,1,6],[1,2,5],[1,7],[2,6]]

Example 2:

Input: candidates = [2,5,2,1,2], target = 5
Output: [[1,2,2],[5]]

思路與上面很相似，但由於元素只使用一次，我們只要在迴圈中改變 start 的值即可。並且題目要求結果集不能包含重複的組合，解決方案一樣是使用 hash 去重。實作程式碼如下：

function combinationSum2(candidates, target) {
  candidates.sort((a, b) => a - b);
  const result = [];
  const combination = [];
  const end = candidates.length;
  const hash = {};

  function backtrack(start, target) {
    const combinationKey = combination.toString(); // 將陣列轉為字串當作 key
    if (target === 0 && !hash[combinationKey]) {
      result.push([...combination]);
      hash[combinationKey] = true;
      return;
    }

    if (target > 0) {
      for (let i = start; i < end; i++) {
        combination.push(candidates[i]);
        backtrack(i + 1, target - candidates[i]);
        combination.pop();
      }
    }
  }

  backtrack(0, target);
  return result;
}

0/1 背包問題

給定 n 個重量為 https://chart.googleapis.com/chart?cht=tx&amp;chl=w_1%2C%20w_2%2C%20...%2C%20w_n，價值為 https://chart.googleapis.com/chart?cht=tx&amp;chl=v_1%2C%20v_2%2C%20...%2C%20v_n 的物品和一個容量為 capacity 的背包，求如何裝才能在不超過背包承重的情況下，使得背包中物品的總價值最大？

Example:

input: n = 5, [2, 2, 6, 5, 4], [6, 3, 5, 4, 6], capacity = 10
output: 15, [1, 1, 0, 0, 1] // 1 表示選取，0 表示不選取

0/1 背包問題的解題思路在於遞迴函式的 for 迴圈，其 end 變數不再是物品的數量，而是我們決策分支的數量、選還是不選。因此 end = 1（從零開始），然後我們設計一個陣列，來記錄該物品的選擇情況。由於限制條件存在兩個，首先是放進背包的總重量不能超過背包的容量，因此我們需要不斷累計這個變數。其次，當選擇最後一個物品後，我們要看物品的總價值是否比之前的還高。實作程式碼如下：

function knapsack01(n, weights, values, capacity) {
  const allocation = new Array(n).fill(0); // 表示是否選中
  let currValue = 0;
  let currWeight = 0;
  let maxValue = 0;
  let maxWeight = 0;
  let result = [];

  function backtrack(start) {
    if (start === n && currValue > maxValue) {
      maxValue = currValue;
      maxWeight = currWeight;
      result = [...allocation];
      return;
    }

    for (let i = 0; i < 2; i++) {
      if (currWeight + i * weights[start] <= capacity) {
        allocation[start] = i; // 0 為不放進包中，1 為放進包中
        currWeight += i * weights[start];
        currValue += i * values[start];
        backtrack(start + 1);
        currWeight -= i * weights[start];
        currValue -= i * values[start];
      }
    }
  }

  backtrack(0);
  return [maxValue, result];
}

裝載問題

有 n 個集裝箱要裝上兩艘輪船，兩艘輪船的載重分別為 c1 和 c2。其中每個集裝箱的重量為 [w0, w1, ..., wi]，請問是否有一個合理的裝載方案，可將這 n 個集裝箱裝上兩艘輪船？

如果有，請給出一個裝載方案。

Example 1:

input: c1 = 50, c2 = 50, goods = [10, 40, 40]
output: [[10, 40], [40]]

Example 2:

input: c1 = 50, c2 = 50, goods = [20, 40, 40]
output: [[], []]

思路：這題與 0/1 背包問題很相似，只不過上一題是放到一艘船（包）上，這題是放到兩艘船上。在之前的題型中，我們不知道結果集中有多少個子陣列，現在我們明確知道有兩個，我們可以直接生成所有子陣列。然後在遞迴函式的迴圈中，根據子陣列的總和依次判定是否能繼續放東西。實作程式碼如下：

function boatLoad(c1, c2, goods) {
  goods.sort();
  const boats = [[], []];
  const currWeight = [0, 0];
  const maxWeight = [c1, c2];

  function backtrack(start) {
    if (start >= goods.length) {
      return currWeight[0] <= maxWeight[0] && currWeight[1] <= maxWeight[1];
    } else {
      const weight = goods[start];
      for (let i = 0; i < 2; i++) {
        if (currWeight[i] + weight > maxWeight[i]) {
          continue;
        }

        currWeight[i] += weight;
        boats[i].push(weight);

        if (backtrack(start + 1)) {
          return true;
        }

        currWeight[i] -= weight;
        boats[i].pop();
      }
    }
    return false;
  }

  backtrack(0);
  return boats;
}

火柴棒拼出正方形

給定一個整數陣列 matchsticks，裡面的數字代表該個火柴棒的長度，求解是否能將這些火柴棒拼成一個正方形？例如 [4, 3, 3, 2, 2, 1, 1] 能拼成如下圖所示的正方形：

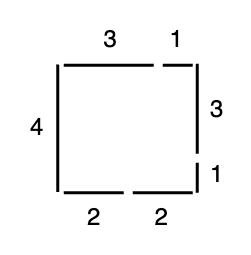
https://ithelp.ithome.com.tw/upload/images/20231011/20152758W8M56asZCp.png

思路：既然是正方形，那肯定有四條邊，因此陣列中的元素不能少於 4 個，且每條邊的長度必須相等，換言之，所有元素的總和必須是 4 的倍數。這樣一來我們就可以輕鬆排除一些不合法的參數。然後進入探索過程，這和裝載問題差不多，不同的是我們需要 4 個子陣列。實作程式碼如下：

function makesquare(matchsticks) {
  if (matchsticks.length < 4) {
    // 如果火柴棒數量小於 4，則無法構成正方形
    return false;
  }

  const sides = [[], [], [], []]; // sides 是用來觀察每個邊的火柴棒的，可以不要有
  const total = matchsticks.reduce((acc, curr) => acc + curr, 0);

  if (total % 4) {
    // 不能被 4 整除
    return false;
  }

  matchsticks.sort((a, b) => b - a); // 由大到小排序
  const maxSideLength = total / 4;
  const currSide = [0, 0, 0, 0];
  const end = matchsticks.length;

  function backtrack(start) {
    if (start >= end) {
      return (
        currSide[0] === maxSideLength &&
        currSide[1] === maxSideLength &&
        currSide[2] === maxSideLength &&
        currSide[3] === maxSideLength
      );
    } else {
      for (let i = 0; i < 4; i++) {
        if (currSide[i] + matchsticks[start] > maxSideLength) {
          continue;
        }

        sides[i].push(matchsticks[start]); // 這個可以不要
        currSide[i] += matchsticks[start];

        if (backtrack(start + 1)) {
          return true;
        }

        sides[i].pop(); // 這個可以不要
        currSide[i] -= matchsticks[start];
      }
    }
    return false;
  }

  const result = backtrack(0);
  console.log(JSON.stringify(sides), result);
  return result;
}

小結

我們今天認識了回溯法的基本概念，並利用模板來實際練習了很多子集相關的題目，明天還會繼續來看看排列相關的題目。

參考資料


上一篇
【隨機演算法】Fisher-Yates Shuffle
下一篇
【回溯法】Backtracking (2)
系列文
那些前端不用會，但是可以會的資料結構與演算法 共 31 篇
  1. 27
    【回溯法】Backtracking (2)
  2. 28
    【動態規劃】Dynamic Programming (1)
  3. 29
    【動態規劃】Dynamic Programming (2)
  4. 30
    【貪婪演算法】Greedy Algorithm
  5. 31
    完賽雜談
完整目錄
圖片
  直播研討會
圖片
{{ item.channelVendor }} {{ item.webinarstarted }} |
{{ formatDate(item.duration) }}
直播中

尚未有邦友留言

立即登入留言
iThome鐵人賽
參賽組數
1064 組
團體組數
40 組
累計文章數
22195 篇
完賽人數
600 人
iT+看影片追技術 看影片追技術 看更多
熱門tag 看更多
15th鐵人賽 16th鐵人賽 13th鐵人賽 14th鐵人賽 12th鐵人賽 11th鐵人賽 鐵人賽 2019鐵人賽 javascript 2018鐵人賽 python 2017鐵人賽 windows php c# windows server linux css react vue.js
熱門問題
熱門回答
熱門文章
IT邦幫忙