簡介

Scikit-learn 的 cheatsheet 中列出了多種常用的回歸算法，包括：Lasso Regression、Ridge　Regression、ElasticNet Regression、SVR、Ensemble Regressors、SGD Regressor。

對於每種演算法，我們今天將從以下幾個方面進行介紹：

• 🔍基本原理🔍：簡要說明演算法的核心思想
• ⚠️注意事項⚠️：提醒使用該演算法時需要注意的問題

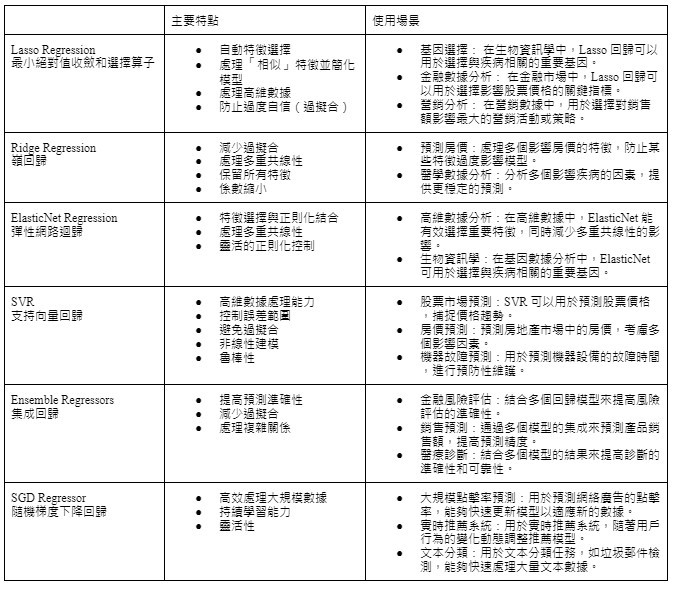
並且將主要特點及使用場景整理成表格圖供比較。

［自製梗圖］

Cheatsheet 中的演算法介紹 - 回歸

回歸模型試圖找出自變量（特徵）與因變量（目標）之間的關係，並基於這些關係進行預測。以下是 scikit-learn cheatsheet 提及的回歸演算法：

1. Lasso Regression (Least Absolute Shrinkage and Selection Operator，最小絕對值收斂和選擇算子)

• 🔍基本原理🔍：Lasso 回歸是一種特殊的線性回歸方法。線性回歸就像是試圖用一條直線來描述數據點的關係。而 Lasso 不僅要找到這條最佳的直線，還要決定哪些特徵是真正重要的。Lasso 回歸的基本思想是，基於普通線性回歸基礎上添加了 L1 範數正則化將某些特徵的係數縮減為零來選擇最重要的特徵，從而簡化模型並提高其泛化能力。這個正則化項是係數的絕對值之和。想像你在縮小一張圖片，Lasso就像是把一些不重要的細節完全去掉，只保留最關鍵的部分。

L1 範數是一種計算向量各個分量絕對值總和的方式。對於回歸模型來說，L1 範數正則化會將回歸係數的絕對值總和作為懲罰項，加入到損失函數中。這樣，模型會傾向於將一些係數縮減為零，從而進行特徵選擇。

• ⚠️注意事項⚠️：
  • 多重共線性：當特徵之間存在高度相關性時，Lasso 回歸可能會隨機選擇其中一個特徵，而忽略其他同樣重要的特徵。這時，可以考慮使用 ElasticNet 回歸來解決這個問題。
  • 對特徵的尺度敏感，通常需要標準化：在使用Lasso之前，我們需要將所有特徵調整到相同的尺度，否則，某些特徵可能僅僅因為它們的數值較大而被錯誤地認為更重要。
  • 參數調整：Lasso 的正則化強度由參數 α 控制，需要通過反覆試驗不同的 α 值來找到最佳平衡點。這就像決定整理衣櫃的嚴格程度，過於寬鬆可能留下過多不需要的特徵，而過於嚴格則可能丟失一些重要特徵。

2. Ridge Regression（嶺回歸）

• 🔍基本原理🔍：Ridge 回歸是另一種線性回歸方法，他在基於普通線性回歸基礎上添加了 L2 範數正則化來限制回歸係數的大小。這個正則化項是係數平方和。如果說 Lasso 是完全去掉一些特徵，那麼 Ridge 就像是把所有特徵都保留，但是減弱它們的影響力。L2 範數正則化會對回歸係數的平方和進行懲罰，有助於減少模型的複雜度，從而提高模型的穩定性。

L2 範數是一種計算向量各個分量平方和的平方根的方式。對於回歸模型來說，L2 範數正則化會將回歸係數的平方和作為懲罰項，加入到損失函數中，這樣模型會傾向於使所有係數的大小都比較小。

• ⚠️注意事項⚠️：
  • 需要標準化特徵：在使用 Ridge 回歸之前，通常需要對特徵進行標準化。
  • 參數調整：Ridge 回歸的正則化強度由參數 λ 控制，需要通過交叉驗證來選擇最佳的 λ 值。

3. ElasticNet Regression（彈性網路迴歸）

• 🔍基本原理🔍：ElasticNet 回歸結合了 L1 和 L2 範數正則化，將 Lasso 和 Ridge 回歸的優勢結合在一起。它既能進行特徵選擇，又能限制回歸係數的大小，有助於處理多重共線性問題。
• ⚠️注意事項⚠️：
  • 需要標準化特徵：ElasticNet 需要對特徵進行標準化。
  • 參數調整：需要通過交叉驗證選擇最佳的 α 和 λ 值，需要同時調整兩個參數，以平衡特徵選擇和正則化的需求。
  • 計算成本：比單純的 Lasso 或 Ridge 更高。

4. SVR（Support Vector Regression，支持向量回歸）

• 🔍基本原理🔍：支持向量回歸 (SVR) 是將支持向量機 (SVM) 的原理應用到回歸問題上。SVR 透過找到一條能夠盡量包含大部分數據點的最佳超平面來進行回歸。這個最佳超平面會使得大部分數據點落在一個稱為 "epsilon tube (ε)" 的區域內，同時最小化超出這個區域的數據點的誤差。想像你在拉一條橡皮筋通過一群氣球，SVR 就是要找到一條最平滑的橡皮筋路徑，使得盡可能多的氣球都能碰到這條橡皮筋。
• ⚠️注意事項⚠️：
  • 選擇正確的核函數：SVR 的效果依賴於選擇合適的核函數（如線性核、高斯核、多項式核等），需要根據具體問題進行調整。
  • 參數調整：需要通過交叉驗證選擇合適的 C（正則化參數）和 epsilon 值，以達到最佳效果。
  • 計算複雜度：在大數據集上可能會很慢。
  • 需要標準化特徵：SVR 需要對特徵進行標準化。

5. Ensemble Regressors (集成回歸)

• 🔍基本原理🔍：集成回歸通過結合多個回歸模型的預測結果來提高預測準確性和穩定性。這種方法利用多個模型的優勢，減少單一模型的偏差和方差。這就像是在做一個重要決定時，你會詢問多個專家的意見，然後綜合考慮。他與集成分類器一樣有分成三種類型：

Bagging（自助聚集法）：通過多次隨機抽樣生成多個訓練子集，訓練多個基礎模型（如隨機森林），然後將這些模型的預測結果進行平均或投票來得到最終預測。

Boosting（提升法）：通過逐步訓練多個模型，每個模型試圖糾正前一個模型的錯誤。常見的算法有 AdaBoost 和 Gradient Boosting。

Stacking（堆疊法）：通過訓練多個基礎模型，然後用這些模型的預測結果作為新特徵，再訓練一個終極模型來得到最終預測。

• ⚠️注意事項⚠️：
  • 計算成本：訓練和預測時間可能會很長。
  • 解釋性：集成模型通常難以解釋。
  • 參數調優：需要調整的參數較多，增加了複雜度。
  • 模型複雜度：集成方法通常需要較高的計算資源和較長的訓練時間。
  • 過擬合風險：雖然集成方法能夠減少過擬合，但如果基礎模型過多或過於複雜，仍可能出現過擬合現象。

6. SGD Regressor (Stochastic Gradient Descent Regressor，隨機梯度下降回歸)

• 🔍基本原理🔍：隨機梯度下降回歸 (SGD Regressor) 是一種基於梯度下降算法的線性回歸方法。與批量梯度下降不同，SGD 在每次迭代中僅使用一個或一小部分樣本來更新模型參數，這使得其在大規模數據集上的訓練速度更快。它每次只使用一個或一小批樣本來更新模型參數，而不是使用全部數據。這就像是你在爬山，每次只看腳下的一小塊地形來決定下一步往哪走，而不是每次都觀察整個山峰。
• ⚠️注意事項⚠️：
  • 學習率調整：學習率是 SGD 的關鍵參數，過大會導致收斂不穩定，過小則收斂速度慢。需要通過調參找到合適的學習率。
  • 特徵標準化: 由於 SGD 對特徵尺度敏感，通常需要對特徵進行標準化處理。
  • 敏感性：對特徵縮放和學習率的選擇敏感。
  • 收斂性：可能需要多次運行才能達到最佳結果。
  • 隨機性：結果可能會有輕微的隨機性。

結論

這些回歸算法各有特點，適用於不同的場景。在實際應用中，往往需要根據具體問題和數據特性來選擇最合適的算法，有時甚至需要結合多種算法來獲得最佳效果。理解每種算法的原理和特點，將有助於我們在面對實際問題時做出明智的選擇。下一章節將針對 cheatsheet 中的聚類演算法做介紹。