在上一篇文章中，我們探討了如何選擇和應用回歸演算法來預測連續值。今天，我們將轉向無監督學習領域，重點介紹機器學習中的聚類演算法。

簡介

聚類的目標是將數據分成多個組（或稱為「群」，「簇」），「簇」是指一組數據點，它們在某種意義上彼此相似。可以把簇想像成一群相似的物體。例如，在一組積木中，我們可以將所有顏色相同的積木放在一起，這樣每一組積木就是一個簇。簇的內部數據點彼此之間的相似度高，而不同簇之間的數據點則有明顯的區別。聚類演算法的目標就是自動識別和形成這樣的簇。

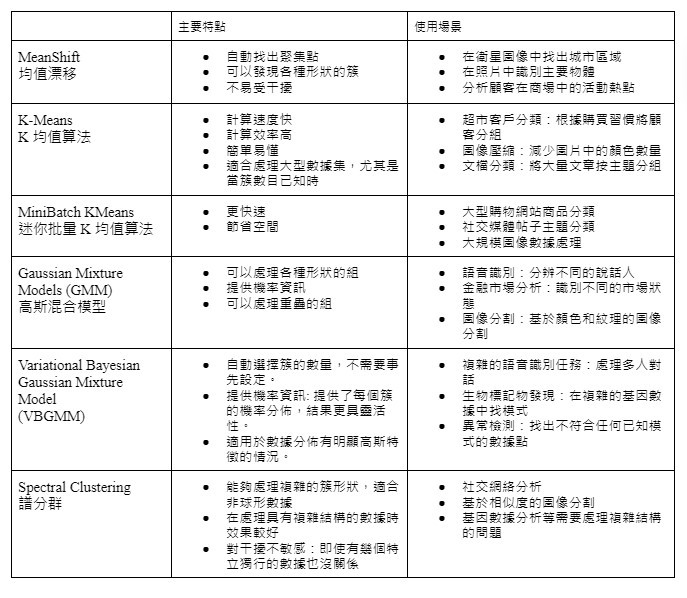
Scikit-learn 提供了一系列的聚類演算法，在這篇文章中，我們將介紹幾種主要的聚類演算法，包括：MeanShift、KMeans、MiniBatch KMeans、Gaussian Mixture Models (GMM)、VBGMM、Spectral Clustering。對於每種演算法，我們今天將從以下幾個方面進行介紹：

🔍基本原理🔍：簡要說明演算法的核心思想
⚠️注意事項⚠️：提醒使用該演算法時需要注意的問題
並且將主要特點及使用場景整理成表格圖供比較。

Cheatsheet 中的演算法介紹- 聚類

聚類演算法不需要標籤數據，而是依據數據本身的特徵進行分類。想像一下，你有一大堆不同顏色、形狀的積木。聚類算法能夠自己將相似的積木分在一起。比如，他可能會把所有的紅色積木放在一起，藍色的放在一起，或者把所有的圓形積木放在一起，方形的放在一起。這就是聚類算法的基本思想：將相似的東西分到一組。

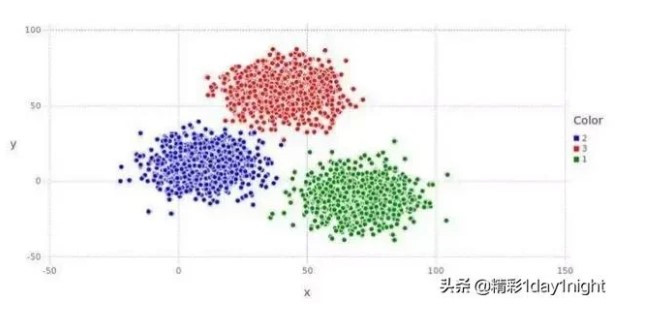
［圖片來源］

以下是 scikit-learn cheatsheet 提及的聚類演算法。

1. MeanShift（均值偏移）

• 🔍基本原理🔍：MeanShift 是一種基於密度的聚類演算法，其主要思想是將數據點移動到其周圍數據點密度最大的區域。具體來說，MeanShift 的運作過程如下：

1) 選擇起點：隨機選擇一個數據點作為起點。

2) 計算密度：計算這個數據點周圍一定範圍內所有數據點的平均位置。

3) 移動：將起點數據點移動到計算出的平均位置。

4) 迭代：重複步驟 2 和 3，直到數據點的移動變得非常微小，達到一個穩定的位置。

5) 這些穩定的位置就形成了簇的中心。

以上如果很難理解的話，也可以想像成你在擁擠的遊樂園中尋找人群聚集處：

1) 隨機選擇位置：在遊樂園中隨便選擇一個位置作為起點。

2) 觀察人群：看看這個位置周圍一定範圍內有多少人。

3) 移動：向人最多的方向移動一小步。

4) 重複：重複步驟 2 和 3，直到你找到人最多的地方。

5) 檢查其他區域：對遊樂園中其他未檢查的區域重複這些步驟。

最終，你會發現遊樂園中有幾個主要的人群聚集處，每個人群就是一個簇。MeanShift 通過這種方式自動識別和形成簇。

• ⚠️注意事項⚠️：
  • 在密度差異大的情況下可能效果不佳
  • 計算量大：對於大規模數據集，MeanShift 的計算量可能較大

2. K-Means（k-均值算法）

• 🔍基本原理🔍：KMeans 是最常見的聚類演算法之一，它的基本思想是將數據點分為 K 個簇，使得每個簇內的數據點與簇中心的距離最小。算法通過以下步驟進行：隨機選擇 K 個簇中心，將每個數據點分配到距離最近的簇中心，然後更新每個簇的中心為簇內數據點的平均位置，直到簇中心不再變化。想像你有一堆不同顏色的彈珠，要將它們分成K堆。K-Means 就是：

1) 隨機選K個位置作為中心點 

2) 將每個彈珠分配到最近的中心點 

3) 重新計算每堆彈珠的中心位置 

4) 重複步驟 2-3 直到中心點不再變化

• ⚠️注意事項⚠️：
  • 需要事先指定簇的數量 K：需要事先明確知道要分幾組
  • 對於簇的形狀和大小有一定的假設：分佈奇怪的形狀不適用此方法，因為不適合所有數據分佈
  • 對初始中心點敏感：開始的選擇會影響最終結果

3. MiniBatch KMeans（迷你批量k-均值算法）

• 🔍基本原理🔍：MiniBatch KMeans 是 KMeans 演算法的一種變形，通過隨機抽取小批量數據進行更新，以提高計算效率。它使用隨機選擇的小批量數據來更新簇的中心，然後用這些更新結果來重新計算整體的簇中心，從而逐步收斂到最優解。想像你要整理一個大房間的玩具，但一次只整理一小部分：

1) 隨機選幾個玩具開始整理

2) 為這些玩具找到最近的堆

3) 更新這些堆的中心位置

4) 重複步驟 1-3，每次選不同的玩具，直到整理完所有玩具

• ⚠️注意事項⚠️：
  • 結果可能稍微不如標準 K-Means 精確，但通常能夠接受
  • 仍需預先決定分幾類
  • 對小數據可能沒優勢：需要選擇合適的批量大小來平衡計算效率和結果準確性

4. Gaussian Mixture Models (GMM, 高斯混合模型)

• 🔍基本原理🔍：Gaussian Mixture Models (GMM) 假設數據點來自多個高斯分佈的混合，每個高斯分佈代表一個簇。算法使用期望最大化方法來估計每個高斯分佈的參數以及每個數據點屬於各個高斯分佈的概率。想像你有一堆不同顏色的氣球，要猜這些氣球來自哪幾個派對：

1) 猜測有幾個派對放飛了氣球

2) 估計每個派對放飛氣球的中心位置和分散程度

3) 計算每個氣球最可能來自哪個派對

4) 根據猜測結果，調整對每個派對的估計

5) 重複步驟 3-4，直到猜測不再有大的變化

• ⚠️注意事項⚠️：
  • 在高維度數據中可能效果不佳：需要選擇合適的高斯分佈數量，過多或過少的分佈數量可能影響結果。
  • 計算過程可能較為複雜，需要多次猜測和調整。
  • 需要設定初始猜測：初始猜測不好可能影響結果，需要初始化參數以提高收斂效果。

5. Variational Bayesian Gaussian Mixture Model (VBGMM)

• 🔍基本原理🔍：VBGMM 是一種基於貝葉斯推斷的高斯混合模型。它假設數據點來自若干個高斯分佈的混合，並使用變分推斷方法來估計這些高斯分佈的參數和數量。與傳統的高斯混合模型（GMM）不同，VBGMM 可以自動決定最佳的簇數，並提供每個簇的概率分佈。GMM的進階版，就像是一個更聰明的氣球派對偵探：

1) 不需要預先猜測派對數量，而是從多個可能的派對數開始

2) 通過複雜的數學方法（變分推斷）來估計最可能的派對數量和特徵

3) 自動調整模型，去除不必要的派對假設

4) 提供每個猜測的不確定性估計

• ⚠️注意事項⚠️：
  • 計算過程更加複雜：需要更多時間來思考和推理，因此需要較長時間來收斂。
  • 對初始設定敏感：起始的想法會影響最終結論，需要合理選擇初始化參數以保證收斂到全局最優解。
  • 解釋結果可能更困難：需要理解機率和不確定性。

6. Spectral Clustering （譜分群）

• 🔍基本原理🔍：Spectral Clustering 基於圖論，通過對數據的相似度矩陣進行特徵值分解來進行聚類。它首先將數據點表示為圖的節點，然後構建相似度矩陣，接著進行特徵值分解，將數據映射到低維空間中，再使用傳統的聚類方法（如 KMeans）進行最終的聚類。想像你要根據朋友關係將班級同學分組：

1) 畫出每個人與其他人的關係圖

2) 將這個複雜的關係圖轉換成更簡單的形式（降維）

3) 在簡化後的關係中使用簡單的方法（如K-Means）來分組

• ⚠️注意事項⚠️：
  • 計算量較大，需要進行特徵值分解，對計算資源要求較高
  • 需要選擇合適的相似度矩陣和簇數，比如要如何定義誰和誰更像朋友
  • 結果解釋可能不直觀：需要仔細思考分組的含義

結論

聚類演算法在無監督學習中能幫助我們自動識別數據中的隱含結構，並在客戶細分、圖像處理、基因分析等多個領域展現其強大的應用潛力。然而，這些方法在應用過程中也存在一些挑戰，如簇數的選擇、計算效率的考量，以及結果解釋的困難度等。

聚類算法在處理高維數據不僅增加了計算複雜度，還可能引入噪聲，影響聚類效果。因此，我們將在下一篇探討降維算法，這一技術不僅能夠減少數據的維度，降低計算負擔，還能幫助我們視覺化高維數據，進一步發現數據中的內在結構。

參考資料

https://blog.csdn.net/BryantDaiJB/article/details/120892597
https://taweihuang.hpd.io/2017/07/06/intro-spectral-clustering/