註：本文同步更新在Notion!（數學公式會比較好閱讀）

首先登場(・∀・)つ在踏入偉大航道需要的初始裝備「線性代數」！！！

線性代數是機器學習的基石，在模型中，其實是對數據進行一連串的線性轉換，而向量(vector)和矩陣(matrix)等是處理數據運算的招式。

包含了m個列向量或是n個行向量

矩陣的基本運算

我們派上矩陣$A$跟$B$來上演三個橋段吧！

• 劇本一 加法
  
• 劇本二 減法
  
• 劇本三 乘法
  

矩陣的轉置(Transpose)

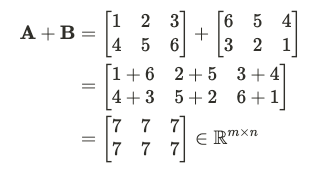
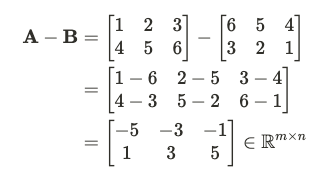
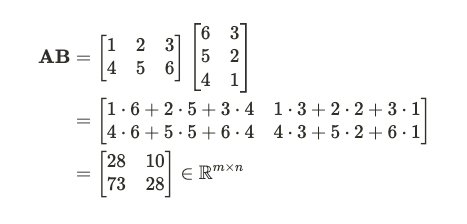
轉置就是將矩陣的行與列互換，形成一個新的矩陣A^T。
像是這樣：


後續的概念（如內積、行列式等）都涉及矩陣轉置唷～

矩陣的秩(Rank)

矩陣中線性獨立行向量或列向量的最大數目。秩反映了矩陣所能表示的線性獨立，舉例來說，矩陣是不是非退化性（滿秩矩陣）。

而對於方陣（即行數等於列數的矩陣），如果行列式不等於零，則矩陣是全秩的（即其秩等於矩陣的行數或列數）。

全秩矩陣：

• 對於 m×n 矩陣，如果它是全秩的，那麼它的行或列向量組成的子空間會是最大可能的維度。
• 對於方陣（即行數和列數相等）而言，全秩矩陣是可逆的。

明天會接續把線性代數寫完，感謝大家的閱讀，週末愉快(σ′▽‵)′▽‵)σ