註：本文同步更新在Notion!（數學公式會比較好閱讀）

感知機（Perceptron）

感知機是一種最基本的前饋式神經元模型，由 Frank Rosenblatt 在 1958 年提出。它是一個二類分類器，用來區分兩類樣本。
感知機接受輸入向量x = [x_1, x_2, ... , x_n] 並計算這些輸入的加權和，再通過一個激活函數來產生輸出。

感知機通過調整權重 w 和偏置 b 來學習將輸入數據映射到適當的分類結果。這個調整過程使用感知機算法來實現。

感知機模型

感知機是前饋式神經網路的最基本單元。其主要組成部分包括：

1. 輸入層（Input Layer）：接收輸入數據（特徵）
2. 權重（Weights）：每個輸入對應的權重
3. 偏置（Bias）：調整輸入和權重之和，使得模型更加靈活
4. 激活函數（Activation Function）：輸入總和通過激活函數轉換為輸出

感知機的輸出公式為：

感知機求解 AND 問題

AND 問題是一個簡單的線性可分問題，輸入是兩個二進制變量 x_1 和 x_2，輸出為這兩個變量的邏輯與運算結果。輸入和輸出如下：

要解決這個問題，我們設置一個兩個輸入的感知機，並通過學習更新其權重來實現分類。

步驟：

XOR 問題與感知機的局限性

XOR 問題是一個非線性可分問題。輸入是兩個二進制變量 x_1 和 x_2，輸出為它們的邏輯異或（XOR）結果。輸入和輸出如下：

為何感知機無法解決 XOR 問題？

XOR 問題是一個經典的非線性問題。兩類樣本（y=0 和 y=1）無法通過一條線性的決策邊界分開。因此，單層感知機無法解決這類問題。

解決方案：多層感知機（MLP）

為了處理非線性可分的問題，如 XOR，我們需要引入多層感知機（MLP），即具有一個或多個隱藏層的神經網絡。通過引入隱藏層，網絡可以學習到更複雜的非線性邊界，進而解決 XOR 問題。

一個 MLP 結構包括：

• 輸入層：兩個輸入節點 x_1 和 x_2。
• 隱藏層：隱藏層節點數量可以根據具體問題設置，對於 XOR 問題，兩個隱藏層節點即可解決問題。
• 輸出層：一個輸出節點，代表 XOR 結果。

步驟：

1. 輸入層到隱藏層的計算：
   
2. 隱藏層到輸出層的計算：
   
3. 訓練過程：通過反向傳播算法來更新權重，最小化損失函數（如均方誤差）。

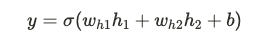
通過這種方式，多層感知機可以解決 XOR 問題，因為隱藏層提供了學習非線性邊界的能力。

感知機是前饋神經網絡的基礎，在解決線性可分問題（如 AND 問題）時非常強大。然而，對於像 XOR 這樣的非線性問題，單層感知機無法勝任，必須引入多層感知機（MLP）來處理這類問題。通過隱藏層，MLP 可以學習複雜的非線性映射。

⠀⠀ ((\⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀
( ⸝⸝◜ ° ꈊ ° ◝⸝⸝ )
づ🍛ど