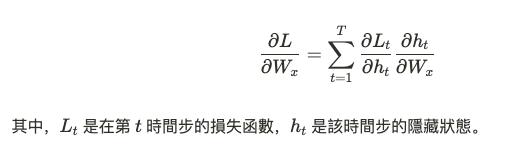註：本文同步更新在Notion!（數學公式會比較好閱讀）

遞迴式神經網路 (RNN) 的序列學習

在機器學習與深度學習的應用中，處理時間序列數據或順序依賴的數據（如自然語言處理、語音識別等）時，傳統的前饋式神經網路（FNN）不適用於捕捉序列中的時間關係。這時，遞迴式神經網路（Recurrent Neural Networks, RNN）便成為了強大的工具，能夠有效學習和處理序列資料。

1. RNN 的基本架構與序列學習

RNN 的核心特性在於其隱藏層的遞迴結構，能夠記住前一時間步驟的信息，並將其與當前的輸入結合進行運算。這種特性使 RNN 能夠自然而然地處理時間序列數據。具體來說，RNN 透過一個循環連結（recurrence）將上一時間步的隱藏層狀態傳遞給下一時間步，從而維持序列中的上下文信息。

序列學習的核心在於，RNN 通過時間步驟 ttt 的遞迴結構，不斷更新隱藏狀態，並保留之前的訊息，能夠有效捕捉長期依賴性。RNN 可用於多種序列到序列的問題，如語言翻譯（從一個句子生成另一個句子）。

2. 梯度消失與長期依賴問題

雖然 RNN 在序列學習上表現出色，但其在學習長期依賴性時存在梯度消失（vanishing gradient）問題。當序列很長時，RNN 的梯度在反向傳播時可能會變得極小，導致模型無法有效學習序列中的遠距離依賴。這是由於在多次時間步的矩陣乘法中，梯度逐漸縮小，最終無法有效更新參數。

為了解決這一問題，出現了幾種改進型 RNN 架構，如長短期記憶（LSTM）和門控循環單元（GRU）。這些變體通過引入門控機制來控制信息的流動，避免梯度消失問題，並能更好地學習長期依賴。

3. 序列學習的應用

RNN 和其變體廣泛應用於自然語言處理（NLP）中，如機器翻譯、語音識別、文本生成等。以語言翻譯為例，RNN 能夠處理一段話的語境，將前後文的信息考慮在內來生成合適的翻譯結果。在這樣的應用中，模型需要處理順序數據中的語意和上下文依賴性。

4.序列學習中的反向傳播

RNN 中的梯度更新使用反向傳播算法，但其特點是通過時間的反向傳播（Backpropagation Through Time, BPTT）。這個算法根據整個序列長度展開時間步，並依據序列的時間步展開損失函數，對每一步的參數進行更新。數學上，這涉及多次求導，具體形式如下：