註：本文同步更新在Notion!（數學公式會比較好閱讀）

在遞迴式神經網路（RNN）中，Elman 神經網路是其中的一個經典變種，由 Jeffrey Elman 於 1990 年提出。該模型通過引入上下文層（context layer）來改善 RNN 在序列學習中的性能，並且在語音識別、自然語言處理等任務中得到了廣泛應用。

1. Elman 神經網路的結構

Elman 神經網路是一個部分連接的遞迴式神經網路。它的關鍵特徵是引入了上下文單元來存儲之前時間步的隱藏層輸出，從而使模型能夠記住過去的信息，並在當前時間步中使用這些信息。

Elman 神經網路包括三個主要層次

2. Elman 網路的序列學習能力

Elman 神經網路的最大優勢在於其能夠有效處理序列資料，因為它的上下文層儲存了上一個時間步的信息，這使得模型能夠學習時間上的依賴關係。與標準的 RNN 不同，Elman 網路強調的是通過引入上下文層來更好地學習長期依賴性，並且能夠在每一個時間步中考慮當前和過去的信息。

從數學角度看，Elman 網路的優點在於其簡化的架構使得序列信息更容易反向傳播並更新權重，尤其是當序列依賴的時間跨度較短時，它能夠快速收斂。

3. Elman 網路的數學表示與訓練

在訓練過程中，Elman 神經網路仍然使用反向傳播算法，具體為通過時間的反向傳播（Backpropagation Through Time, BPTT）。與標準 RNN 一樣，BPTT 將誤差根據時間步展開，並反向傳播到每一個時間步進行參數更新。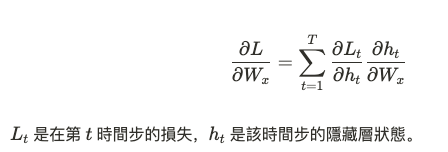

4. Elman 網路的應用與局限性

Elman 神經網路在一些序列學習問題上，如詞性標註、語言建模、語音識別等應用中得到了成功。然而，它也存在一定的局限性，主要是當處理長序列依賴時，Elman 網路仍然容易受到梯度消失問題的影響。

因此，儘管 Elman 神經網路在一些應用上效果不錯，但它的表現往往會在序列長度增加時下降。這為後來的**長短期記憶（LSTM）和門控循環單元（GRU）**的發展鋪平了道路，這些模型能夠更好地處理長期依賴問題。

5. Elman 網路的數學意涵

Elman 網路的架構簡化了隱藏層狀態的更新公式，使得模型的運算效率更高。在數學上，這種通過上下文層儲存過去隱藏狀態的設計相當於將序列信息以加權和的形式融入到當前步驟的計算中。這樣的架構在一定程度上平衡了模型的記憶能力和計算效率，使其能夠在較短序列的學習中表現出色。

提醒各位明天要上班QQ～