我們今天要來探討的是Deep Learning的架構設計，今天我們會通過學習CNN學到Network的架構要如何設計，以及基於什麽樣的考量來做出這樣的設計。

CNN一開始是專門用在影像上的一個Model，假設我們今天要給一張圖片分類，機器需要判斷圖片裏面的是什麽動物。在做CNN的時候，我們的輸入是一張圖片，而通常我們的圖片大小需要是固定的，比如100*100的解析度，如果今天有不同大小不同比例的圖片出現，我們可能會需要將它rescale成同樣的大小。

那麽我們的輸出是什麽呢？因爲是一個分類的問題，所以我們的輸出應該會是一個one hot vector。這個one hot vector是什麽呢？簡單來説，就是正確的類別是1，其他類別都是0的vector，至於要有多少的dimensions，則是看你的模型可以變是多少種類，假設你的model只能辨識貓，狗，人，鴨子，那麽你的dimension就是4。

當我們輸入一張圖片給model，我們的model輸出通過softmax激活函數以後，會拉開最大值和其他值的差距，這時候我們的輸出y'是一個vector，我們希望輸出y'和labely hat之間，他們的cross-entropy越小越好。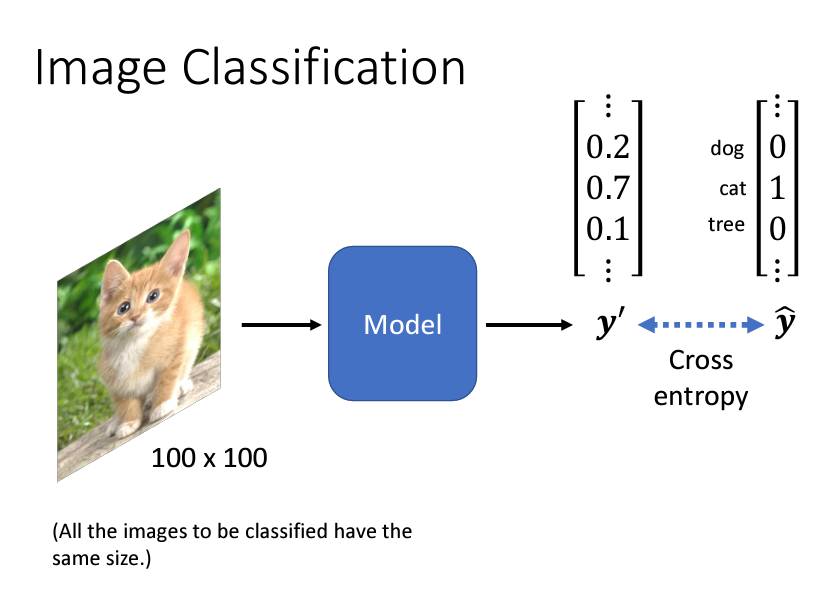

模型的輸入

我們説CNN的輸入會是一張圖片，那麽對於機器來説，這張圖片需要怎麽樣的處理才可以被我們拿來做運算呢？我們回想一下之前在做linear regression或是logistics regression的時候，我們的輸入是什麽？是一個vector對吧！我們會對我們的問題去做特徵工程，最後我們有多少個feature，我們的input vector就有多少個dimension。

我們之前的做法用在CNN也同樣如此，我們現在需要理解一張圖片在機器，在電腦裏是什麽樣子的。假設我們的照片大小是100*100,一張圖片是一個二維的matrix，但是如果是一張彩色的圖片的話，我們有r，g，b三個管道，就是100*100*3的一個3d tensor（張量），那麽這個3d的 tensor我們需要做的就是對它的每個顔色都拉直變成vector，然後把這三個顔色的vector接在一起形成一個巨大的vector，這裏的每一個數值都表示說在那個顔色的强弱：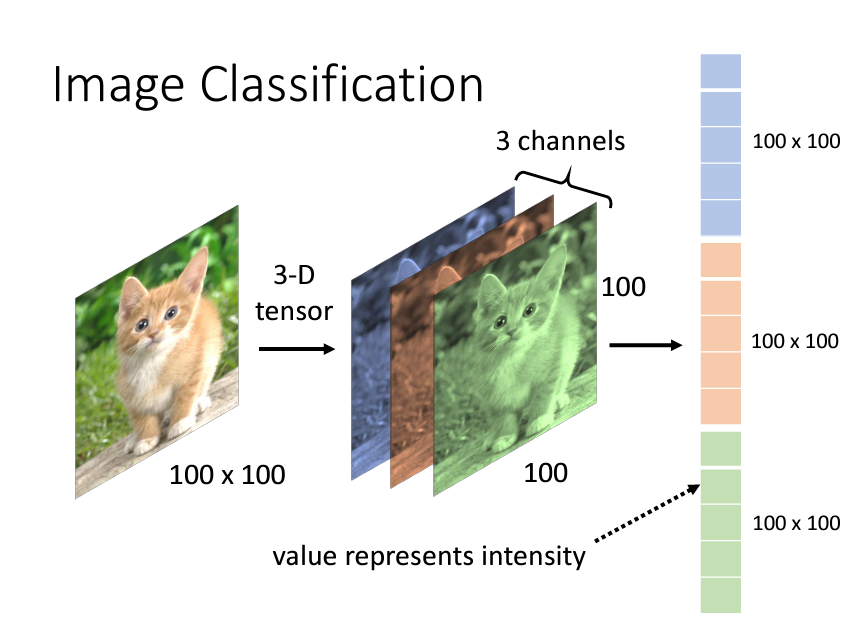

如果說今天考慮我們的model裏面會與多少個參數，假設我們是一個fully connect的network，裏面的layer1有一千個neuron，那麽我們的每個x_i都對每個neuron都有一個w_i，那麽我們總共會有100*100*3*1000個w這麽多的參數。

我們之前有説過w和b對應的關係，所以我們知道說今天如果是一個很簡單的model，它的feature很少的話，那麽這樣太過於簡單的一個model，他的bias可能會比較大；而如果今天參數很多的話，會造成我們的variance較大，進而可能導致我們的model overfitting的可能性也變大，所以我們現在會遇到的一個問題，那就是我們真的需要這麽大的參數量嗎？我們真的需要一個fully connected的network嗎？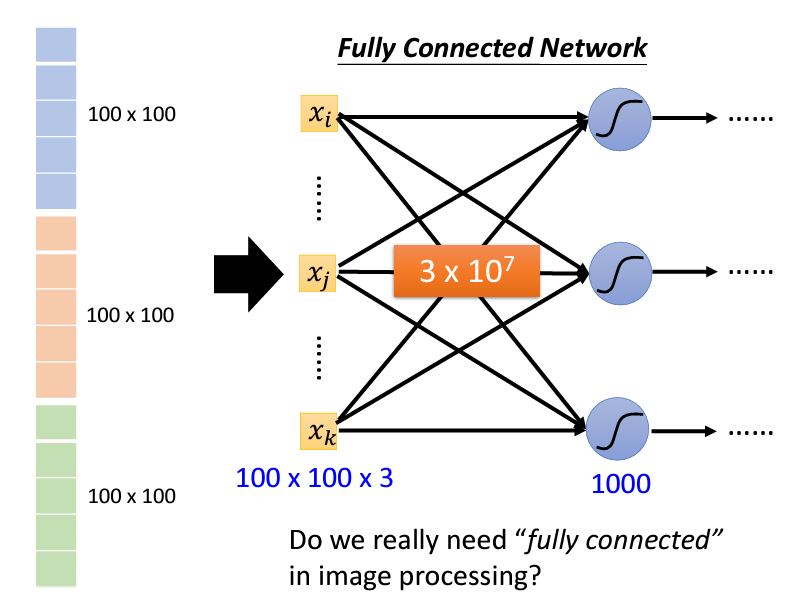

爲了解決問題，我們需要重新來檢視一下我們要解的任務的性質。

觀察1

當我們人類在辨識一張圖片的時候，我們是怎麽認出圖片裏的是貓、狗還是鳥呢？我想應該都是通過一些特徵來辨認的，比如説有喙、有爪子的脚、眼睛很小，我們就認爲這是一隻鳥：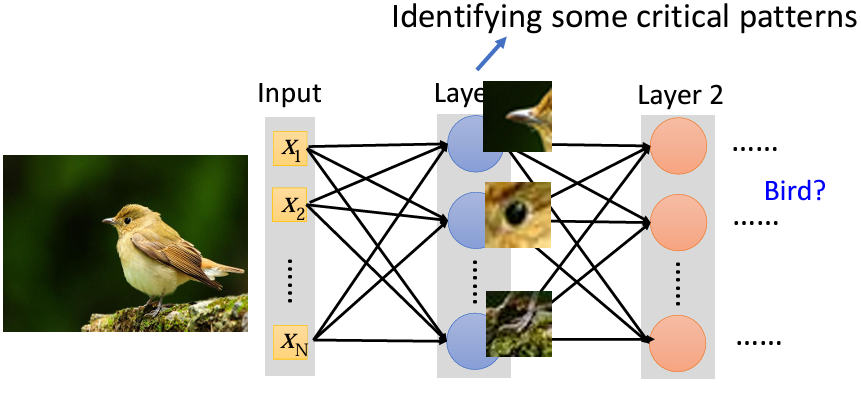

那麽既然我們要辨識出圖片裏是什麽動物只需要圖片部分的像素，有沒有辦法讓每個neuron只看部分的像素而不是整張圖片呢？那樣的話我們的參數就可以瞬間少很多。

其實是由一個辦法的，那個辦法就是守備範圍Receptive field，我們原本100*100*3的像素對每個neuron都有一個自己的weight，那麽我們今天劃出很多個Receptive field，然後每個Receptive field都有對應的neuron來負責守備，那樣的話就會變成：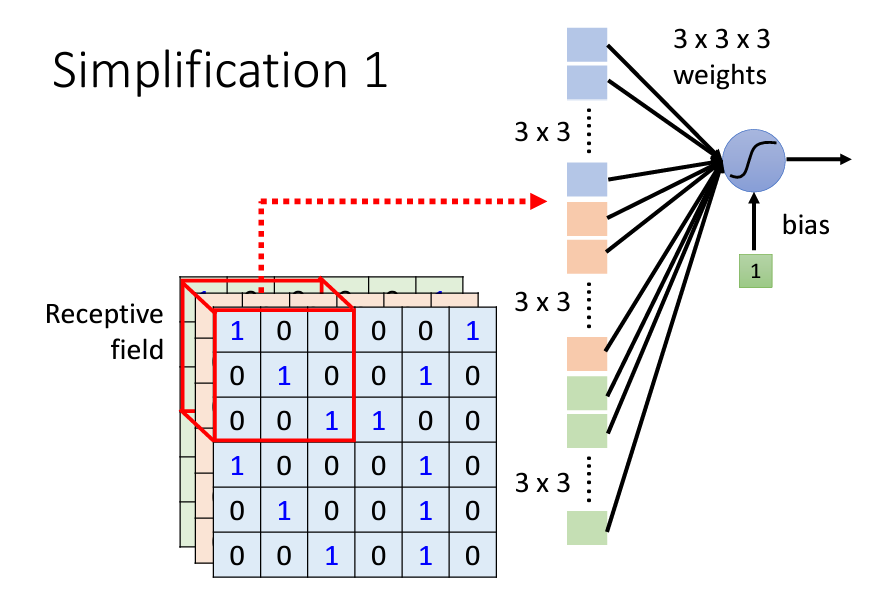

這個Receptive field有幾個特性：

• 一個Receptive field通常由多個neuron來負責守備
• Receptive field和Receptive field之間可以重叠，并且全部的Receptive field會覆蓋整張圖片
• Receptive field和Receptive field重叠的間隔叫做stride
• 如果Receptive field超出圖像的範圍，那麽會對圖像進行padding（可以是補0、將邊緣的位置重複補上……）
• 最常見的Receptive field的安排方式會看所有的channel，所以往往會忽略掉channel，而只看二維的matrix，稱爲kernel size。

觀察2

可能同一個特徵會在圖片的不同位置出現，導致了每個Receptive field都會有同樣的neuron偵測同樣的特徵：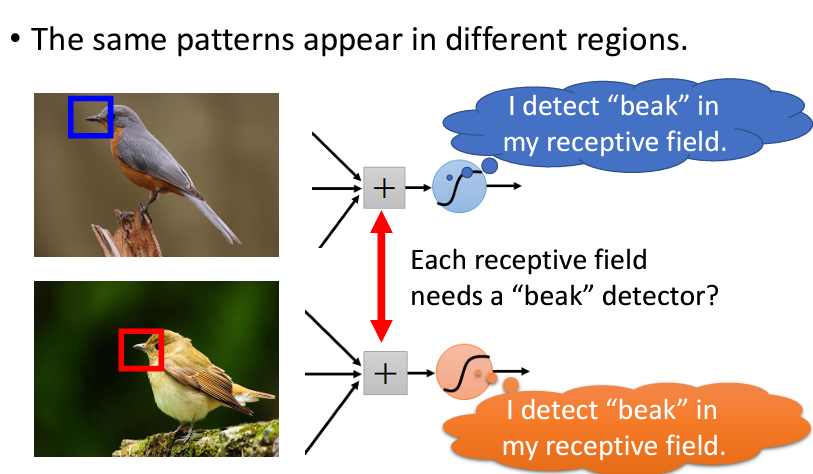

還記得我們做這些觀察的初衷嗎？我們是爲了減少我們的參數所以針對圖像做了這些觀察，但是現在發現很多的neuron都在做重複的事，因此我們需要想辦法讓這些neuron能夠共用，所以要怎麽做呢？我們可以通過讓這些做同樣的事的neuron共享參數：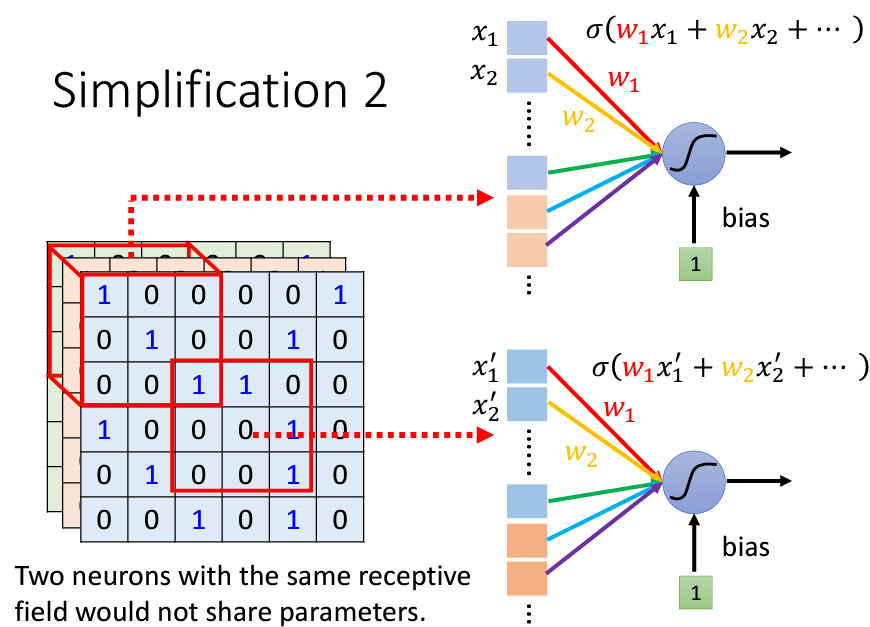

雖然參數（weight）是共享的，但是因爲輸入的值不一樣（每個守備範圍的vector都不一樣），因此不會得到相同的輸出。

因此我們可以知道常見的做法就是，給每個Receptive field設置一組neuron（如64個），每個Receptive field用的neuron其實都是同一組，因爲它們之間的參數是共享的，每一個neuron就是在識別一個feature，我們可以把這個neuron叫做一個filter，所以有64個neuron就可以說是有64個filter。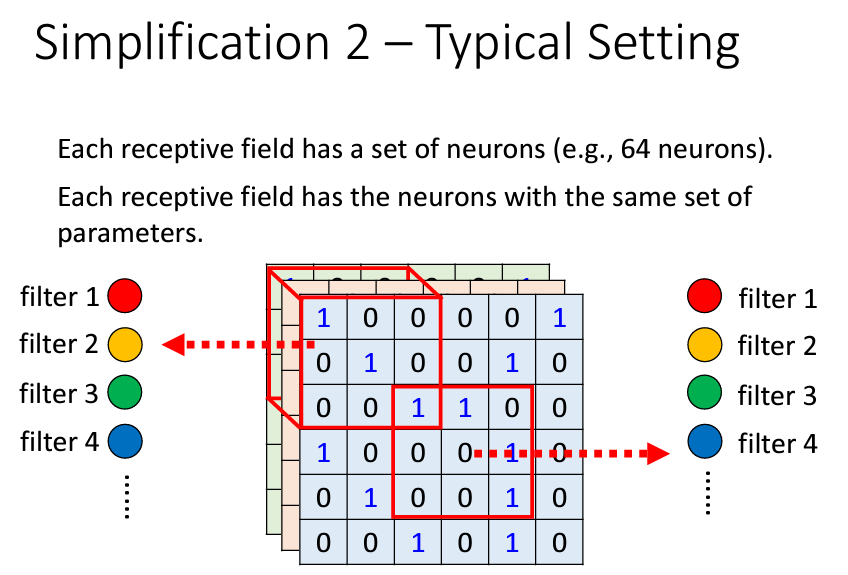

在經過這兩個觀察后，我們可以得到的結論是對於影像辨識這件事，我們並不需要一個fully connected的network，只需要針對整張圖片設定多個Receptive field，并且讓每個Receptive field的參數是共享的，當我們做了這兩件事后，我們就可以把這層layer稱作卷積層（Convolutional Layer）。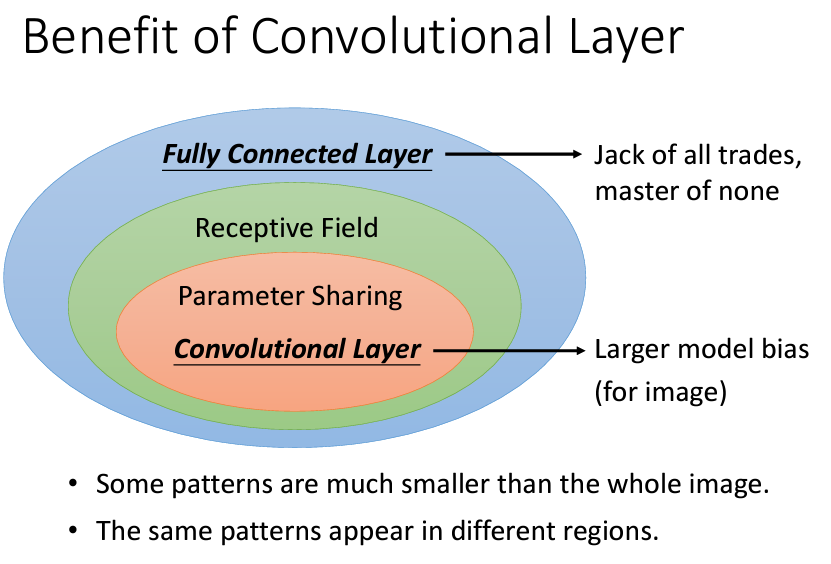

至於還有另外一種角度來切入卷積層這個主題，做法是一模一樣的，這邊就不多説了，感興趣的話可以看

觀察3

我們發現其實一張圖片，在遺失了一些信息後，依然不會改變這張圖片的内容，比如説我們可以把橫軸奇數的像素點移除，縱軸的偶數點移除，整張圖片的内容依舊不影響我們的判斷：

基於這個觀察，我們可以對圖片進行一個叫做池化（Pooling）的操作，比如説我們將經過卷積層過後的圖像以2*2為一組，選出這四個裏面最大的值，這就叫max pooling，如果是將四個點進行加總取平均，就叫做mean pooling。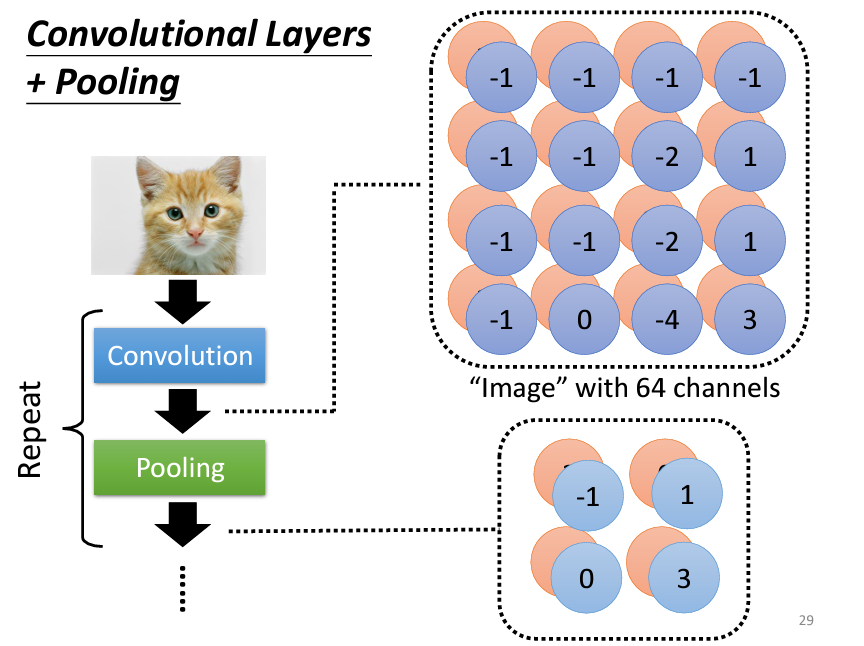

接下來我們就可以反反復復進行下去，然後最終把處理過後的圖像進行扁平化處理（也就是攤平變成vector），再將它輸入到全連接層，最終在輸出層通過softmax激活函數，就可以得到一個vector，這個vector裏面的每一個y_i都是對應的class的機率，比如説[0.11, 0.88, 0.01]，那麽顯然0.88是最有可能的，他就屬於該類別。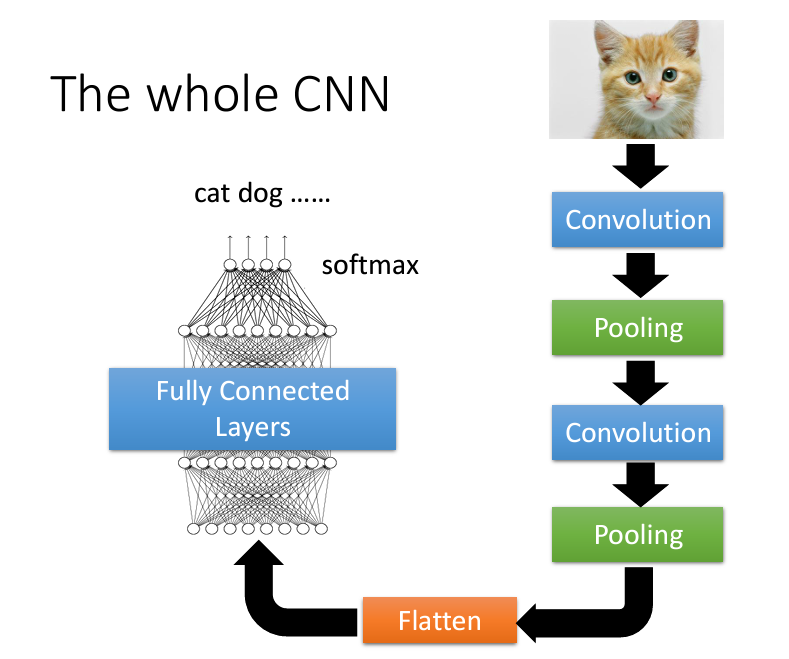

要記得，CNN一開始是設計用在影像上的，如果要應用在其他的地方，應該根據該領域的特性去重新設計，否則的話可能會得到一個很爛的performance。

以上的内容來自於臺大教授李宏毅：鏈接，我只是把他的影片寫成了筆記。