本文同步刊載於 「為你自己學 Python - 類別繼承與家族紛爭（中））」

類別繼承與家族紛爭（中）

這個章節我們先稍微喘口氣，暫時不看 CPython 的原始碼，先來看看 Python 的多重繼承是怎麼計算方法的查找順序，或是如果遇到上層多個類別都有實作同一個方法的時候，該聽誰的。

C3 線性演算法

關於 Python 採用 C3 線性演算法，我借用維基百科的一段話：

Python 創始人 Guido van Rossum 這樣總結C3超類線性化：「基本上，在 C3 背後的想法是，如果你寫下在複雜的類層級中繼承關系所施加的所有次序規則，這個演算法將確定出滿足所有這些規則的這些類的一個單調次序。如果不能確定出這樣的次序，這個演算法會失敗。」

這裡的重點在於「單調次序（Monotonicity）」，也就是說不管在簡單或複雜的繼承關係裡，C3 線性演算法都會試著計算並找出一個合理的次序，如果能計算的出來，那將會每次都是一樣的結果。

該聽誰的？

我們先來看一段程式碼：

class A:
    def greeting(self):
        print("Hey in A")

class B(A):
    def greeting(self):
        print("Hey in B")

class C(A):
    def greeting(self):
        print("Hey in C")

class D(B, C):
    pass

d = D()
d.greeting()

這是個還算單純的多重繼承結構，類別 D 同時有兩個上層類別，那麼當呼叫 d.greeting() 的時候，該聽誰的？這個狀況比較簡單，因為類別 D 的上一層就是類別 B，而類別 B 有自己的 greeting 方法，所以會呼叫類別 B 的 greeting 方法。嗯...但為什麼是 B 而不是 C，這兩個不是同一層嗎？

我讓故事變的複雜一點點，如果類別 B 沒有定義 greeting() 方法呢？像這樣：

class A:
    def greeting(self):
        print("Hey in A")

class B(A): pass

class C(A):
    def greeting(self):
        print("Hey in C")

class D(B, C): pass

如果類別 B 沒有定義 greeting() 方法，那麼接下來是會往上找類別 A，還是往旁邊找同一層的類別 C 呢？在 Python 決定查找順序的設計叫做 MRO，全名是 Method Resolution Order，我們可以透過類別的 .mro() 方法來查看：

>>> D.mro()
[<class '__main__.D'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.A'>, <class 'object'>]

順序是 D -> B -> C -> A，最後是每個類別的大家長 object，所以如果呼叫 d.greeting() 的時候，在類別 B 沒有定義方法的情況，會往下一個順序，也就是類別 C 的 greeting 方法。

Python 的 MRO 是採用「C3 線性演算法（C3 Linearization Algorithm）」，這個演算法在 Python 2.3 之後開始被採用。這個演算法的目的是要找出一個合理的繼承順序，讓每個類別的方法都能被正確的呼叫到。

那麼在 2.3 之前呢？在這之前，Python 使用的是「深度優先搜尋（Depth-First Search）」的方式來找出 MRO，以剛才的範例算出來會是 D -> B -> A -> C，這樣的順序在某些情況下會導致問題，例如傳說中的「菱形繼承（Diamond Inheritance）」問題。

MRO 計算

單一繼承

我們先從最簡單的單一繼承開始，為了簡化，我暫時先讓類別裡就先放個 pass 不做事：

class A: pass
class B(A): pass

現在的繼承圖大概像這樣：

在計算 A 的 MRO 之前，雖然 A 類別沒有明顯的繼承其他類別，但在 Python 3 會自動幫我們繼承 object 類別，所以現在繼承關係是這樣：

先從最上層的 object 開始算，接下來我會用 L<類別> 來表示類別的線性化順序（Linearization Order），也就是 MRO：

L<object> = [object]

因為 object 是最上層了，所以只有一個元素 [object]。接下來是類別 A：

L<A> = [A] + merge(L<object>, [object])

這公式看起來一開始看的時候有點複雜，其實就是這個類別加上它的這些上層類別的線性化順序，以及這些上層類別的列表的唯一合併的總和。

合併的計算方法，是選擇這些列表的頭部（Head）中第一個符合條件的，如果符合條件，稱之「良好頭部（Good Head）」，但我個人比較喜歡叫它「好線頭」，因為就像是在整理一堆線的時候，要找一條好的線頭開始整理。

要當一個好線頭的條件，就是這個元素在其它的列表不再出現，或是就算出現也是出現在列表的頭部。我們直接來進行計算可能會更清楚一點。在上面的公式中，首先要先把 L<object> 展開，所以原來的公式就會變成：

L<A> = [A] + merge([object], [object])

然後開始找頭，不過因為這裡只有一個 object，所以就直接把它從列表裡抽出來，L(A) 經過合併計算後：

L<A> = [A, object]

這個有點太簡單感受不太出來計算的過程，接下來我們再來看看 B 類別：

L<B> = [B] + merge(L<A>, [A])

這個合併就要稍微算一下了，首先，我把前面算過的 L<A>先展開，變成：

L<B> = [B] + merge([A, object], [A])

再來，merge 的過程要從後面這幾個列表裡抽出一個好的線頭（Good Head），先從第一個 A 開始。我剛好用這個例子，再把當一個好線頭的遊戲規則整理如下：

1. 如果 A 沒有出現在後續的其它列表，或是有出現，而且也是第一個，那就是個好的線頭，跳到步驟 3。
2. 承步驟 1，如果 A 不是合適的線頭，找下一個列表的頭，然後回到步驟 1。
3. 把 A 從所有列表裡抽出來往前擺，然後回到步驟 1，繼續找下一個元素。

在這裡例子裡，A 有出現在最後一個列表裡而且是第一個，所以它是個好線頭，把 A 從所有列表裡抽出來，現在變成：

L<B> = [B, A] + merge([object])

再來的合併就簡單了，因為 object 在所有列表裡都是第一個（也就剩它一個），最後的結果是：

L<B> = [B, A, object]

執行類別的 .mro() 方法來驗算一下：

>>> A.mro()
[<class '__main__.A'>, <class 'object'>]
>>> B.mro()
[<class '__main__.B'>, <class '__main__.A'>, <class 'object'>]

看起來沒問題。這是單一繼承的情況，再來我們來看看多重繼承的情況。

多重繼承

先來個單純一點的多重繼承：

class A: pass
class B(A): pass
class C(A): pass
class D(B, C): pass

現在的繼承結構大概像這樣：

這裡的 L<A> 跟上面的例子一樣，而 L<B> 與 L<C> 分開看的話，其實它們兩個對類別 A 來說是單一繼承，所以算出來的答案跟前面單一繼承的答案差不多，分別是：

L<B> = [B, A, object]
L<C> = [C, A, object]

重點是最下層的 L<D>：

L<D> = [D] + merge(L<B>, L<C>, [B, C])

把 L<B> 跟 L<C> 展開，準備進行合併：

L<D> = [D] + merge([B, A, object], [C, A, object], [B, C])

開始找好線頭，先從 B 開始，B 有出現在最後一個列表裡而且是第一個，所以是好線頭，把 B 從所有列表裡抽出來：

L<D> = [D, B] + merge([A, object], [C, A, object], [C])

繼續找下一個線頭，下一個是 A，A 有出現在第二個列表 [C, A, object]，但它不是第一個，所以不是個好線頭。沒關係，換下一個列表的頭 C 來試試看。嗯，C 有出現在最後一個列表裡而且是第一個，所以是好線頭，把 C 從所有列表裡抽出來：

L<D> = [D, B, C] + merge([A, object], [A, object], [A, object])

繼續找下一個線頭 A，A 有出現在所有列表裡而且是第一個，所以是好線頭，把 A 從所有列表裡抽出來：

L<D> = [D, B, C, A] + merge([object], [object], [object])

最後收尾，把 object 從所有列表裡抽出來：

L<D> = [D, B, C, A, object]

來驗算一下：

>>> D.mro()
[<class '__main__.D'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.A'>, <class 'object'>]

結果跟我們手算的是一樣的。

以結果來說，看起來流程是是先往上層找，接著往平行層找，平行層都找完之後再繼續往上層找，直到最後的上層類別 object 為止。但這是比較單純一點的例子，我們來看個稍微複雜一點的例子...

複雜一點的繼承

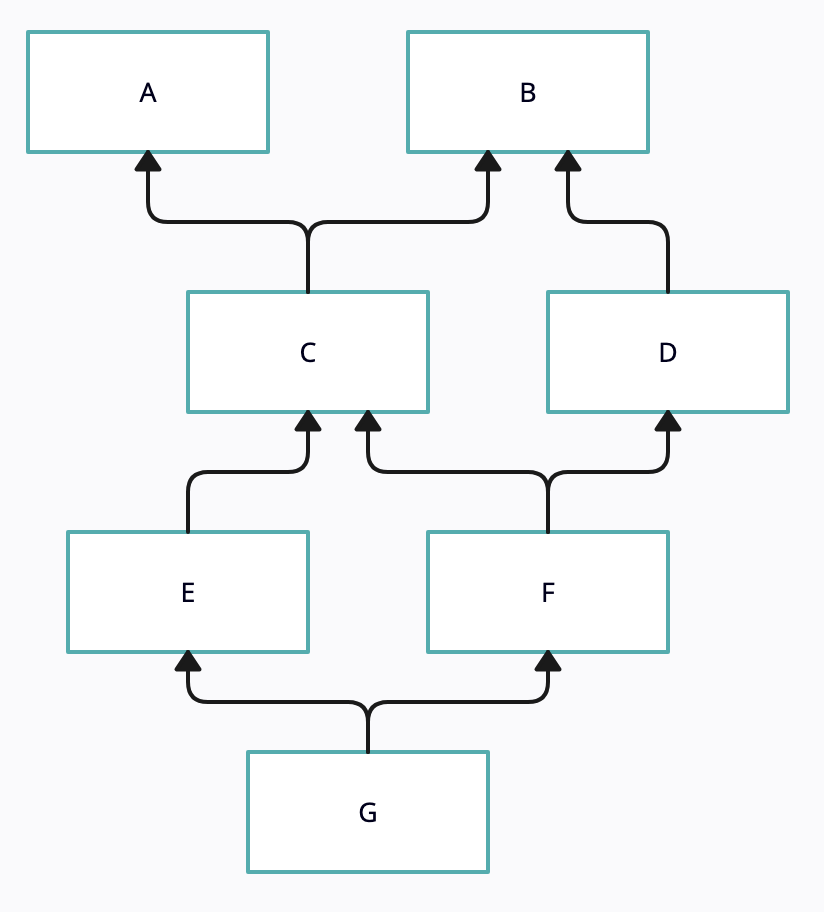
先上程式碼：

class A: pass
class B: pass
class C(A, B): pass
class D(B): pass
class E(C): pass
class F(D, C): pass
class G(F, E): pass

這看起來好像不只複雜一點點：

沒關係，我們一樣從最簡單的開始：

L<A> = [A, object]
L<B> = [B, object]
L<C> = [C, A, B, object]

然後 L<D> 是單一繼承，所以也不難算：

L<D> = [D, B, object]

再來是 L<E>：

L<E> = [E] + merge(L<C>, [E])

先展開 L<C>：

L<E> = [E] + merge([C, A, B, object], [C])

開始合併，C 是好線頭，抽出來：

L<E> = [E, C] + merge([A, B, object])

後面剩一個列表就沒什麼好抽了，直接合併：

L<E> = [E, C, A, B, object]

再來算 L<F>：

L<F> = [F] + merge(L<D>, L<C>, [D, C])

展開 L<D> 跟 L<C>：

L<F> = [F] + merge([D, B, object], [C, A, B, object], [D, C])

開始合併，D 是個好線頭，抽出來：

L<F> = [F, D] + merge([B, object], [C, A, B, object], [C])

接著，B 有在後面的列表出現，但不是頭部的位置，不是好線頭。換下一個列表的 C，它符合好線頭的條件，抽出來：

L<F> = [F, D, C] + merge([B, object], [A, B, object])

再試一次 B，但很可惜現在它一樣不是好線頭，所以只好選擇下一個列表的 A，它是好線頭，抽出來：

L<F> = [F, D, C, A] + merge([B, object], [B, object])

剩下的都一樣，可直接合併，最後得到：

L<F> = [F, D, C, A, B, object]

最後一個 L<G>：

L<G> = [G] + merge(L<F>, L<E>, [F, E])

展開 L<F> 跟 L<E>：

L<G> = [G] + merge([F, D, C, A, B, object], [E, C, A, B, object], [F, E])

為了節省篇幅，這裡稍微快轉一下：

L<G> = [G] + merge([F, D, C, A, B, object], [E, C, A, B, object], [F, E])
L<G> = [G, F] + merge([D, C, A, B, object], [E, C, A, B, object], [E])
L<G> = [G, F, D] + merge([C, A, B, object], [E, C, A, B, object], [E])
L<G> = [G, F, D, E] + merge([C, A, B, object], [C, A, B, object])
L<G> = [G, F, D, E, C, A, B, object]

基本上也是照著先往上層找，再往平行層找，然後再繼續往上層找的順序。驗
驗算一下 F 跟 G：

>>> F.mro()
[<class '__main__.F'>, <class '__main__.D'>, <class '__main__.C'>, <class '__main__.A'>, <class '__main__.B'>, <class 'object'>]
>>> G.mro()
[<class '__main__.G'>, <class '__main__.F'>, <class '__main__.D'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.A'>, <class '__main__.B'>, <class 'object'>]

看起來沒錯。

其實整個計算的過程只是看起來複雜，但流程都是一樣的。透過 C3 線性演算法，Python 可以確保在多重繼承的情況下，繼承順序是有序而且每次都是唯一的。

算不出來？

再來個例子：

class A: pass
class B(A): pass
class C(A): pass
class D(B, C): pass
class E(C, D): pass

現在的繼承圖大概長這樣：

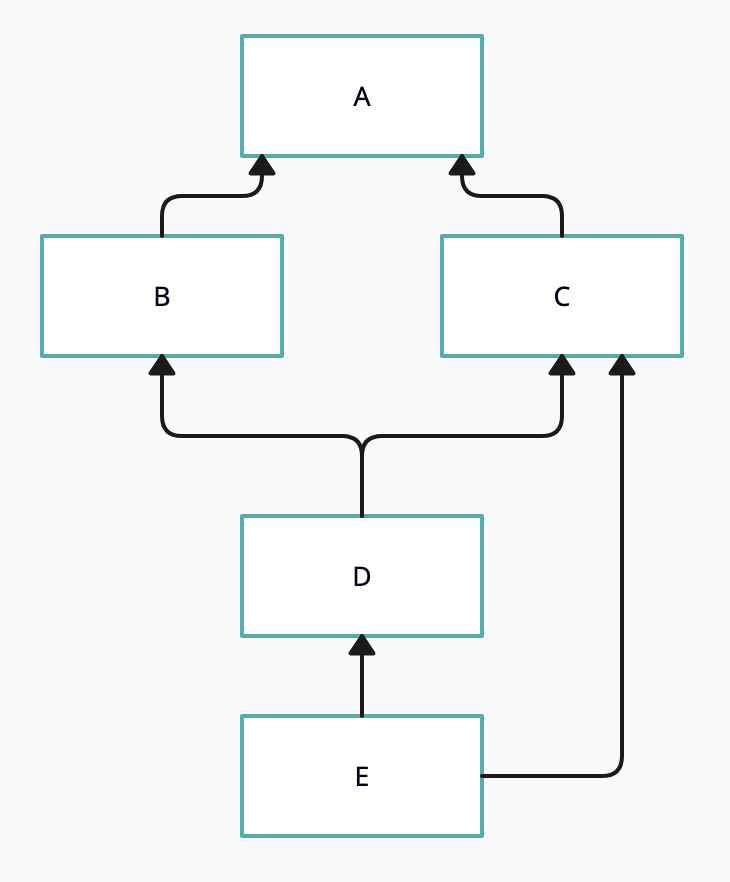
L<A> = [A, object]
L<B> = [B, A, object]
L<C> = [C, A, object]

再來是 L<D>：

L<D> = [D] + merge(L<B>, L<C>, [B, C])

展開 L<B> 跟 L<C>：

L<D> = [D] + merge([B, A, object], [C, A, object], [B, C])

開始合併，快轉一下：

L<D> = [D] + merge([B, A, object], [C, A, object], [B, C])
L<D> = [D, B] + merge([A, object], [C, A, object], [C])
L<D> = [D, B, C] + merge([A, object], [A, object])
L<D> = [D, B, C, A, object]

最後一個 L<E>：

L<E> = [E] + merge(L<C>, L<D>, [C, D])

展開 L<C> 跟 L<D>：

L<E> = [E] + merge([C, A, object], [D, B, C, A, object], [C, D])

開始合併，先從 C 開始，嗯，它不是好線頭，換下一個 D，嗯...它也不是，再換下一個又是 C，啊，沒了，沒有任何一個好線頭，也就是這樣的繼承關係無法滿足 C3 線性化的合併條件。這時候 Python 會拋出一個 TypeError 的例外：

TypeError: Cannot create a consistent method resolution
order (MRO) for bases C, D

「不是每個戀曲都有美好回憶♫♪」

並不是所有的多重繼承都能夠成功算出 MRO，這時候就要考慮一下是不是真的需要這麼複雜的繼承關係，或是可以透過改變繼承順序來解決這個問題。

下一集，我們繼續來看看 C3 演算法在 CPython 裡是怎麼實作的。

本文同步刊載於 「為你自己學 Python - 類別繼承與家族紛爭（中））」