Lattice 不是橫空而出，而是經過很多專家的研究，一步一步發展出來的，在深入理解 Lattice 之前，可以先了解相關的早期研究，相信會有助大家更深入地認識它。

Ajtai’s Function and Ajtai-Dwork Encryption
在一項開創性工作中，Ajtai [Ajt96] 首次給出了格(Lattice)問題的最壞情況到平均情況的歸約，並由此獲得了第一個基於格問題的密碼對象，其安全性證明依賴於格上經過充分研究的計算問題的難解性。特別是，Ajtai 的工作首次給出了基於標準最壞情況複雜性假設的密碼函數。Ajtai 引入了（平均情況下的）"短整數解（SIS）"問題及其關聯的單向函數，並證明解決它至少與在最壞情況下近似各種格問題一樣困難。SIS 和 Ajtai 的函數至今仍在密碼應用中廣泛使用。
在 1997 年的後續工作中，Ajtai 和 Dwork [AD97] 給出了一種基於格的公鑰加密方案，可以參看[AD07]。由於所有基於格的加密方案都繼承了該系統的基本模板。在高層次上，阿傑塔和德沃克給出了兩個主要結果：首先，他們證明 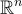中某個平均情況下的"隱藏超平面問題（HHP）"至少與任意 n 維格上的"γ-唯一最短向量問題 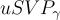"一樣困難，其中 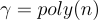是維度 n 的多項式。其次，他們構造了一個公鑰密碼系統，其語義安全性可以基於隱藏超平面問題的難解性，從而基於 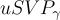的假設最壞情況難解性來證明。
作為第一個在最壞情況複雜性假設下具有安全性證明的加密方案，Ajtai-Dwork 的方案是一項理論突破。然而，從實際（甚至理論）角度看，它有一些顯著的缺點：其公鑰大小為 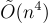，私鑰和密文大小為 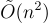，加密和解密的運行時間也相應匹配。為了抵抗針對隱藏超平面問題的密碼分析攻擊 [NS98]（從而防止密鑰恢復攻擊），n 的值必須在數百量級，這導致公鑰大小達到數千兆bits。此外，每個密文僅加密一個bit，因此要加一個 128 bit 的對稱密鑰需要密文大小達到 mega bit。後續工作在很大程度上解決了這些缺點。

隱藏超平面與唯一-SVP
非正式地，Ajtai 和 Dwork 引入的隱藏超平面問題如下：設 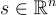是一個秘密的隨機短向量。目標是在給定許多點 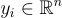的情況下找到 s，這些點滿足 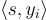接近整數，即 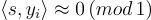。換句話說，每個 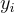接近平行的(n-1)的
維度的超平面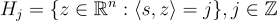 
中的一個。注意這是一個平均情況問題，因為秘密 s 和點 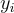是從某些規定的分佈中隨機選擇的。
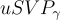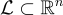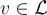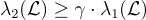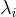唯一最短向量問題 定義如下：設 是任何具有"γ-唯一"最短向量的格，這意味著最短非零向量 的長度至少比所有不平行於 v 的格向量的長度小 γ 倍。更簡潔地說： ，其中 表示格的第 i 個逐次最小值。 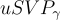的目標是在給定 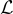的任意基的情況下，找到 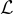中的最短非零向量。注意 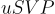是一個承諾問題，因為輸入格 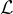必須滿足 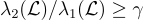。（或者，如果它不滿足承諾，則任何答案都被認為是正確的。）它也是一個最壞情況問題，因為沒有對格 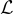或其基的分佈；聲稱解決 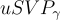的算法必須對任何滿足承諾的 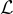都有效。

密碼系統與安全性
簡而言之，Ajtai-Dwork 密碼系統的工作原理如下：公鑰和私鑰分別是隱藏超平面問題的隨機實例 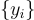及其解 s。要加密一個bit，生成一個密文，該密文要麼是 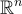中的"隨機"點（加密 0），要麼是公鑰中給出的點 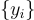的隨機子集的和（加密 1）。生成的點 y 分別要麼"遠離"所有隱藏超平面 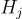，要麼"接近"其中一個。接收者可以使用其私鑰 s 區分這兩種情況（從而解密），只需測試 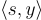是否接近整數。
作為其安全性證明的一部分，Ajtai 和 Dwork 給出了一個搜索到決策的歸約，表明任何能夠以任何顯著優勢區分上述兩種情況的竊聽者，都可以被高效轉化為一個以接近 1 的概率解決 HHP 的算法。換句話說，破解密碼系統的語義安全性至少與解決 HHP 一樣困難。其證明的第二部分表明，任何解決 HHP 的算法都可以轉化為一個在最壞情況下解決 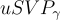的算法，其中 。

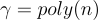NTRU
在 1996 年與 Ajtai 的工作同時（但直到 1998 年初才發表）， Hoffstein, Pipher, and
Silverman [HPS98] 設計了公鑰加密方案 NTRU (NTRUEncrypt)。這是第一個使用多項式環的密碼構造，這可以最有效地解釋為代數結構化的格。NTRU 密碼系統實際高效且具有相當緊湊的密鑰，並且在適當參數化時能夠抵抗重大的密碼分析努力。（不過要注意，早期的參數化有點過於緊湊，並且被證明具有不足的具體安全性，針對這部分可以參看[CS97]。）與 Ajtai-Dwork 及其同類方案不同，對 NTRU 密碼系統及其相關的平均情況計算問題的理論理解相對較少。特別是，沒有已知的從任何最壞情況下格問題到 NTRU 問題的任何標準版本的歸約，也沒有從 NTRU 問題到破解密碼系統語義安全性的歸約。（然而，NTRU 密碼系統的一個變體已被證明是安全的 [SS11]，假設環-LWE 的難解性）
NTRU 密碼系統由某個多項式環 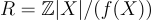參數化，例如對於素數 n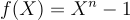， ，或對於 n 是 2 的冪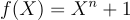， ，以及一個足夠大的奇數模數 q，定義商環 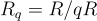。簡而言之，公鑰是 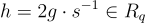，其中 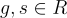是兩個"短"多項式（即具有相對較小的整數係數），其中私鑰 s 還被選擇為在模 q 和模 2 下可逆。加密基本上涉及將 h 乘以一個短"盲化"因子 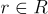，並添加一個短誤差項 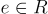，該誤差項將其係數模 2 中的消息 bit 編碼，得到密文 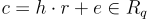。解密是通過將密文乘以私鑰得到 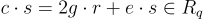，並將結果解釋為 R 中的短元素，這之所以有效是因為 g,r,e 和 s 都很短。由此恢復 e⋅s 模 2，從而恢復 e 模 2，以恢復消息的bit。（這個基本模板有一些稍微更高效的變體，例如選擇 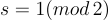，使得 。）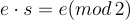
可以定義許多與 NTRU 相關的搜索和決策問題，例如給定公鑰找到私鑰、區分公鑰與均勻隨機、以及破解方案的語義安全性。

戈德賴希-戈德瓦瑟 Goldreich-Goldwasser-Halevi -哈萊維加密與簽名
受到 Ajtai 開創性工作 [Ajt96] 以及 McEliece 基於代碼的密碼系統 [McE78] 的啟發，Goldreich, Goldwasser, and Halevi（GGH）[GGH97] 提出了一種基於格問題的公鑰加密方案和數字簽名方案。與 Ajtai 和Ajtai-Dwork [AD97] 的工作不同，GGH 的提案沒有提供任何最壞情況下的安全性保證；它們的假設安全性僅僅是啟發式的。事實上，GGH 加密方案在實際參數大小下被成功密碼分析（但沒有在漸進意義上被破解）[Ngu99]，而 GGH 簽名方案後來被完全破解 [NR06]。然而，GGH 提案的核心思想後來以允許在最壞情況下硬度假設下進行安全性證明的方式被復活和實例化，並隨後導致了各種應用的巨大發展。
GGH 加密和簽名背後的主要思想是，公鑰是某個格的"壞"基，而對應的私鑰是同一格的"好"基。粗略地說，"壞"基由長且高度非正交的格向量組成，而"好"基由相對較短的格向量組成。這樣的基可以一起生成，例如首先選擇好基，然後將其乘以某個隨機選擇的么模變換（保持格不變）以獲得壞基。 或者，每個整數格都有一個特殊的基，稱為埃爾米特正規形，在某種意義上是格的"最難"基，因為它可以從任何其他基高效計算。因此，埃爾米特正規形是公鑰基的最佳選擇 [Mic01]。
在 GGH 加密方案中，發送者使用公鑰選擇一個"隨機"格點 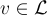，以某種方式編碼消息，然後向其添加一些小誤差 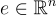，讓密文為 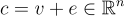。誤差足夠小，使得 c 比任何其他格點更接近 v，因此密文明確表示消息，並且從 c 恢復 v 是有界距離解碼問題的隨機實例。接收者使用其對好基的知識可以輕鬆解碼 c 回到 v 並恢復消息。為了安全性，可以假設僅知道壞基的竊聽者無法解碼 c，甚至無法了解 v 的任何信息，這意味著消息被隱藏。
在 GGH 簽名方案中，要簽名的消息被映射到一個點 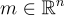，例如通過適當的公開哈希函數。簽名者然後使用其好基找到一個相對接近 m 的格向量 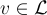，作為簽名。驗證者僅使用公開的壞基可以驗證 v 是一個格向量並且足夠接近 m。為了安全性，可以假設僅知道壞基和一些先前消息-簽名對的偽造者無法找到足夠接近未簽名消息 m′ 的格向量。然而，事實證明，這個假設是錯誤的，如 [NR06] 中最嚴重地展示的那樣。主要問題是簽名洩露了關於秘密"好"基的幾何形狀的重要信息，經過相對較少的簽名後，對手最終可以完全恢復秘密基，從而偽造任意消息的簽名。

NTRU 與 GGH 的結合:
遵循 [GGH97] 的思想，使用 NTRU 類型格的緊湊基於環的實例在 [HPS01, HHGP+03] 中提出。這些方案受到各種實際攻擊，除了適用於所有 GGH 類型簽名的通用攻擊。值得注意的是，第二個提案 [HHGP+03] 包括一種"擾動"技術，旨在使簽名洩露關於私鑰的信息顯著減少（以更大的密鑰和參數為代價）。主要思想是，將哈希的消息 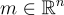解碼到附近格向量 的算法顯著不那麼線性，因為它涉及兩個不相關的格基。然而，[NR06] 的思想被擴展以也破解這個變體，無論是在漸進意義上 [MP"SW09, Wan10] 還是在實踐中 [DN12b]。

Micciancio的緊湊單向函數
受到 NTRU 設計思想和效率的啟發，米奇安西奧 [Mic02] 在 2002 年發表的工作中修改了阿傑塔 [Ajt96] 的單向/抗碰撞函數，使其在形式為 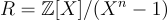的多項式環上工作，並展示了這如何帶來主要的效率改進，即準線性 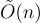的密鑰大小和運行時間（改進準二次 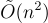）。米奇安西奧還證明，修改後的函數是單向的，假設某些 n 維循環格上的近似問題在最壞情況下是難解的。
與阿傑塔的原始函數不同，並且有些奇怪的是，[Mic02] 的安全性證明表明修改後的函數是單向的，但不是抗碰撞的（這是一個比單向性嚴格更強的屬性）。兩項獨立的後續工作 [PR06, LM06] 表明，[Mic02] 中定義的函數實際上不是抗碰撞的，但稍微修改構造以在其他環上工作可以使其抗碰撞，在相同類型的最壞情況下複雜性假設下。所有這些工作僅限於構造單向和抗碰撞哈希函數；它們沒有獲得任何公鑰加密方案。然而，它們的思想是環-LWE 發展的重要先驅，後者確實支持加密。

雷格夫對阿傑塔-德沃克的改進
在 2003 年的一項重要工作中，雷格夫 [Reg03] 對阿傑塔和德沃克 [AD97] 的結果進行了幾項改進。雷格夫的工作最顯著地引入了高斯測度（概率分佈）和格上的調和分析到密碼方案的設計和分析中，建立在 Banaszczyk [Ban93, Ban95] 在數學中的使用之上。這些技術產生了顯著更簡單的算法和分析，以及底層最壞情況下格問題的更緊密的近似因子。更具體地說，阿傑塔和德沃克表明破解他們的密碼系統意味著能夠在 n 維格上解決某些大多項式 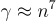的 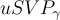，而對於雷格夫的系統，近似因子僅為 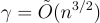。由於 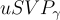僅在 γ 減小時變得更難，這意味著雷格夫的密碼系統在潛在更溫和的複雜性假設下可證明安全。此外，密碼系統本身的改進設計能夠抵抗已知的密碼分析攻擊，密鑰、密文和運行時間比阿傑塔-德沃克更小。然而，密碼系統的漸進成本基本保持不變，公鑰大小為 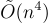，私鑰和密文大小為 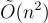，加密和解密的運行時間相應匹配。

[Ajt96] M. Ajtai. Generating hard instances of lattice problems. Quaderni di Matematica, 13:1–32,
2004. Preliminary version in STOC 1996

[AD97] M. Ajtai and C. Dwork. A public-key cryptosystem with worst-case/average-case equivalence.
In STOC, pages 284–293. 1997.

[AD07] M. Ajtai and C. Dwork. The first and fourth public-key cryptosystems with worst-case/averagecase equivalence. Electronic Colloquium on Computational Complexity (ECCC), 14(97), 2007.

[NS98] P. Q. Nguyen and J. Stern. Cryptanalysis of the Ajtai-Dwork cryptosystem. In CRYPTO, pages 223–242. 1998.

[HPS98] J. Hoffstein, J. Pipher, and J. H. Silverman. NTRU: A ring-based public key cryptosystem. In
ANTS, pages 267–288. 1998.

[CS97] D. Coppersmith and A. Shamir. Lattice attacks on NTRU. In EUROCRYPT, pages 52–61.
1997.

[SS11] D. Stehle and R. Steinfeld. Making NTRU as secure as worst-case problems over ideal lattices. ´
In EUROCRYPT, pages 27–47. 2011.

[McE78] R. J. McEliece. A public-key cryptosystem based on algebraic coding theory. DSN Progress
Report 42-44, Jet Propulsion Laboratory, 1978.