前情提要

昨天已經介紹完 BatchNrom, LayerNorm，

參考文章:
https://www.cnblogs.com/rossiXYZ/p/18774865

https://www.zhihu.com/question/14925347536/answer/124415677636

1. RMSNorm

沒錯又是這張圖，在第十天介紹過，目前主流 LLM 都改用 RMSNorm，那是為什麼?

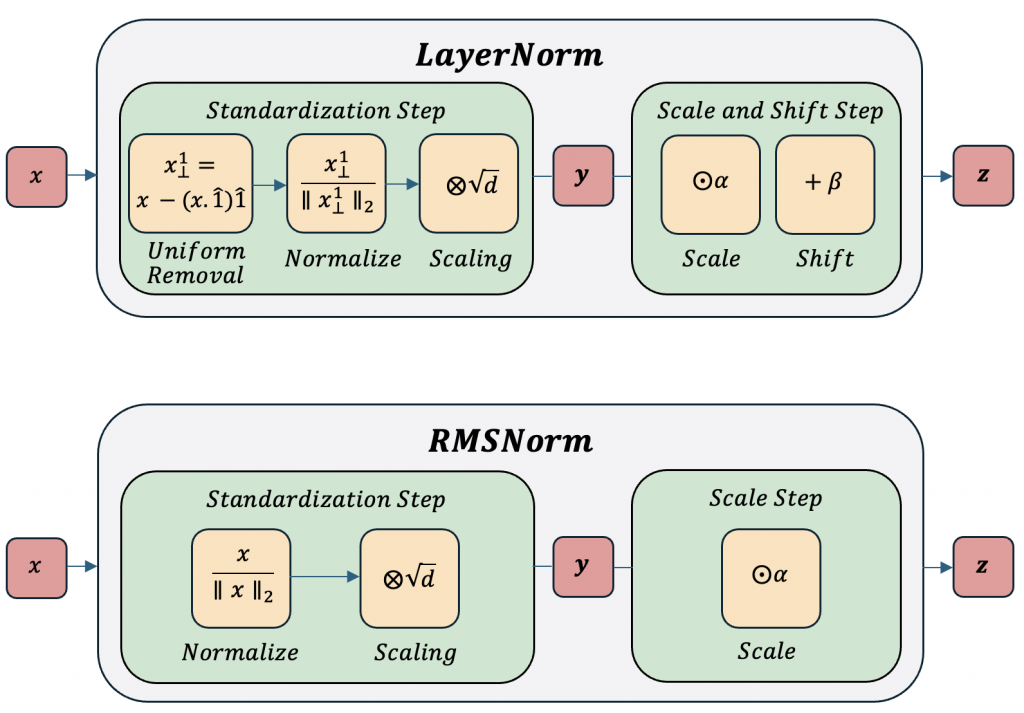
老樣子先來兩張圖，分別是比較 LayerNorm 跟 RMSNorm，在 RMSNorm 設計上更精簡，少了 “mean subtracting”，在 LLM 或者其他研究，數據顯示會發現減掉平均這步驟是冗餘的，在 loss 或評分上是差不多的，而且因為少了這步驟的運算，整體的計算更快更適合 LLM 的訓練。
  
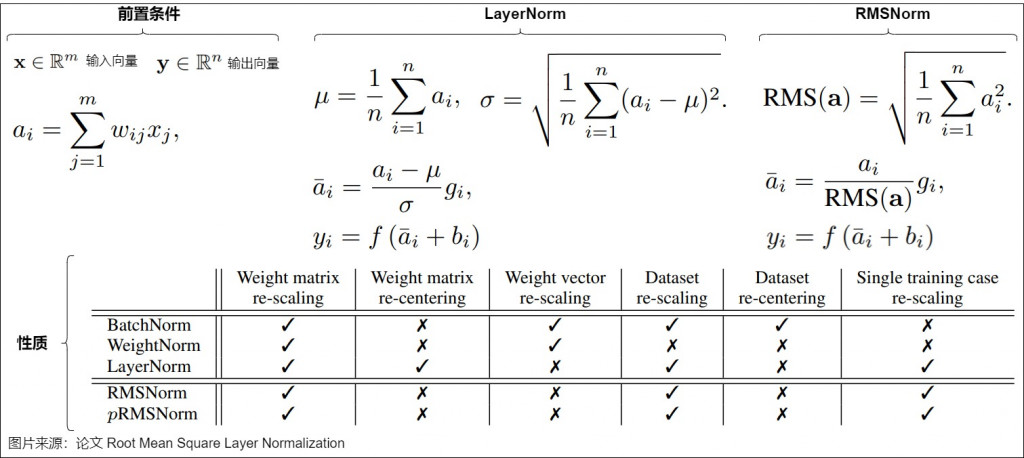
  上圖是採用 L2 norm 在乘上 scaling，會等於下圖直接算平方總合開根號。
圖片來源: https://arxiv.org/html/2409.12951v1
  

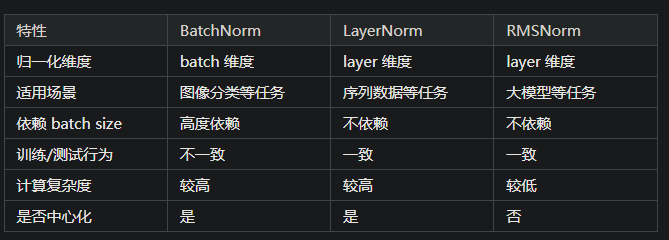
總結一下這兩天學的

2. DyT

Dynamic Tanh (DyT) 是由 Meta 提出的論文 Transformers without Normalization，當中透過 DyT 來取代 LayerNorm。

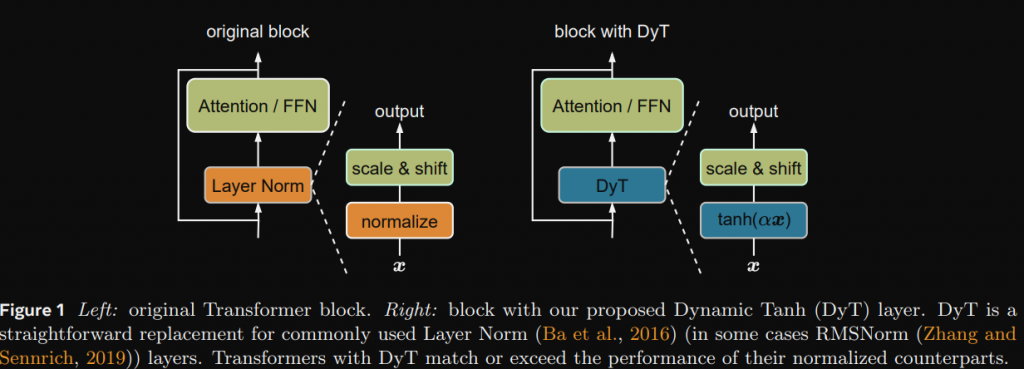
論文當中將輸入-輸出映射呈現出類似 tanh 的 S 型曲線，既然是類似 tanh 曲線，所以他們將 LN 用 tanh 做取代，並嘗試了一些任務，確實效果差不多，但計算量更低。


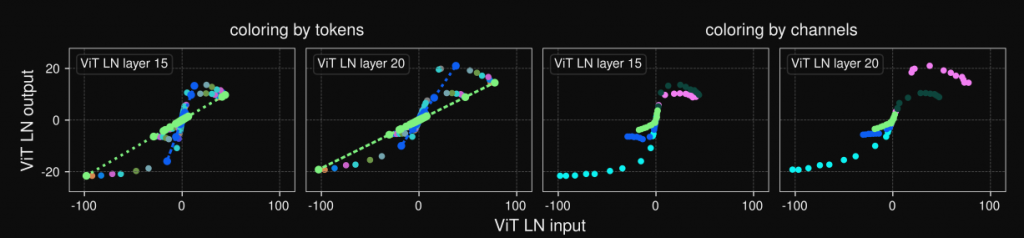
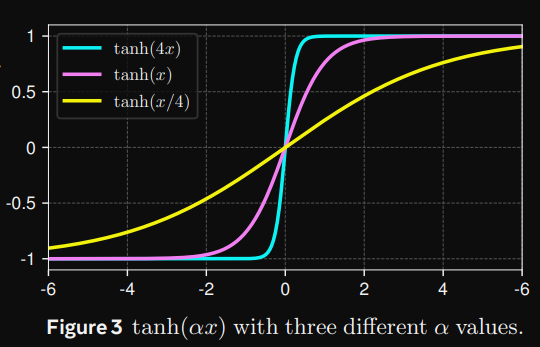
在這評論區當中有很多大神，當中蘇神(提出RoPE的作者)認為，Normalization 無腦地穩定了模型的前向傳播，要把它拿掉或者取代掉不太現實，除非可以在各個主流模型都測出一個分數，那因為 Meta 的論文針對 LLM 其實只有拿最一開始的 LLama 模型做測試而已，這部分我也覺得還不能夠說服大家 DyT 比較好，不過我覺得就當個想法多認識也不錯。

3. RMSNorm 實作

這邊用 RMSNorm 實作來講解

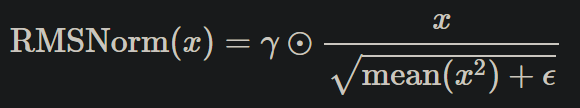
步驟:

1. 定義最基本的 class (init + forward) → 問自己 x 輸入的維度是多少
2. 只需要一個 scale 名為 gamma → 宣告 nn.Parameter
   eps 防止方母為 0
3. 在 forward 準備要做計算
4. 平方 → mean 平均 → 加上 eps → 開根號 → 倒數
5. 乘上 x
6. 乘上 gamma (可學習的參數)

import torch
from torch import nn

# step 1
class RMSNorm(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, x: torch.Tensor):
        '''
            B: batch size
            L: seq len
            D: embedding dimension
            x: (B, L, D) or (B, L, E)
        '''
        return

# step 2
class RMSNorm(nn.Module):
    def __init__(self, dim: int, eps: float = 1e-5):
        super().__init__()
        # 防止分母為 0
        self.eps = eps

        # 宣告一個 scale，初始化為 1 維度 dim
        self.gamma = nn.Parameter(torch.ones(dim))

    def forward(self, x: torch.Tensor):
        '''
            B: batch size
            L: seq len
            D: embedding dimension
            x: (B, L, D) or (B, L, E)
        '''
        return

# step 3
class RMSNorm(nn.Module):
    def __init__(self, dim: int, eps: float = 1e-5):
        super().__init__()
        # 防止分母為 0
        self.eps = eps

        # 宣告一個 scale，初始化為 1 維度 dim
        self.gamma = nn.Parameter(torch.ones(dim))

    def _norm(self, x: torch. Tensor):
        # 平方 x ** 2 or x.pow(2) → mean 平均 → 加上 eps → 開根號 → 倒數
        # sqrt -> 開根號, r -> 倒數
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x: torch.Tensor):
        '''
            B: batch size
            L: seq len
            D: embedding dimension
            x: (B, L, D) or (B, L, E)
        '''
        # 這裡會轉 float 和轉回去 -> 因為訓練可能是 bf16 或其他型態
        return self.gamma * self._norm(x.float()).type_as(x)
    
if __name__ == "__main__":
    x = torch.rand(2, 5, 3)
    norm = RMSNorm(x.size(-1))

    y = norm(x)
    print(f'x: {x}\n')
    print(f'y: {y}')

以下得到輸出:
然後請 gpt 幫我驗證一下對不對，因為我們初始 gamma 為 1，所以 y = x/RMS(x)，那 gamma 會跟著訓練做調整，因為他是可學習參數。

歸一化的部分就簡單介紹到這裡，今天就到這裡囉~