前情提要

昨天介紹了數據類型以及如何簡單模型模型參數量，最後有提到激活的部分，我們針對這個更加詳細介紹。

參考連結 & 圖片來源:
https://www.stat.cmu.edu/~ryantibs/convexopt-F18/scribes/Lecture_19.pdf
https://www.cnblogs.com/rossiXYZ/p/18785615

1. FLOPs

一個 FLOP 代表一個基本的運算單元: 浮點數的加減乘除。
FLOPs (Floating Point Operations per Second)：這是一個衡量計算機運算速度的指標，是一個粗略的測量，而不是精確的計算。

1.1 Vector-vector operations

兩個向量 a, b，維度為 n

• 相加 a + b: 有 n 個元素相加，所以需要 n flops
• 內積 a^Tb: 有 n 個相乘，然後要把所有加起來需要 n - 1 個相加，所以需要 2n flops(會把 - 1 省略，因為只是粗略估計)。

1.2 Matrix-vector operations

A 維度為 (m, n), b 維度為 (n), 考慮一般 Ab:

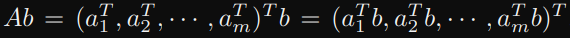
a1^Tb, a2^Tb, …, am^Tb → 每個都是 vector-vector operations，所以都需要 2n flops。
上面總共有 m 個 2n flops，所以總共 2mn flops。

1.3 Matrix-matrix product

A 維度 (m, n), B 維度 (n, p), 考慮一般 AB:

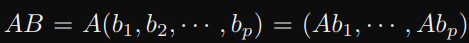
當中 Ab1, Ab2, …, Abp 都是 matrix-vector ，所以每一個都需要 2mn flops。
上面總共有 p 個 2mn flops，所以總共 2mnp flops。

我們用更簡單的表示 (▢, △) 內積 (△, ○) → 2▢△○
之後只需要把代號填入 ▢ △ ○ 即可，比較不容易搞混

2. forward 計算量

以下簡寫照我們之前常用的 (B, L, D)，參考文章使用 b, s, h

• B: batch size
• L: seq_len
• D: embedding dimension

計算 Q, K, V

輸入 (B, L, D) 然後與 linear 的 weight (D, D) 相乘，輸入的 B 可以最後再考慮，先看 (L, D) (D, D) → 2LD^2 (把L, D, D 分別填到▢ △ ○而已哦)
此時再把 B 補回來變 → 2BLD^2
因為有 Q, K, V 三個，所以總共 6BLD^2

計算 QK^T

輸入分別為(B, L, D), (B, D, L) 一樣先不看 B
(L, D) (D, L) → 2DL^2 (把L, D, L 分別填到▢ △ ○而已哦)
此時再把 B 補回來變 → 2BDL^2

乘以 V

輸入分別為 (B, L, L), (B, L, D) 一樣先不看 B
(L, L) (L, D) → 2DL^2 (把L, L, D 分別填到▢ △ ○而已哦)
此時再把 B 補回來變 → 2BDL^2

O 線性映射

跟最一開始計算 Q, K, V 一樣，所以是 2BLD^2

FFN

升維: 輸入 (B, L, D) 和 weight (D, 4D) 一樣先不看 B
(L, D) (D, 4D) → 8LD^2 (把L, D, 4D 分別填到▢ △ ○)
此時再把 B 補回來變 → 8BLD^2
降維依此類推 → 8BLD^2

總結

所以總結上述，參考下圖參考文章的總結，計算複雜度隨著序列長度的增加呈二次方增加的趨勢 (QK^ T 和 乘以V)，這裡也是為什麼訓練 MHA 時長度不可以太長，因為記憶體需求量高。

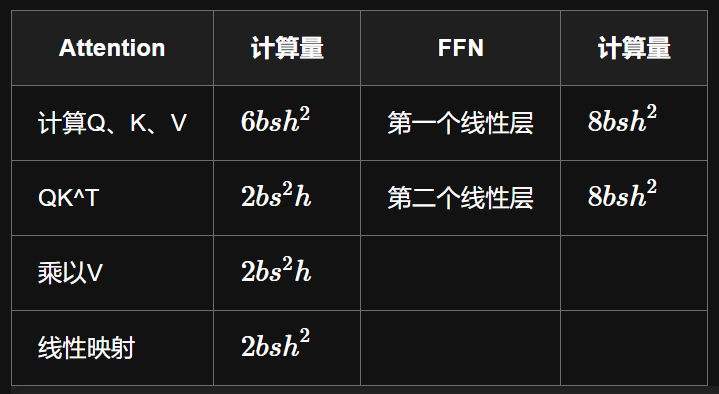
今天主要是簡單介紹一下如何計算模型在 forward 時的計算量，其實這一部份我一開始也是一頭霧水，只知道有序列長度二次方的關係，但後來自己跟著推導一次，然後使用 ▢ △ ○ 填入英文的代號，就懂那些是如何計算出來的，希望這個過程也能幫助到你了解，今天就到這裡囉~