為什麼要談 Positional Encoding？
在上一篇我們聊到 Self-Attention，它能讓模型捕捉句子中詞與詞之間的關聯。但這裡有個問題：
自注意力機制本身不懂「順序」。
對比一下：
RNN / LSTM：天生就是一個詞接一個詞地處理，所以模型自帶「先後順序」的感覺。
Transformer：一次性把整句話丟進去，模型在一層中同時看所有詞，沒有「先誰後誰」的直覺。
這會導致什麼問題呢？
舉個例子：
「我愛你」
「你愛我」
在我們看來，這兩句意思完全不同。但對 Transformer 來說，如果沒有告訴它「位置」的資訊，這兩句就是一堆字的集合（Bag of Words），結果模型根本分不清。
這就是為什麼需要 Positional Encoding 要給模型一個「座標系統」，告訴它每個詞的位置。

Positional Encoding 怎麼做？
Transformer 原始論文提供了一個數學設計:正弦與餘弦函數 (Sinusoidal functions)公式
它的公式長這樣：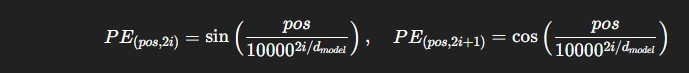

別急，看不懂很正常，我們先來用直觀方式來理解：
pos：單詞在句子中的位置（例如第 1 個詞、第 2 個詞…）。
i：向量的維度索引（不同維度有不同頻率）。
d_model：Embedding 向量的總維度。
結果是：每個位置會對應一個獨特的「波形編碼」。
不同維度用不同頻率的波，讓模型既能看到「局部差異」（短距離關係），也能看到「全局趨勢」（長距離結構）。
如果畫出來，會是一組交錯的正弦曲線（正弦/餘弦波形圖）。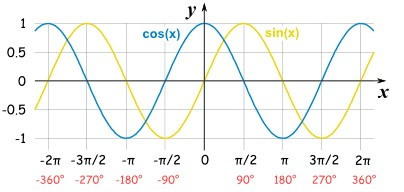

在前面的公式與簡單的正弦/餘弦圖中，我們大致理解了 Positional Encoding 的數學設計。
不過，實際上模型需要的並不是單純的波形，而是 將每個位置轉換成對應的向量。
如下圖所示：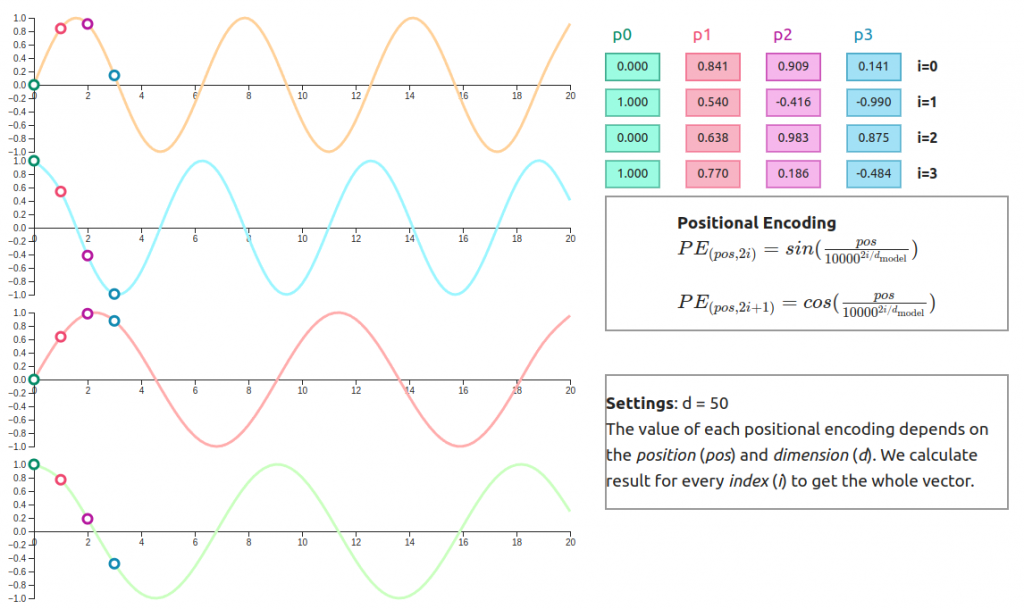

左邊的曲線代表不同維度（dimension）下的正弦/餘弦波形。
每個位置（例如 p0、p1、p2、p3）都會對應到一組獨特的數值，這些數值組合起來就是該位置的「編碼向量」。
右邊的表格就是具體的數值範例：同一句話中，第 0 個詞、第 1 個詞…都會拿到不同的向量。
這樣一來，模型就能夠同時「看懂」詞本身的語意（Embedding），以及它在序列中的位置（Positional Encoding）。
換句話說，這些位置向量是 Transformer 在處理整句話時的「座標系統」。

Positional Encoding 的好處
唯一性：每個位置都有獨特的向量，不會重複。
數學規律：因為是正弦/餘弦設計，模型可以「外推」到更長的序列。例如，訓練時只看過長度 100 的句子，但推理時遇到長度 120 的句子，仍然能生成合理的位置編碼。
簡單卻有效：不需要額外學參數，只靠數學函數就能讓模型知道順序。

後來的發展
雖然原版 Transformer 用的是正弦位置編碼，但後來研究者也提出了不同的替代方案：
Learnable Position Embedding（可學習的位置向量）：讓模型自己學習怎麼表示順序，效果往往更好。
Relative Positional Encoding（相對位置編碼）：關注「詞與詞的距離」，而不是絕對位置，這對翻譯、對話等任務很有幫助。

不論是絕對位置還是相對位置，核心思想都是：
一定要把「順序」這個知識加進模型裡，否則句子的意思就無法被正確理解。

比如說:
可以把 Transformer 想像成一個學生，他超會分析每個詞之間的關係（Self-Attention），但他先天沒有時間觀念。
Positional Encoding 就像在課本上幫詞加上「編號」，讓學生知道「第 1 個詞是誰、第 2 個詞是誰…」，這樣他才能理解「我愛你」和「你愛我」的差別。

結語
Positional Encoding 的核心就是 —— 幫詞加上座標。
它補足了自注意力缺乏順序感的缺陷，讓 Transformer 能同時理解：
關聯（詞與詞的語意關係）
順序（詞在句子中的排列結構）
其中三種主要的方式：
正弦位置編碼：數學優雅，可外推出更長序列
可學習位置嵌入：靈活，能讓模型自己學出最適合的表示
相對位置編碼：更貼近語言需求，關注詞與詞之間的距離
雖然方法不同，但目標一致，就是為了讓 Transformer 能正確理解語言的結構。
理解了 注意力（關聯） 和 位置（順序） 之後，我們下一步將探討：Transformer 如何透過大規模語料的訓練，真正學會語言知識。