前言
昨天我們介紹了分類任務，今天要從數學和統計的角度認識一個經典的分類演算法——邏輯迴歸 (Logistic Regression)。
為了理解它，先要知道它的前身——線性迴歸 (Linear Regression)

一、線性迴歸是什麼？

1. 為什麼叫「線性」？
   在線性迴歸中，我們假設輸入特徵 𝑥 與輸出 𝑦 之間有一個 線性關係：y=w⋅x+b

   • 𝑥：輸入特徵（例如讀書時數）
   • y：輸出目標（例如考試分數）
   • w：斜率，代表每增加一單位 𝑥時，𝑦大約增加多少
   • b：截距，表示 𝑥=0 時的基準值

   因為公式是直線關係，所以叫「線性」。

2. 為什麼叫「迴歸」？
   「迴歸」的意思是「用一條線去描述資料的趨勢，讓它盡量貼近所有資料點」。
   舉例：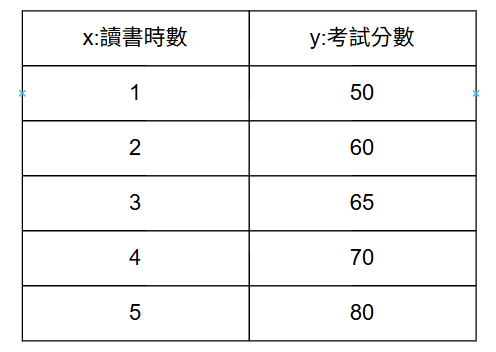
   
   線性迴歸可能得到公式：y=6x+45(如下圖)
   意思是：每多讀一小時書，分數大約多 6 分；完全不讀書也可能得到 45 分。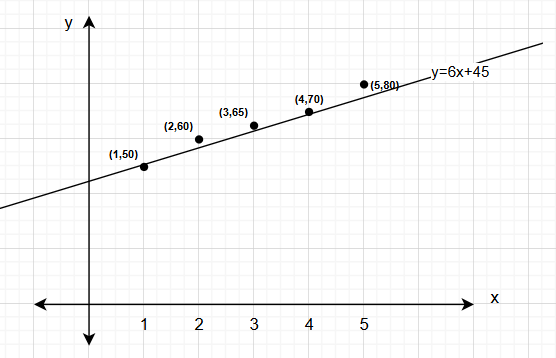
   

3.為什麼線性迴歸不適合做分類？

線性迴歸很擅長預測數字型的結果，比如考試分數或氣溫，但如果我們要預測「是否通過考試（是/否）」，直接用線性迴歸就不太適合，原因有兩個：

(1)預測結果可能不合理

• 線性迴歸算出來的答案可能小於 0 或大於 1，但「通過的機率」必須介於 0 到 1 之間。

(2)無法反映機率的變化曲線

• 實際上，隨著讀書時間增加，通過考試的機率會慢慢上升，越多越可能通過，但不會一直線性增加到無限大。

• 線性模型只能畫一條直線，不能呈現這種「慢慢增加、接近 1」的效果。

由於上述原因，因此改用邏輯迴歸：

• 它會把線性計算的結果轉換成 0 到 1 的機率。

• 然後只要設定一個臨界點（例如 0.5），就可以判斷「會通過」或「不會通過」。

這樣既保留了線性計算的簡單，又能合理地做二元判斷。

二、邏輯迴歸是什麼？

邏輯迴歸就是「把線性迴歸改造成可以做分類的工具」，讓模型能預測「是/否」這種二元結果。

1. 核心公式
   
   其中：
   z=w1​x1​+w2​x2​+⋯+wn​xn​+b

• X=(x1​,x2​,...,xn​)：輸入特徵（影響結果的因素）
• w1​,w2​,...,wn​：每個特徵的權重，代表對結果的影響力
• b：偏差或基準值
• z：線性組合結果，把所有特徵加權總和再加上偏差，得到一個數字
• e：自然常數，約等於 2.718，用於計算 Sigmoid 函數
• P(Y=1∣X)：在已知特徵 X 的條件下，事件 Y 發生的機率
• σ(z)：Sigmoid 函數(如下圖)，把 z 轉換成 0~1 之間的機率
  

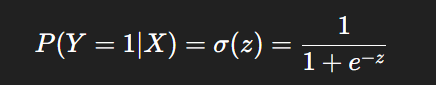
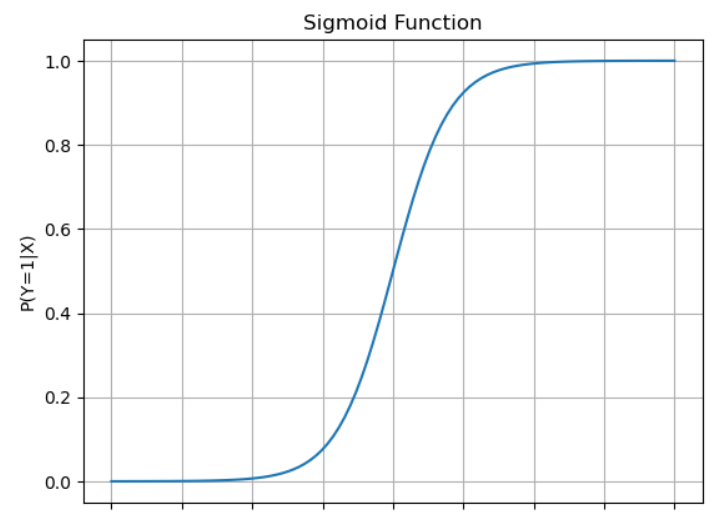
2. 偏差 b 的意義
   b 就像模型的「起始值」，代表當所有特徵 x 都是 0 時，事件發生的機率
   它幫助 Sigmoid 函數把曲線上下移，讓模型更靈活調整預測機率
   範例：
   假設每天讀書 0 小時，b = -1
   計算 z = 0 + b = -1 → 套入 Sigmoid → P(Y=1|X) ≈ 0.27
   這表示「完全沒讀書的情況下，通過考試的機率約 27%」

3. P(Y=1|X) 的意義
   P(Y=1|X) 就是：「在已知特徵 X 的條件下，事件 Y 發生的可能性」
   舉例：
   X = {每天讀書 5 小時，睡眠 7 小時}
   Y = 1 → 通過考試
   P(Y=1 | X) = 0.88 → 意思是「在這個讀書與睡眠條件下，通過考試的機率大約 88%」

4. 為什麼不用 P(Y|X)
   P(Y|X) 表示「在條件 X 下，Y 的整體機率分布」，包含所有可能結果
   二元分類時，Y 可能是 0 或 1
   P(Y|X) = {P(Y=0|X), P(Y=1|X)}
   P(Y=1|X) 只關心「事件發生的機率」
   因為 P(Y=0|X) = 1 - P(Y=1|X)，已經自動知道了
   所以邏輯迴歸直接用 P(Y=1|X) 就夠了，簡單又清楚

5. 閾值（Threshold）判斷二元結果
   設定閾值，例如 0.5：
   P ≥ 0.5 → 預測「會通過」
   P < 0.5 → 預測「不會通過」
   閾值可以依需求調整，影響模型的分類結果
   範例：
   P(Y=1|X) = 0.88 → 0.88 ≥ 0.5 → 預測「會通過」
   P(Y=1|X) = 0.3 → 0.3 < 0.5 → 預測「不會通過」

6. 計算過程與範例

   假設我們只有一個特徵 𝑥（每天讀書時數），權重 w = 0.8，偏差 b = -2：

• 計算線性組合 z：
  讀 5 小時書 → z = 0.8 * 5 + (-2) = 2

• 套入 Sigmoid 函數：
  P(Y=1|X) = 1 / (1 + e^-2) ≈ 0.881

• 判斷二元結果（閾值 0.5）：

  P ≥ 0.5 → 預測「通過」
  P < 0.5 → 預測「不通過」

7. 簡單總結

• 線性迴歸：預測數字結果

• 邏輯迴歸：先線性計算 z → Sigmoid → 機率 → 閾值判斷二元結果

• P(Y=1|X) = 在已知特徵 X 下，事件發生的機率

• P(Y|X) 是機率分布，二元分類時不必算完整分布

• 這樣既保留線性計算的簡單，又能合理做二元判斷

小結
今天我們用「讀書時數與考試結果」的例子，介紹了邏輯迴歸的運作方式。它的核心是利用 Sigmoid 函數把線性計算結果轉換成 0～1 的機率，再結合 偏差 b 與 閾值判斷二元結果。雖然邏輯迴歸概念簡單，但在實務上依然很常用，也是學習更進階分類模型的重要基石。
後續章節，我們會用程式實作邏輯迴歸，並介紹可以使用的工具與程式庫，讓大家把理論應用到實際案例中。