前言
昨天我們學習了如何調整邏輯迴歸的超參數，並透過交叉驗證了解模型在未見資料上的穩定性。今天，我們將針對這些專有名詞做深入解釋，包括正則化、梯度以及求解器（Solver），並用簡單數學例子幫助理解，讓模型調參不再只是設定數值，而是能夠理解背後的原理。

一、正則化（Regularization）
什麼是正則化？
正則化是一種在模型訓練時加入限制的技術，目的是避免模型過度擬合（Overfitting），讓模型在新資料上表現更穩定。它會「懲罰」權重過大的特徵，避免模型過度依賴某些特徵。

簡單說明
想像你在寫考試，手上有一本很厚的參考書。如果你背太多細節，考試時可能寫得超完美，但下一次換一份新題目你就答不出來。這就是「過度擬合」——記住太多細節，反而無法舉一反三。

正則化的作用，就像是老師規定「考試只能用重點整理」，不能全抄參考書。這樣一來，你不會太依賴某一小段資訊，而是能把知識用得更靈活。

把上述觀點套用在模型訓練中：
假設模型在計算的時候，會給每個特徵一個「權重」當作重要性。正則化就是在最後的計算裡，加上一個「懲罰項」，避免權重太大：

• L2 正則化：把權重平方後加起來，讓權重盡量小。
• L1 正則化：把權重的絕對值加起來，讓其中一些權重直接變成 0，就像自動幫你刪掉沒用的特徵。

L2 就像提醒你筆記要盡量簡潔，每個重點都別寫太長；L1 則像是直接幫你刪掉一些不重要的章節。

數學範例
假設我們的邏輯迴歸損失函數（Loss Function）為：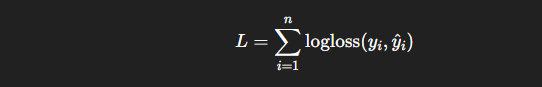

加入 L2 正則化後，損失函數變成：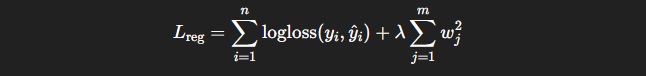

• λ → 正則化強度
• 𝑤𝑗 → 每個特徵的權重
• 當 𝜆 大 → 權重受限制 → 模型簡單
• 當 𝜆 小 → 權重自由 → 模型較複雜
  L1 正則化則是 ∑∣𝑤𝑗∣，會讓部分權重變 0，達到特徵篩選效果。

Python 示例

from sklearn.linear_model import LogisticRegression

# L2 正則化 (預設)
model_l2 = LogisticRegression(penalty='l2', C=1.0)

# L1 正則化
model_l1 = LogisticRegression(penalty='l1', solver='liblinear', C=1.0)

二、梯度（Gradient）
什麼是梯度？
梯度是一個向量，告訴我們損失函數在每個權重方向上增加或減少最快的方向。在訓練過程中，我們利用梯度更新權重，使損失函數下降，模型預測更準確。

簡單來說
想像你站在一座山上，要走到山谷最低點。梯度就是告訴你「哪個方向最陡、往那裡走能最快下山」。在模型裡，我們要找到一組最佳的權重，讓誤差最小，而梯度就是指引方向的路標。

把上述觀點套用在模型訓練中：
如果誤差公式是：
L(w) = w²
假設它的斜率（梯度）就是：2w

• 當 w=3 → 梯度=6，代表要往左邊走（減少 w）才會下降
• 當 w=-2 → 梯度=-4，代表要往右邊走（增加 w）才會下降

數學範例
假設損失函數
𝐿(𝑤)=w²，則梯度為：dL/dw=2w

• 當 𝑤=3 → 梯度 = 6 → 告訴我們往負方向減少
• 當 𝑤=−2 → 梯度 = -4 → 告訴我們往正方向增加

Python 更新權重示意

# 假設 w=3, learning_rate=0.1
w = 3
grad = 2 * w
w_new = w - 0.1 * grad  # w_new = 3 - 0.6 = 2.4

三、優化算法（Solver）
什麼是 Solver？
Solver 是用來計算最佳權重的算法。在邏輯迴歸中，我們希望找到一組權重，使損失函數最小。不同的 Solver 採用不同的數值方法，會影響收斂速度、支援的正則化類型以及大資料表現。

常見 Solver 及特性：

• lbfgs
  • 基於擬牛頓法（Limited-memory BFGS）
  • 適合中小資料集
  • 支援 L2 正則化
  • 收斂速度快，數值穩定
  • 不支援 L1 正則化
• liblinear
  • 基於線性分類器的座標下降法
  • 適合小型資料集
  • 支援 L1 與 L2 正則化
  • 計算簡單，適合稀疏資料
• saga
  • 基於隨機平均梯度下降法（Stochastic Average Gradient）
  • 適合大型資料集
  • 支援 L1、L2 與 ElasticNet 正則化
  • 對高維度稀疏資料表現良好
• newton-cg
  • 牛頓法變種，使用二階導數資訊
  • 適合中大型資料集
  • 支援 L2 正則化
  • 收斂快，但記憶體需求高
• sag
  • 基於隨機平均梯度下降（Stochastic Average Gradient）
  • 適合大型資料集
  • 支援 L2 正則化
  • 記憶體需求低，速度快

選擇建議：

• 資料量小 → liblinear 或 lbfgs
• 資料量大 → saga 或 sag
• L1 正則化 → liblinear 或 saga
• 需要 L2 → 大部分 solver 都可以，但 lbfgs 與 newton-cg 收斂穩定

Python 範例

# lbfgs 適合中小資料，支援 L2
model_lbfgs = LogisticRegression(solver='lbfgs', max_iter=500, C=1.0, penalty='l2')

# liblinear 適合小資料，支援 L1
model_liblinear = LogisticRegression(solver='liblinear', max_iter=500, C=1.0, penalty='l1')

# saga 適合大資料，支援 L1、L2
model_saga = LogisticRegression(solver='saga', max_iter=500, C=1.0, penalty='l1')

小結
今天我們認識了正則化、梯度與 Solver。正則化可以降低模型過度擬合的風險，梯度像地圖一樣指引我們往誤差最小的方向前進，而 Solver 則是用來計算最佳權重的演算法。理解這些原理後，超參數調整不再只是「調數字」，而能真正掌握模型背後的學習機制。

在後續章節，我們將延續監督式學習的主題，介紹更多常見演算法，並探討演算法在多類別分類上的應用。