前言
昨天我們完成了邏輯迴歸模型的建立，並試著用它預測單筆資料。今天，我們將深入探索模型內部，主要目標有三個：

1. 了解特徵對模型預測的影響
2. 全面評估模型在測試資料上的表現
3. 學會解讀混淆矩陣和常用評估指標
   透過今天的分析，我們不僅知道模型的準確率，也能理解模型是如何做出判斷，哪些地方可能需要改進。

一、分析特徵權重（Feature Coefficient）
為什麼要看特徵權重？

邏輯迴歸會對每個特徵計算一個「權重（coefficient）」，數字正負表示特徵對預測結果的影響方向：

• 正值 → 該特徵會增加預測為正例（例如 1 或「惡性」）的機率
• 負值 → 該特徵會降低預測為正例的機率

這樣做的目的：

• 知道哪些特徵最重要，增加模型可解釋性
• 幫助後續特徵選擇或改進模型
• 讓模型不是黑箱，我們可以理解它的判斷邏輯

程式碼範例與說明

import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression

# 建立模型，設定最大迭代次數為500
# max_iter=500 是為了確保模型能收斂，避免迭代不足導致警告
model = LogisticRegression(max_iter=500)

# 用訓練資料訓練模型
# fit() 會自動調整每個特徵的權重，使模型能夠盡量正確預測 y_train
model.fit(X_train, y_train)

# 取得模型學到的權重
coefficients = model.coef_[0]

# 生成特徵名稱，如果使用 NumPy 陣列沒有 columns 屬性
feature_names = [f"Feature {i}" for i in range(X_train.shape[1])]

# 列出每個特徵與其權重
for name, coef in zip(feature_names, coefficients):
    print(f"{name}: {coef:.3f}")

程式碼解釋

• LogisticRegression(max_iter=500)
  • 建立一個邏輯迴歸模型
  • max_iter 指最大迭代次數，邏輯迴歸會反覆調整權重直到收斂
• model.fit(X_train, y_train)
  • 用訓練資料讓模型學習
  • X_train：特徵資料（可能是數值型、標準化後）
  • y_train：對應的目標值
  • 內部會自動計算每個特徵的權重（coefficient）
• model.coef_[0]
  • 拿到模型學到的每個特徵權重
  • 是一個數字陣列，順序對應 X_train 的特徵
• feature_names = [f"Feature {i}" for i in range(X_train.shape[1])]
  • 如果沒有 DataFrame 的欄位名稱，直接生成簡單名稱方便列印
• for name, coef in zip(feature_names, coefficients)
  • 對應每個特徵名稱和權重列印出來

可視化特徵權重

plt.figure(figsize=(8,5))
plt.bar(feature_names, coefficients)
plt.xlabel("特徵")
plt.ylabel("權重")
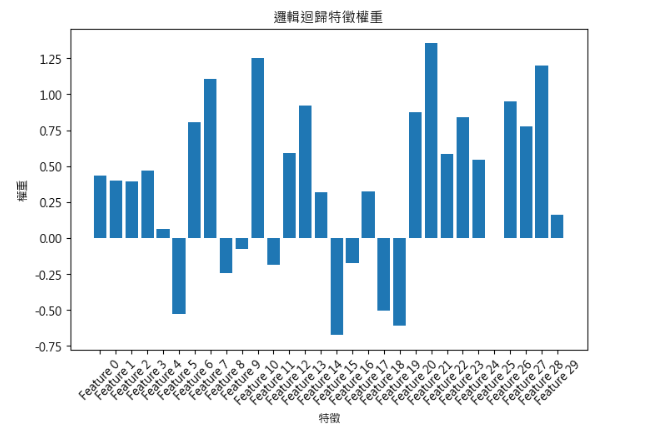
plt.title("邏輯迴歸特徵權重")
plt.xticks(rotation=45)
plt.show()

解釋：

• 畫出條形圖可以直觀看到哪些特徵影響最大
• 權重越高（正或負）代表對預測結果的影響越大
• 幫助我們做特徵篩選或調整

二、混淆矩陣（Confusion Matrix）與分類評估指標
正例（Positive）與負例（Negative?
在分類問題中，我們通常會把目標分成兩類：
1.正例（Positive, P）
代表我們關注的目標事件發生
例子：

• 偵測腫瘤是否惡性 → 惡性是正例
• 銀行貸款預測 → 會違約是正例
• 郵件分類 → 垃圾郵件是正例

2.負例（Negative, N）
代表目標事件未發生
例子：

• 偵測腫瘤 → 良性是負例
• 銀行貸款 → 沒有違約是負例
• 郵件分類 → 一般郵件是負例

為什麼要區分正負例？

• 計算 TP、FP、TN、FN 時必須知道哪類是正例、哪類是負例
• 某些應用中，正例比負例重要，例如醫療診斷、詐騙檢測
• 有助於計算精確率（Precision）、召回率（Recall）、F1 分數

數學例子
假設我們要預測腫瘤是否為惡性（正例 = 惡性，負例 = 良性），測試資料有 10 筆：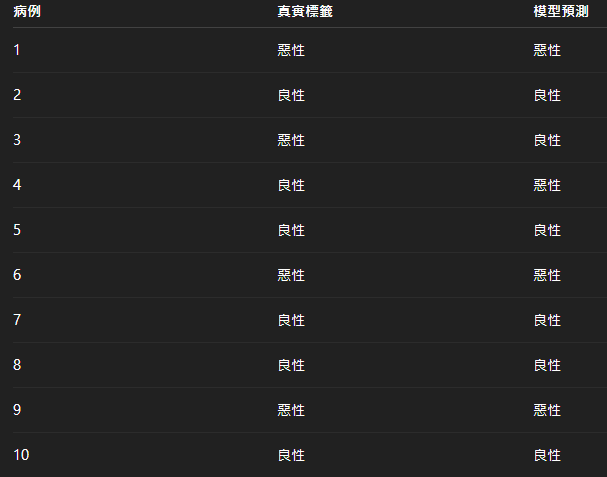

• 正例（P, 真實惡性） = 病例 1, 3, 6, 9 → 共 4 筆
• 負例（N, 真實良性） = 病例 2, 4, 5, 7, 8, 10 → 共 6 筆
  計算 TP、FP、TN、FN：
• TP（True Positive, 真陽性）= 3（病例 1, 6, 9）
• FP（False Positive, 假陽性）= 1（病例 4）
• TN（True Negative, 真陰性）= 4（病例 2, 5, 7, 8）
• FN（False Negative, 假陰性）= 1（病例 3）

常用分類評估指標公式
準確率（Accuracy）
衡量模型整體預測正確的比例：Accuracy=(TP+TN)/(TP+TN+FP+FN)
精確率（Precision）
衡量模型預測為正例的樣本中，有多少是真正的正例：Precision=𝑇𝑃/(𝑇𝑃+𝐹𝑃)
召回率（Recall / Sensitivity）
衡量所有正例中，有多少被模型正確預測：Recall=𝑇𝑃/(𝑇𝑃+𝐹𝑁)
F1 分數（F1 Score）
精確率與召回率的調和平均，綜合考量模型的正例預測能力：F1 Score=2×Precision×Recall/(Precision+Recall)

程式碼範例

from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay
from sklearn.metrics import precision_score, recall_score, f1_score

# 使用模型預測測試集
y_pred = model.predict(X_test)

# 計算整體準確率
accuracy = accuracy_score(y_test, y_pred)
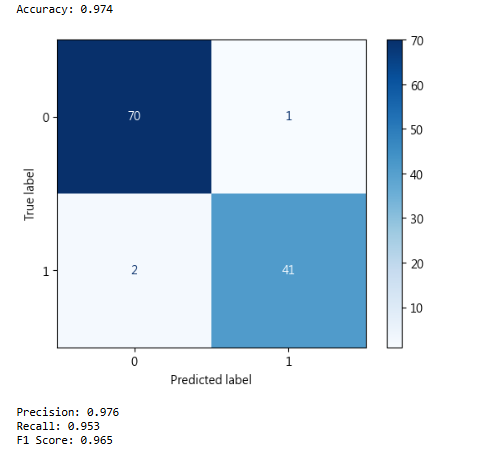
print(f"Accuracy: {accuracy:.3f}")

# 混淆矩陣
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=[0,1])
disp.plot(cmap=plt.cm.Blues)
plt.show()

# 計算其他指標
precision = precision_score(y_test, y_pred)  # 精確率
recall = recall_score(y_test, y_pred)       # 召回率
f1 = f1_score(y_test, y_pred)               # F1 分數

print(f"Precision: {precision:.3f}")
print(f"Recall: {recall:.3f}")
print(f"F1 Score: {f1:.3f}")

程式碼解釋

• y_pred = model.predict(X_test)
  • 將訓練好的模型用於測試資料
  • 得到每筆資料模型的預測結果（0 或 1）
• accuracy_score(y_test, y_pred)
  • 計算整體正確率
  • 公式：正確預測數 ÷ 總測試資料數
• confusion_matrix(y_test, y_pred)
  • 計算混淆矩陣，了解模型在哪些類別容易出錯
• ConfusionMatrixDisplay
  • 用圖表方式呈現混淆矩陣
  • 顏色深淺代表數值大小，更直觀
• precision_score, recall_score, f1_score
  • 精確率（Precision）：模型預測為正例中，有多少是真的正例
  • 召回率（Recall）：所有正例中，有多少被模型正確預測出來
  • F1 分數（F1 Score）：精確率與召回率的調和平均，衡量模型整體表現
    

小結
今天，我們完成了邏輯迴歸模型的深入分析：

• 特徵權重分析：知道哪些特徵對預測影響最大，增加模型可解釋性。
• 混淆矩陣與各項評估指標：全面了解模型在測試資料上的表現，發現模型可能錯誤分類的情況。
  這樣，我們不僅知道模型的準確率，還能清楚模型是如何做判斷，以及哪些地方需要改進。
  後續章節，我們將介紹 調整模型超參數與交叉驗證，讓模型在新資料上更穩定可靠，提升預測表現。