Day14 | Rosalind 生資解題 - 007. IPRB（Mendel‘s First Law）+組合數公式

題目連結：https://rosalind.info/problems/iprb/

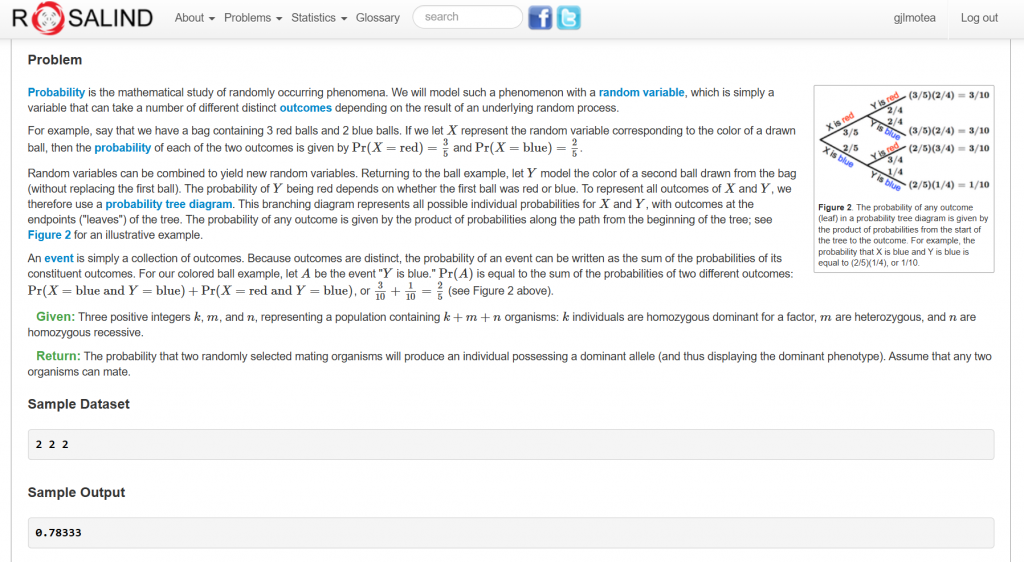
孟德爾第一定律（Mendel's First Law），是遺傳學中的分離律

題目輸入

2 2 2

輸出

0.78333

阿蛤？？？
當三個2擺在一起
怎麼計算也不會是這個數字吧？

不可能，絕對不可能！

這麼醜的數字0.78333到底是怎麼湊來的？
完了，連題目輸入範例都看不懂...

將浮點數轉為分數

首先，先搞清楚這個數字是哪個分數（幾分之幾）

0.78333 = 78.333% = 75% + 3.333%

換算成分數：

3/4 + 1/30 = 45/60 + 2/60 = 47/60

拿計算機起來驗算一下，果真等於0.87333

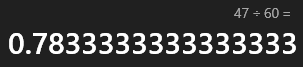
好的，心理比較有個底了，手邊已有個判斷材料

題目輸入的 2 2 2 代表 k, m, n

k individuals are homozygous dominant for a factor, m are heterozygous, and n are homozygous recessive.

• 純顯性型（homozygous dominant）：兩者均為顯性 => 顯性 x 顯性
• 異形合子（heterozygous）：兩者相異 => 顯性 x 隱性
• 純隱性型（homozygous recessive）：兩者均為隱性 => 隱性 x 隱性

也就是說，現在一個族群里有
2個AA（顯性 x 顯性）、2個Aa（顯性 x 隱性）、2個aa（隱性 x 隱性）

題目要計算任意交配後，子代呈現顯性的機率

機率計算

那機率怎麼計算呢？
先來計算交配方式有幾種

用總共６個生物做計算，隨機挑兩個生物來交配（不重複）有幾種方式？

C6取2 => C(6,2) = 6!/2!4! = 15

總共有15種配對方式

不對啊，既然15種配對方式，那怎麼會是分數47/60，分母是60？
大腦卡了一下。
哦！因為還要算上隱性顯性的機率
機率不一定都是整數(1 or 0)，會有出現小數的可能

棋盤方格法

棋盤方格法（或稱旁氏表、龐尼特方格, Punnett Square）
若為2個Aa（顯性 x 隱性）=> 子代機率則為75%顯性、25%隱性

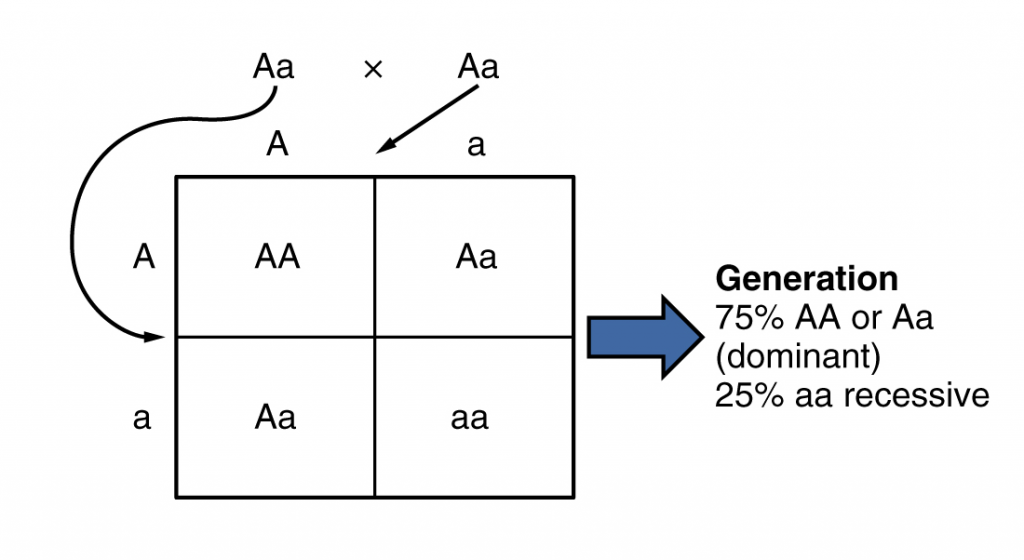
好，看來現在有各式各樣的棋盤方格要來計算惹
計算交配方式的機率

但是這一步，會讓大腦很亂、難以直接計算

因為，個體總共有這麼多：
2個AA（顯性 x 顯性）、2個Aa（顯性 x 隱性）、2個aa（隱性 x 隱性）

於是先把這群生物分成三坨
第一坨A、第二坨B、第三坨C

AA => 第A坨
Aa => 第B坨
aa => 第C坨

任選兩隻生物，有可能取到：
A+A坨、A+B坨、A+C坨
B+B坨、B+A坨、B+C坨
C+C坨、C+A坨、C+B坨

整理一下、將相同的放在一起：
AA、BB、CC 以及
AB、AC、BA、BC、CA、CB

用 A坨生物 的視角來看
他有這些交配的選擇（最終結果就是AA一次、AB兩次、AC兩次）

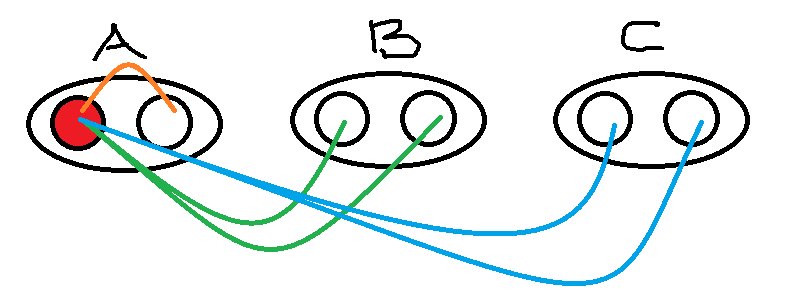
以 每一坨生物 的視角循環一輪後，會得出以下：
1次：AA、BB、CC
2次：AB、AC、BA、BC、CA、CB
數字加起來剛好為15（C6取2）種配對方式

接著，按照各式情境，對應的棋盤方格法

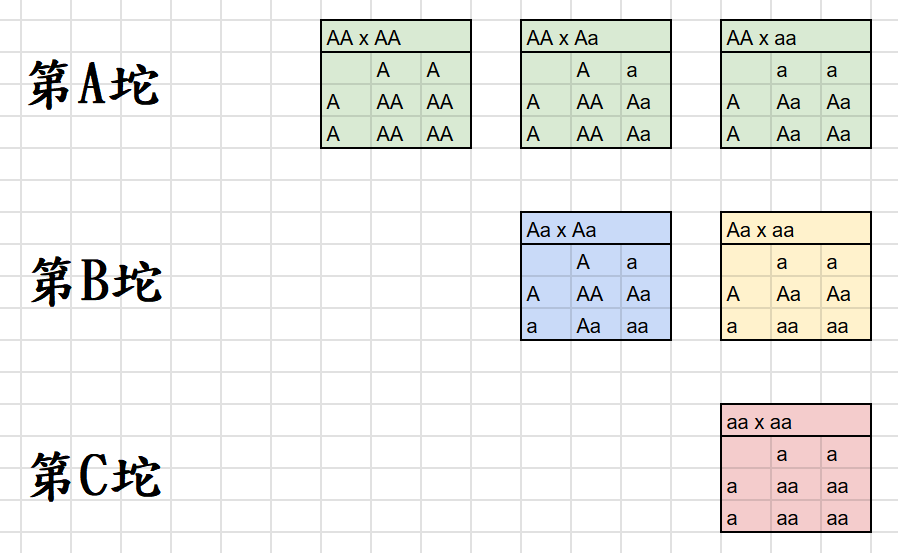
計算後代的顯性比例（４項分別對應四種不同底色）
AA x ?? = 100% 只要有碰到AA，後代機率一定是100%（綠色底）
Aa x Aa = 75% （藍色底）
Aa x aa = 50% （黃色底）
aa x aa = 0% （紅色底）

所以不管怎麼取，後代顯性都只會有以上四種機率

將機率帶入 配對可能性
AA、BB、CC：1次
AB、AC、BA、BC、CA、CB：2次 => 等同 AB、AC、BC 各取4次 ​

得出這張統計表

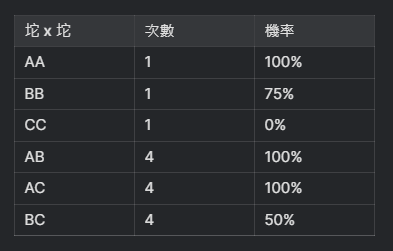
機率次數加總、除以總次數，就是答案了

( (100% + 75% + 0%)x1 + (100% + 100% + 50%)x4 )/ 15 = 0.78333

範例的輸出就是這麼來的

BUT，若換個數字
A、B、C三坨的數量分別是：1、2、3 個 的話
次數又會有所變化

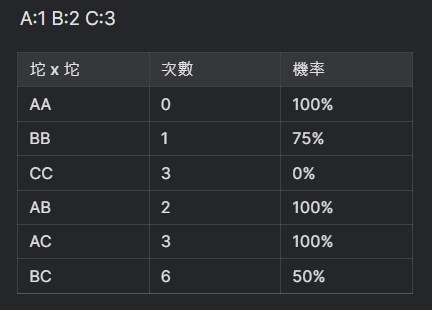
（因為A只有一隻、不可能跟自己交配，所以AA為0次）

有沒有公式

將以上的式子，換算成代數k, m, n套入的話，就會是這張圖表

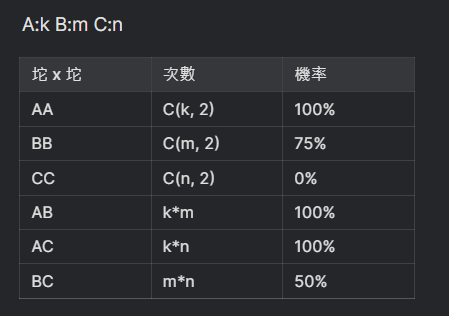
( (k．100%) + (m．75%) + (n．0%)
+ (2．k．m．100%) + (2．k．n．100%) + (2．m．n．50%) ) / total（C6取2）

程式碼：

解法一 math.comb()

使用math.comb()的方法來計算排列組合、C幾取幾

import math

k, m, n = 2, 2, 2

total = math.comb(k + m + n, 2)
kk = math.comb(k, 2)
mm = math.comb(m, 2)
nn = math.comb(n, 2)

print((kk * 1 + mm * 0.75 + nn * 0 + k * m * 1 + k * n * 1 + m * n * 0.5) / total)

這樣寫雖然精簡，但可讀性不佳
後來要改，會不知道這在計算個啥

BTW，另一個計算排列組合的數量，是 itertools.combinations()
這是會組出所有的排列組合，而不是可能性的總數（要再len()才會是總數）

import itertools

items = ['A', 'B', 'C']

combs = list(itertools.combinations(items, 2))

print(combs)  # [('A', 'B'), ('A', 'C'), ('B', 'C')]
print(len(combs))  # 3

解法二 itertools.combinations()

import itertools


def dominant_probability(k, m, n):
	# 產出所有基因池可能性
	pool = ['AA'] * k + ['Aa'] * m + ['aa'] * n  # ['AA', 'AA', 'Aa', 'Aa', 'aa', 'aa']

	total = 0
	count = 0  # 計算顯性後代(dominant offspring)的數量

	for a, b in itertools.combinations(pool, 2):
		total += 1

		pair = {a, b}  # 用集合去重複、不管先後順序
		# 1. ex: ('AA','AA') 變成 ('AA')
		# 2. ex: ('AA', 'Aa') 等同於 ('Aa', 'AA')

		print(pair)
		if pair == {'AA'}:
			count += 1
		elif pair == {'Aa'}:
			count += 0.75
		elif pair == {'aa'}:
			count += 0
		elif pair == {'AA', 'Aa'}:
			count += 1
		elif pair == {'AA', 'aa'}:
			count += 1
		elif pair == {'Aa', 'aa'}:
			count += 0.5

	return count / total


print(dominant_probability(2, 2, 2))

集合（set） 的特性是去重複、與前後順序無關

print({'AA', 'Aa'} == {'Aa', 'AA'})  # 為相同集合(set)

解法三 直觀機率累加

其實這道題也可以不用用到排列組合公式
畢竟C6取2，就是 C(6, 2) = 6x5 = 6x(6-1)

C(n,2) = n * (n-1)

最直觀的寫法如下
程式碼：

def dominant_probability(k, m, n):
	total = k + m + n

	prob = 0
	prob += (k / total) * ((k - 1) / (total - 1)) * 1  # AA x AA
	prob += (k / total) * (m / (total - 1)) * 1  # AA x Aa
	prob += (m / total) * (k / (total - 1)) * 1  # Aa x AA
	prob += (k / total) * (n / (total - 1)) * 1  # AA x aa
	prob += (n / total) * (k / (total - 1)) * 1  # aa x AA
	prob += (m / total) * ((m - 1) / (total - 1)) * 0.75  # Aa x Aa
	prob += (m / total) * (n / (total - 1)) * 0.5  # Aa x aa
	prob += (n / total) * (m / (total - 1)) * 0.5  # aa x Aa
	prob += (n / total) * ((n - 1) / (total - 1)) * 0  # aa x aa

	return prob


print(dominant_probability(2, 2, 2))