Day20 | Rosalind 生資解題 - 011. FIBD（Mortal Fibonacci Rabbits）限制壽命版 - 上篇

題目連結：https://rosalind.info/problems/fibd/

這一題是 004.FIB 斐波那契數列遞迴的延伸版，限制了壽命

首先來看題目

輸入

6 3

輸出

4

有了先前被嚇倒的經驗，這次出來的數字再奇葩也已經嚇不倒我了

題目意思是
在最初的第一個月只有一對小兔子，一個月後，他們會長大成熟（即，有繁殖能力）
輸入的6是回合數，3表示每一對兔子的壽命只有3個月
並且不用考慮兔子公母、奇偶數量的問題（都是以“一對”來做計算）

我們先來做簡單推演，假設兔子的壽命是：

假設兔子壽命2個月

畫一遍壽命為２個月長的兔子世代，總共８回合
日子就是：新生，老死，新生，老死...（新人馬上接替死人位置）
不斷循環，非常樸實無華

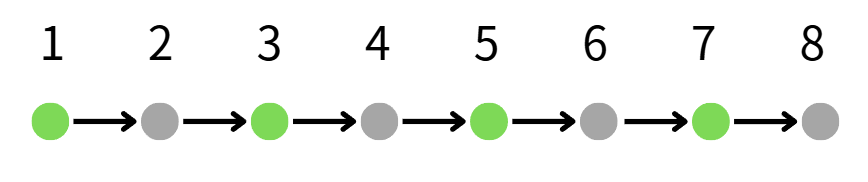
活2個月 => Fn = F(n-2) 一輩子生一對
長大到第二個月時，生出一對後，即死亡。
=> 1 1 1 1 1 1 1 1 1 1

假設兔子壽命3個月

畫一遍壽命為３個月長的兔子世代，總共８回合

一隻兔子會經歷以下的人生（兔生）

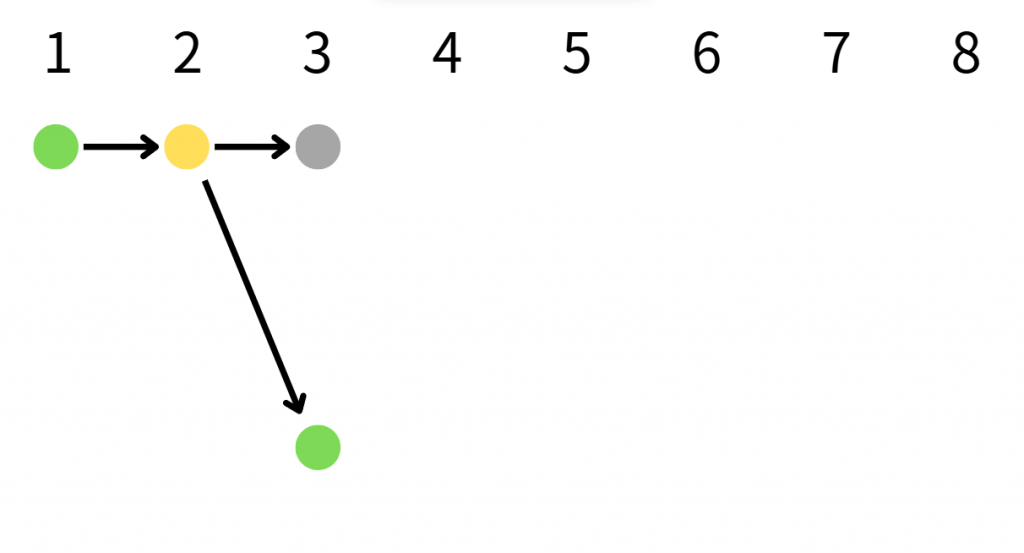
綠色代表剛出生，黃色代表成熟，灰色代表將死
黃色會生一對，灰色會生一對，但灰色下回合馬上死掉，可視作新生兒接替他的位置

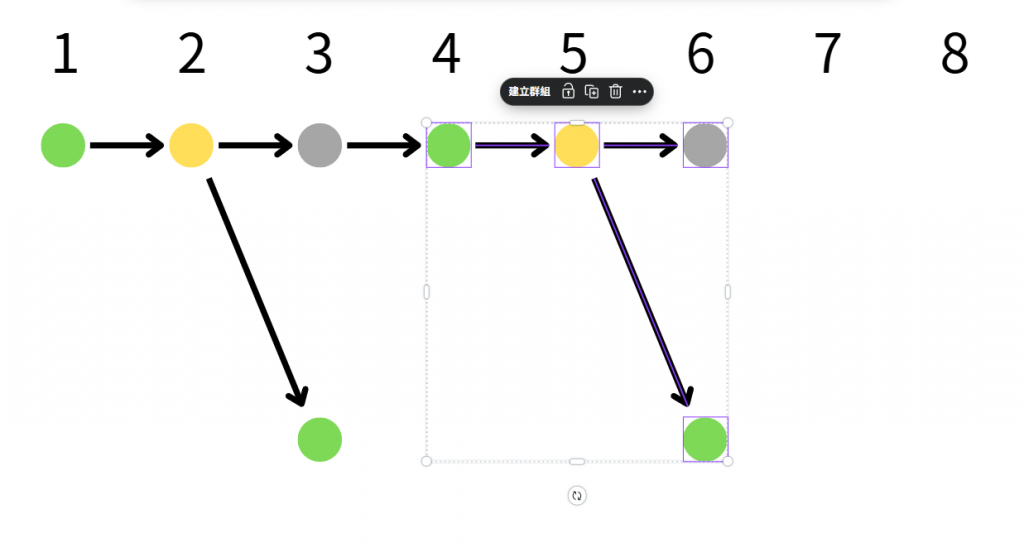
其實每一世代的兔子，都在做一樣的事情（讓我反思人類會不會也是如此啊？）

要畫出這樣的圖蠻快的，蠻推薦用Canva或小畫家之類的軟體，理一遍流程

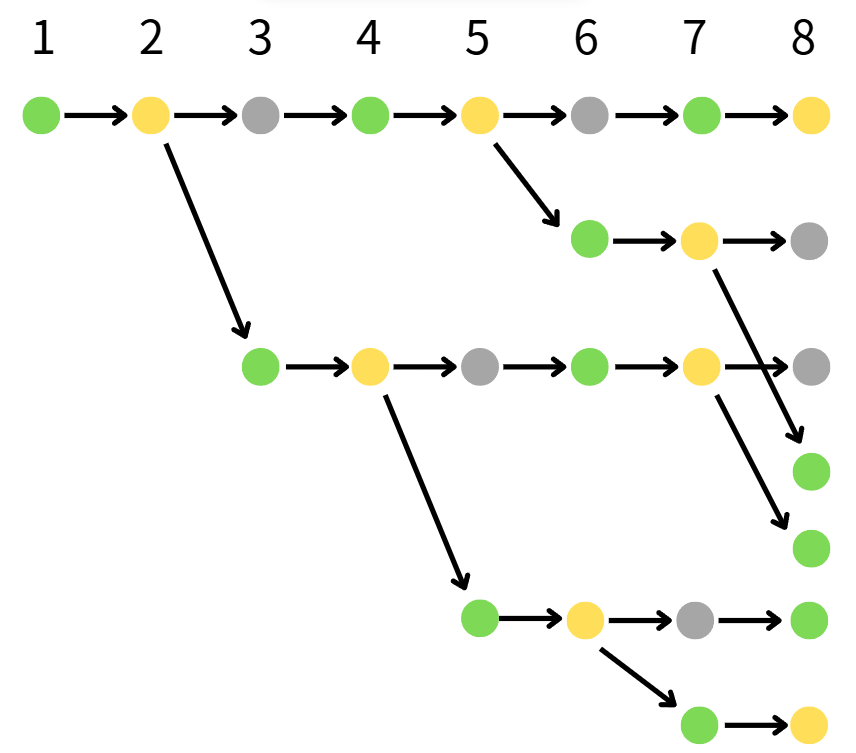
圖完成後，可以觀察出每個黃色節點（壯年期），都會分叉出一個新流程

活3個月 => Fn = F(n-2) + F(n-3) 一輩子生兩對
長大到第二個月時，生出一對，到第三個月時，再生一對，即死亡
=> 1 1 2 2 3 4 5 7 9 12

假設兔子壽命4個月

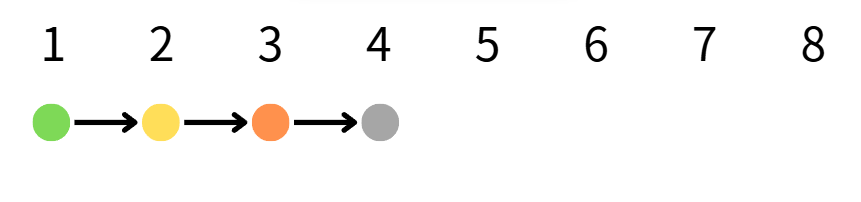
綠色代表剛出生，黃色代表成熟，橘色代表更老熟，灰色代表將死

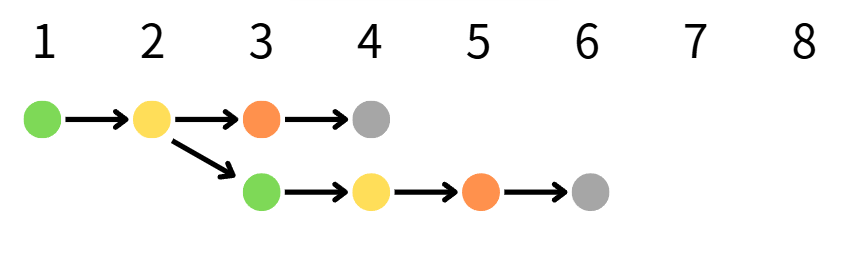
黃色節點、橘色節點，都會分叉出一個新流程

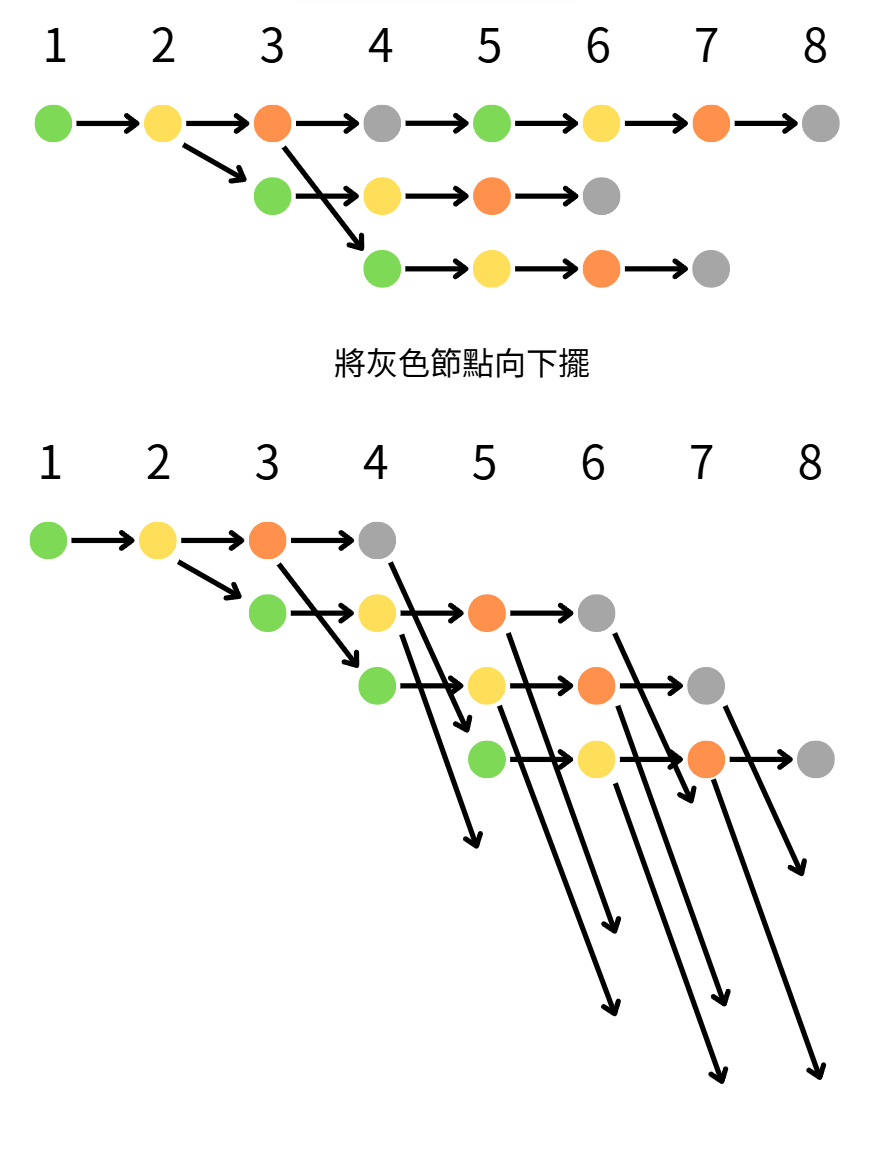
活4個月 => Fn = F(n-2) + F(n-3) + F(n-4) 一輩子生三對
第二個月時生出一對，第三個月時再生一對，第四個月再生一對，即死亡
=> 1 1 2 3 4 6 9 13 19 28

假設兔子壽命m個月

什麼，沒圖了？

（這我實在是，畫不動了...

直接上結論

活m個月 => Fn = F(n-2) + F(n-3) + F(n-4) + F(n-5) ... + F(n-m) 共m-1項
當壽命趨近於無窮時 m->∞ 則退化為經典 Fibonacci => F(n-1) + F(n-2)
=> 1 1 2 3 5 8 13 21 34 55
=> 等價於 "004_FIB" 題型，因壽命無窮不會死掉，無死亡項

有了這層"絲路"之後，便來開工寫程式碼

但是，"由簡入深易，由深入簡難"啊

當時 004. FIB 題目我們只用了兩個變數來記錄「小鼠、大鼠」，代表成熟與否。不存在年齡（死亡）問題

但這題我們要如何記錄，以明確推斷兔子的退役時間呢？
我們一步步來，一切都照著"絲路"進行
先照著題目要求，固定 n=6, m=3 假設兔子只能存活三個月

兔子只能活三個月是吧，我就用三個變數 r1、r2、r3 記錄，硬幹！
先示範錯誤的寫法：

n, m = 6, 3 # n: 回合數、m: 壽命幾個月
r1, r2, r3 = 1, 0, 0  #　個別1~m個月大的兔子數量，初始已有1對1個月大新生兔

for i in range(n - 1):  # 初始狀態已經是第1個月，所以n-1
    r1 = r2*1 + r3*1 # 這回合，新生兔子就是所有上一輪成熟兔子x1（生一對）
    r2 = r1 # 這回合2個月大兔子，就是上一輪的新生兔
    r3 = r2 # 這回合3個月大兔子，就是上一輪的2個月大兔子
    # 錯誤寫法：以上變數的更新順序有誤，覆蓋了資訊

print(r1, r2, r3) # 0 0 0

阿怎麼跑出來0 0 0死光光？
因為變數順序更新錯誤，導致資訊被覆蓋了，所以需要進行調整

正確寫法：

n, m = 6, 3 # n: 回合數、m: 壽命幾個月
r1, r2, r3 = 1, 0, 0  # 不同月份大的兔子數量

for i in range(n - 1):  # 初始狀態已經是第1個月，所以n-1
    new_born = r2*1 + r3*1
    r3 = r2
    r2 = r1
    r1 = new_born

print(r1, r2, r3) # 2 1 1

不同月份大的兔子數2 1 1，所以加起來共是4隻兔子
好的，對照答案，第一層絲路正確！

接下來要把變數r1 r2 r3的寫法改了，否則兔子活個五年我就要60個變數
這可萬萬不行
（什麼！想看我改60個變數？！你這是想看笑話吧

解法一（迭代）

多個變數 => 用「陣列」來儲存！！

n, m = 6, 3 # n: 回合數、m: 壽命幾個月
r = [0] * m # 不同月份大的兔子數量

print(r) # [0, 0, 0]
r[0] = 1 # 初始化第一隻兔子(1個月大)

for i in range(n - 1):  # 初始狀態已經是第1個月，所以n-1
    new_born = sum(r[1:]) * 1 # 這回合新生兔 = 上回合所有老兔加總
    r = [new_born] + r[:-1] # 串列於頭加入 這回合的新生兔，串列於尾部踢掉老屁股（死掉的）
    # print(sum(r))

print(sum(r)) # 4
# 迭代運算較快

寫成函式

def rabbit_population(n: int, m: int) -> int:
    """
    參數 n (int): 總月數 (共n個回合)

    參數 m (int): 壽命，兔子能活m個月
    """
    if n <= 0 or m <= 0:
        return 0

    r = [1] + [0]*(m-1)
    for _ in range(n-1):
        newborn = sum(r[1:])
        r = [newborn] + r[:-1]
    return sum(r)

print(rabbit_population(6, 3))
# 迭代運算較快

解法二（遞迴）

def born_recur(n: int, m: int) -> int:
    if n <= 0:
        return 0
    if n == 1:
        return 1
    if n <= m:
        # 還沒有死亡，等同於經典 Fibonacci
        return born_recur(n - 1, m) + born_recur(n - 2, m)


    # 以下可以簡寫成這行
    # return sum(born_recur(n - i, m) for i in range(2, m + 1))
    total = 0
    for i in range(2, m + 1):         # 計算 n-2, n-3, …, n-m 月時
        total += born_recur(n - i, m) # 那些月份的兔子在本月各生一對
    return total

print(born_recur(6, 3))  # 4
# 遞迴算法較慢


# 或者以下寫法，計算新生兔子數量

# # 計算第n回合出生的新兔數
# def births(n: int, m: int) -> int:
#     if n <= 0:
#         return 0  # 尚未進入回合
#     if n == 1:
#         return 1  # 第1回合初始條件 => 題目給定有1對新生兔
#     if n == 2:
#         return 0  # 第2回合，初代兔剛成熟，下回合才開始繁殖 ⇒ 本回合無新生
#
#     # 第3回合起：新生數 = 所有成熟兔（滿2回合以上且尚未死亡）各生 1 對
#     return sum(births(n - i, m) for i in range(2, m + 1))
#
# # 計算第n回合仍存活的兔子總數
# def alive(n: int, m: int) -> int:
#     if n <= 0: return 0
#     # 活著 = 最近m個月內出生者
#     return sum(births(n - i, m) for i in range(0, m))
#
# print(alive(6, 3))  # 4

補充數學芝士

接下來要補充一點，營養的

啊！可惜這裡的空白處太小，寫不下
要等到下一篇了...