
前面幾篇文章介紹了一些 FP 世界中的容器工具如 Functor、Monad、Applicative 等,其實還有很多沒有介紹到,例如 Reader、State 等容器,轉換容器的自然轉換(natural transformations),和重新排列型別順序的 Traversable 等,不過因為篇幅關係,這裡想先告一段落,統整目前介紹的 FP 工具以及他們和 Monoid 的關聯,最後會發現從函式到運算流程,都能以 Monoid 的方式被組合起來。
其他進一步的 FP 容器和轉換方法就有興趣的人再去了解看看囉!
很簡單的提及一點點範疇論,範疇論(Category Theory)常被視為一門高度抽象的數學分支,但對於程式設計而言,可以將其理解為「關於組合的數學」。它關心的不是事物的內部細節,而是事物之間如何關聯與組合。
在程式設計的語境下,範疇論的核心概念可以這樣對應理解:
User、Order 等型別,都是範疇中的物件。(s: string) => s.length 就是一個從 string 型別到 number 型別的態射。f: A -> B 和 g: B -> C,我們可以將它們組合成一個新的函式 h: A -> C,其定義為 h(x) = g(f(x))。範疇論的一個基本要求是,這種組合必須滿足結合律(associativity),即 (h • g) • f 與 h • (g • f) 是等價的。id: A -> A,它不做任何事,僅僅傳回輸入值。例如 const id = (x) => x。它在函式組合中的作用類似於數字 0 在加法中的角色。在程式設計世界裡,範疇論為我們提供了一套語言,讓我們能精確地描述這些關於「組合」的模式,無論組合的是數值還是整個運算流程。
在 FP 世界裡,我們會參考數學的抽象代數結構來讓程式結構更穩定、如數學般可預測。這些代數結構透過定義集合及其上的運算規則,提供了一套強大的抽象工具。以下是幾個比較常被提及的代數結構:
Magma 是最基礎的代數結構。它由一個非空集合 S 和一個定義在 S 上的二元運算 • 組成。
S 中任意兩個元素 a 和 b,其運算結果 a•b 也必須在 S 中。簡言之,只要有一組東西,以及一種能將其中任意兩個東西組合起來,並產生出同一組東西的運算,就構成了一個 Magma。這確保了運算不會產生集合之外的結果。
Semigroup 在 Magma 的基礎上,增加了一個結合律 (Associativity) 的要求。
•:同 Magma。S 中任意三個元素 a、b、c,運算的順序不影響結果,即 (a•b)•c=a•(b•c)。Semigroup 允許我們安全地「串聯」多個運算,因為無論我們如何分組,最終的結果都會相同。
Monoid 在 Semigroup 的基礎上,再增加了一個單位元素 (Identity Element) 的要求。
S 與二元運算 •:同 Semigroup。S 中存在一個特殊元素 e,對於 S 中任意元素 a,都有 a•e=a 且 e•a=a。單位元素就像一個「無作用」的元素,它在運算中不會改變其他元素的值。
Group 在 Monoid 的基礎上,再增加了一個逆元素 (Inverse Element) 的要求。
S 與二元運算 •:同 Monoid。S 中任意元素 a,都存在一個元素 $a^{-1}$,使得 $a•a^{-1}=e$ 且 $a^{-1}•a=e$ (其中 e 是單位元素)。
圖 1 逆元素示意圖(因為 iThome 無法表示 LaTeX 數學符號,只好用圖表示)(資料來源: 自行繪製)
逆元素的概念可想成是「可撤銷的操作」。對於元素 a,存在一個元素 $a^{-1}$,使得 $a•a^{-1}$ 的結果等於單位元素 $e$。
整數與加法操作就是一個 Group,對於任何整數 n,它的逆元素是 -n,因為 n + (-n) = 0(加法的單位元素)。
然而,我們常用的字串串接就不是 Group。你可以將 "Hello" 和 " World" 串接起來,但你無法輕易地「反向串接」或「撤銷」這個操作。
簡單小結這些代數結構的遞進關係:
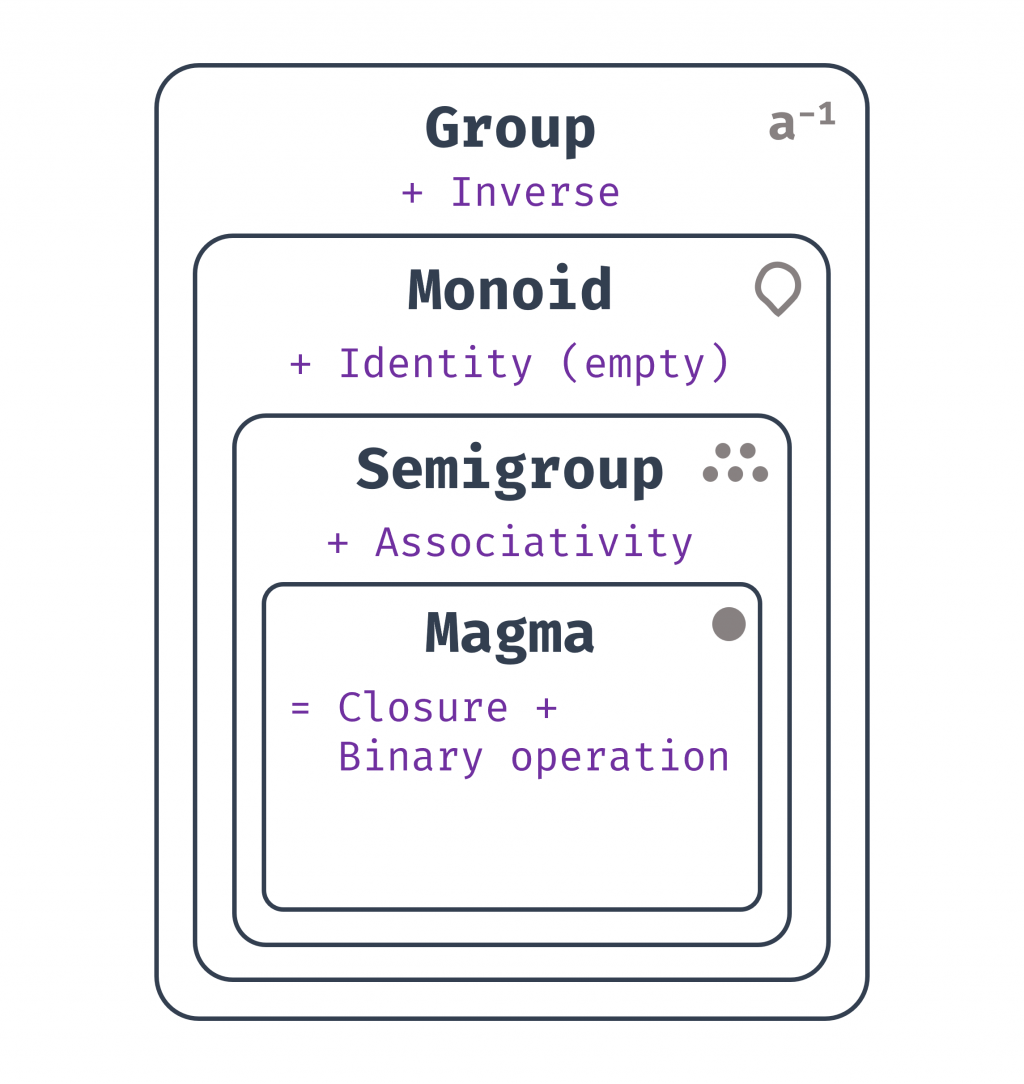
圖 2 Magma、Semigroup、Monoid 與 Group 的關係示意圖(資料來源: 自行繪製)
首先從 Semigroup 來理解,一個 Semigroup 由兩部分構成:一個集合(在程式中對應為一個型別 A),以及一個作用於該集合的二元運算(binary operation),這個運算通常被命名為 concat,其型別簽章為 concat: (A, A) -> A。這代表該運算接收兩個型別為 A 的值,經過組合後,回傳一個同樣型別為 A 的值。這個特性被稱為封閉性(closure)。
另外,這個二元運算還需滿足結合律,也就是對於任何 a、b、c,(a.concat(b)).concat(c) 的結果必須與 a.concat(b.concat(c)) 完全相同。
關於封閉性與結合律對於程式設計的意義,已在「初探 Monoid」介紹過,這裡不再贅述。
用 JavaScript 來為加法實作一個 Semigroup Sum 看看:
const Sum = x => ({
x,
concat: other => Sum(x + other.x)
});
與另一個 Sum 進行 concat,永遠會回傳一個新的 Sum:
Sum(1).concat(Sum(3)) // Sum(4)
Sum(4).concat(Sum(37)) // Sum(41)
不過要補充的是,Sum 不是「pointed functor」,因為 Sum 不能 map,Sum 只能處理 number -> number,無法轉為其他型別,且 number 並不是一個包著另一個值的容器。
再看看其他型別的 concat 方式:
// 數值相關的
const Product = x => ({ x, concat: o => Product(x * o.x) });
const Min = x => ({ x, concat: o => Min(x < o.x ? x : o.x) });
const Max = x => ({ x, concat: o => Max(x > o.x ? x : o.x) });
// 布林值
const Any = x => ({ x, concat: o => Any(x || o.x) });
const All = x => ({ x, concat: o => All(x && o.x) });
// 使用方式
Any(false).concat(Any(true)) // Any(true)
Any(false).concat(Any(false)) // Any(false)
All(false).concat(All(true)) // All(false)
All(true).concat(All(true)) // All(true)
[1,2].concat([3,4]) // [1,2,3,4]
"hello monoi".concat("d") // "hello monoid"
也可以自己寫一個簡單的 Map 的 Semigroup,並實作 concat 方法來合併物件內容,這裡的 concat 邏輯先簡單寫(相同的 key 會後蓋前),如果要每個 key 內的值都能合併,邏輯會再稍微複雜點,有興趣的可再自己實作看看。
const Map = obj => ({
obj,
concat: other => Map({ ...obj, ...other.obj }),
});
// 使用方式
Map({day: 'night'}).concat(Map({white: 'nikes'})) // Map({day: 'night', white: 'nikes'})
為何我們要為這些數值、字串或布林值定義 concat 方法呢? 用 semigroup 來思考程式有什麼用?
定義這些型別的基本元素和 concat 方法,讓我們可以統一介面,雖然他們是不同型別(數字、字串、陣列、布林、物件…),但我們都能用「組合」的思維來統一處理,而「組合」的思維有助於我們處理一些程式世界常見的模式:
用抽象的數學來思考程式,讓我們得以對介面程式設計(program to an interface),並以定律作為正確性的保證。
當容器裡的值本身是 semigroup,就能推導出整個容器也是 semigroup。
我們過去介紹的各種 Functor 如 Maybe、Either、IO 等,其實同時也能實作 Semigroup。
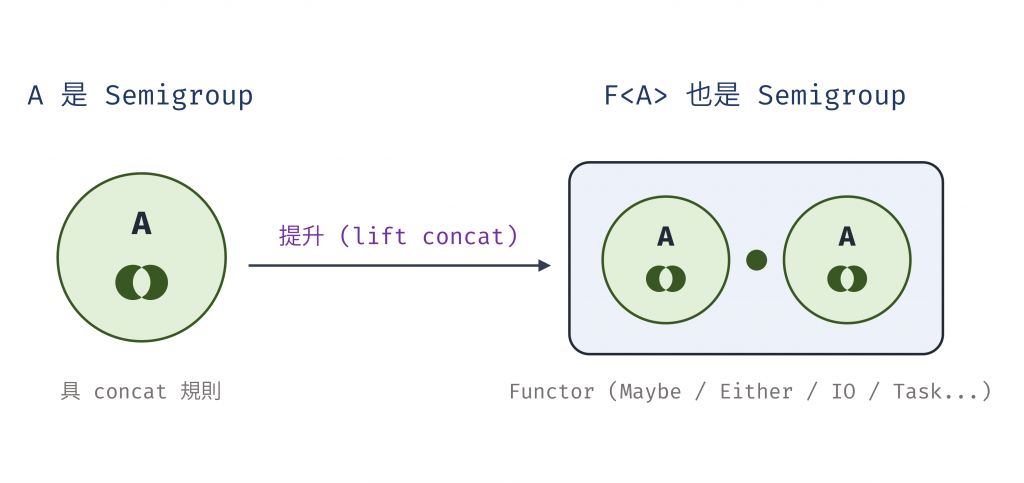
圖 3 當容器裡的值本身是 semigroup,就能推導出整個容器也是 semigroup(資料來源: 自行繪製)
舉例來說,我們可以定義 Identity 這個 Functor 的 concat 方法(Identity 就是以前所稱的 Container)。
Identity.prototype.concat = function(other) {
return new Identity(this.__value.concat(other.__value))
}
// concat 的行為:把兩個 Identity 的值合併
Identity.of(Sum(2)).concat(Identity.of(Sum(3))) // Identity(Sum(5))
Identity.of(4).concat(Identity.of(1)) // TypeError: this.__value.concat is not a function
從上範例可看出,Identity 這容器是否是 semigroup、是否可順利執行 concat,取決於 __value 是否是 semigroup。
因為 Sum(2) 有定義 .concat,所以能運作(Sum 是 semigroup),而 4 (原始數字) 沒有 .concat 方法,因此會噴錯(4 是原始數字不是 semigroup)。
由此可知,容器是否是 semigroup,取決於內部值是否是 semigroup。
Right(Sum(1)).concat(Right(Sum(4))) // Right(Sum(5))
Right(Sum(2)).concat(Left('some error')) // Left('some error')
如果組合時遇到 Right,那就正常合併,因此 Right(Sum(1)).concat(Right(Sum(4))) 的結果是 Right(Sum(5))
如果遇到 Left,就直接保留錯誤,不會繼續合併。
Task.of([1,2]).concat(Task.of([3,4])) // Task([1,2,3,4])
Task 代表非同步結果,合併時會把結果(陣列)串接起來。在定義 Task 的 concat 方法時,我們可用 semigroup 規則安全合併。
利用 semigroup 的規則,我們可以疊加不同容器,再進行組合。
// --- 底層 Semigroup:Map(其實就是物件) 與 Array ---
const SMapRHS = { concat: (a, b) => ({ ...a, ...b }) }; // 右邊覆蓋
const SArray = { concat: (a, b) => a.concat(b) };
// --- Maybe ---
const Just = (x) => ({ _tag: 'Just', value: x });
const Nothing = { _tag: 'Nothing' };
const isJust = (m) => m._tag === 'Just';
const SMaybe = (S) => ({
concat: (ma, mb) =>
isJust(ma) && isJust(mb) ? Just(S.concat(ma.value, mb.value))
: isJust(ma) ? ma
: isJust(mb) ? mb
: Nothing
});
// --- IO:包住 thunk 的容器 ---
const IO = (thunk) => ({
run: thunk,
map: (f) => IO(() => f(thunk())),
});
const SIO = (S) => ({
concat: (ia, ib) => IO(() => S.concat(ia.run(), ib.run()))
});
// --- Task:這裡用 Promise 當 Task ---
const Task = (thunk) => ({
run: () => thunk(),
map: (f) => Task(() => Promise.resolve(thunk()).then(f)),
});
const STask = (S) => ({
concat: (ta, tb) => Task(async () => S.concat(await ta.run(), await tb.run()))
});
// -------------------- 範例開始 --------------------
// 範例 1:IO(Either(Map)):讀表單資料 → 驗證
// 「先驗證,再合併」,Left 直接傳遞
const Right = (x) => ({ _tag: 'Right', right: x });
const Left = (e) => ({ _tag: 'Left', left: e });
const isRight = (e) => e._tag === 'Right';
const SEither = (S) => ({
concat: (ea, eb) =>
isRight(ea) && isRight(eb)
? Right(S.concat(ea.right, eb.right)) // 兩個 Right 才合併
: isRight(ea)
? eb // 左邊 Right、右邊 Left -> 回 Left(短路)
: ea // 左邊 Left -> 回 Left(短路)
});
// formValues :: Selector -> IO(Map)
const formValues = (sel) =>
IO(() => (sel === '#signup'
? { username: 'andre3000' }
: sel === '#terms'
? { accepted: true }
: {}));
// validate :: Map -> Either Error Map
const validate = (m) =>
m.accepted === false ? Left('must accept terms') : Right(m);
// IO(Either(Map)) 的 semigroup:由內部 Map 的合併規則一路提升
const SIOEitherMap = SIO(SEither(SMapRHS));
// OK:兩個表單都驗證成功 → 內部 Map 合併
const ok = SIOEitherMap.concat(
formValues('#signup').map(validate),
formValues('#terms').map(validate)
).run();
// => Right({ username:'andre3000', accepted:true })
// BAD:其中一邊變成 Left → Left 直通
const bad = SIOEitherMap.concat(
formValues('#signup').map(validate),
IO(() => Left('one must accept our totalitarian agreement'))
).run();
// => Left('one must accept our totalitarian agreement')
console.log(ok, bad);
// 範例 2:Task(Array):兩個非同步請求並行 → 結果用陣列 semigroup 合併
const serverA = { get: () => Task(() => Promise.resolve(['friend1'])) };
const serverB = { get: () => Task(() => Promise.resolve(['friend2'])) };
const STaskArray = STask(SArray);
STaskArray.concat(serverA.get('/friends'), serverB.get('/friends'))
.run().then(console.log);
// => ['friend1','friend2']
// 範例 3:Task(Maybe(Map)):載入兩組設定(可能有缺)
//(有的才合、沒有就跳過)
const loadSetting = (key) => Task(async () => {
if (key === 'email') return Just({ backgroundColor: true });
if (key === 'general') return Just({ autoSave: false });
return Nothing;
});
const STaskMaybeMap = STask(SMaybe(SMapRHS));
STaskMaybeMap.concat(loadSetting('email'), loadSetting('general'))
.run().then(console.log);
// => Just({ backgroundColor:true, autoSave:false })
以上程式有三個組合的範例:
IO(Either(Map)) 會讀取表單資料,再驗證,然後合併結果,如果成功就順利組合,失敗就短路回傳錯誤訊息Task(Array) 會從兩個伺服器抓朋友清單,再合併成一個結果Task(Maybe(Map)) 會載入多個設定檔並合併雖然這些也可以用 chain 或 ap 來組合,但用 semigroup 來思考會更簡潔。
由此可知,不同層的容器可以疊加,因為底層值本身都是 semigroup。
如果一個資料結構的每個欄位本身都是 semigroup,那整個資料結構也自然構成 semigroup。如果我們能 concat 零件,就能 concat 整體。
假設有個 UserStats 資料結構,裡面有 posts 貼文數量、tags 使用過的標籤和 longestSession 最長連續使用時間這三個欄位,且這三個欄位各自都是 semigroup,那 UserStats 本身也成為一個 semigroup,UserStats 本身也可以 concat。
// 底層 semigroups
const Sum = (x) => ({
x,
concat: (other) => Sum(x + other.x),
toString: () => `Sum(${x})`
});
const Max = (x) => ({
x,
concat: (other) => Max(Math.max(x, other.x)),
toString: () => `Max(${x})`
});
// UserStats 資料結構
const UserStats = (posts, tags, longestSession) => ({
posts, // Sum
tags, // Array
longestSession, // Max
concat: (other) =>
UserStats(
posts.concat(other.posts),
tags.concat(other.tags),
longestSession.concat(other.longestSession)
)
});
// 測試
const stats1 = UserStats(Sum(5), ['fp', 'monoid'], Max(120));
const stats2 = UserStats(Sum(3), ['functor'], Max(90));
const combined = stats1.concat(stats2);
console.log(combined);
// UserStats { posts: Sum(8), tags: ['fp','monoid','functor'], longestSession: Max(120) }
假設我們定義一個事件流的型別 Stream,這個事件流可以想像成一個持續不斷、隨時間發生變化的資料流,其中的每一筆資料都代表一個發生的事件,例如使用者點擊、IoT 裝置回報的感測器讀數、金融交易紀錄等。
在前端應用中,常見的事件流處理函式庫例如 RxJS,RxJS 會在之後介紹,這裡想說明的是,事件流 Stream 也是可以透過 concat 聚合的。而 RxJS 組合事件流的概念也與此有關。
const $ = (sel) => document.querySelector(sel);
// 來源:click 與 Enter
const submitStream = Stream.fromEvent('click', $('#submit'));
const enterStream = Stream.fromEvent('keydown', $('#myForm'))
.filter(e => e.key === 'Enter');
// 合併來源 → 統一處理
const submitFlow =
submitStream
.concat(enterStream) // ⬅️ 合併事件流
.map(e => {
e.preventDefault(); // 避免表單跳頁
return $('#username').value; // 當下 input 的值
})
.map(submitForm); // 提交表單的處理邏輯
我們定義了 click 事件觸發的事件流 submitStream,以及 enter 按鍵觸發的事件流 enterStream,然後透過 concat 將事件流合併,這樣不論是 click 觸發的事件還是 enter 觸發的事件,都會匯聚在一起,並執行提交表單的處理邏輯。
這裡聚焦在容器型別 Stream 的 concat 範例,如何 subscribe 事件流來讓整體可運作,就先不細部解說,會在 RxJS 篇章再來說明~不過還是補上可運行的程式範例連結,有興趣的可參考看看。
從上面範例可看出,我們可以把事件串流合併成新的串流,不過合併的前提是,事件串流的內部值也要是 semigroup,這樣才能順利合併內容。
每個型別可以定義不同的合併方式,舉例來說,Task 的合併方式可以是:
具體的合併方式,就依照實際應用的需求來決定。如果想更了解如何選擇合併方式,可再看看 Alternative interface,它實作了一些方案,重點聚焦於「選擇」而不是「層疊組合」。(附上 fp-ts 的Alternative 型別連結)
雖然 Semigroup 提供了組合的方式,但在某些情況下,它還有些不足,假設有個聚合操作,例如加總一個數字列表。如果列表是 [1, 2, 3],我們可以輕易地使用 Semigroup Sum 來得到 6。但如果列表是空的 [] 呢?Semigroup 並沒有告訴我們如何處理這種「無物可合」的情況。這正是 Monoid 登場的時機,也是我們熟悉的單位元素出場的時候。
在「初探 Monoid」的文章中已經介紹過什麼是 Monoid,不過了解 Semigroup 後,再看一次 Monoid 定義會更了解其意義:
一個 Monoid 就是一個帶有「單位元素 (Identity Element)」的 Semigroup。
這個單位元素通常稱為 empty,它必須遵守兩條定律:
empty.concat(a) 的結果必須等於 a
a.concat(empty) 的結果必須等於 a
簡單來說,單位元素就是一個在組合操作中「什麼都不做」的值。它提供了一個安全的起始點。
Array.empty = () => []
String.empty = () => ""
Sum.empty = () => Sum(0)
Product.empty = () => Product(1)
Min.empty = () => Min(Infinity)
Max.empty = () => Max(-Infinity)
All.empty = () => All(true)
Any.empty = () => Any(false)
單位元素對程式設計的意義已經在初探 Monoid說明過,這裡不再重複。
fold:有預設值的 reduce初探 Monoid 文章有提到,reduce 方法可說是 Monoid 模式的完美體現,二元運算函數對應到 concat,初始值則對應到 empty。而如果我們沒有給 reduce 初始值 initialValue 的話,就會出現錯誤,由此也可看出單位元素的重要性。
為了讓 reduce 能更安全的被使用,可定義一個安全版的 reduce,強制一定要傳入初始值(即 Monoid 的 empty),這個安全版的 reduce 可命名為 fold:
// reduce :: (b -> a -> b) -> b -> [a] -> b
// fold :: Monoid m => m -> [m] -> m
const fold = reduce(concat)
fold 接收一個 Monoid 的 empty 作為初始值(初始的 m),然後再壓縮一個 Monoid 陣列 [m] 得到最後的值,這樣做的好處是,即使陣列是空的,也能安全回傳單位元素。
fold 的使用範例以下看一些 fold 的使用範例~
fold(Sum.empty(), [Sum(2), Sum(1)]) // Sum(3)
fold(Sum.empty(), []) // Sum(0)
fold(Any.empty(), [Any(false), Any(true)]) // Any(true)
fold(Any.empty(), []) // Any(false)
fold(Either.of(Max.empty()), [Right(Max(3)), Right(Max(21)), Right(Max(11))])
// Right(Max(21))
fold(Either.of(Max.empty()), [Right(Max(3)), Left('error retrieving value'), Right(Max(11))])
// Left('error retrieving value')
在 Either 的範例中,可看到如果是 reduce 所有 Right,最後會取最大值 Right(Max(21)),但如果中間有 Left,就會直接傳遞錯誤,不繼續合併。
有些 Semigroup 無法定義一個合理的 empty 值,例如 First 這個型別:
const First = x => ({
x,
concat: other => First(x)
})
First(x) 的意思是保留第一個值,不管後面 concat 什麼,都回傳最初的那個。
實際應用的情境例如為一筆新資料定義 id,不管後面如何整合,都不該覆蓋或合併掉原先定義的 id 值。First 的整合範例如下。
Map({
id: First(123),
isPaid: Any(true),
points: Sum(13)
}).concat(
Map({
id: First(2241),
isPaid: Any(false),
points: Sum(1)
})
)
// 結果: Map({id: First(123), isPaid: Any(true), points: Sum(14)})
由上可知,對於 id 欄位,First(123) 和 First(2241) 整合後只會得到第一個值 First(123)。
而 First 是無法有 empty 元素的,可以想想看,如果要定義 First.empty(),應該回傳什麼?
這沒有合理答案,因為「第一個值」必須來自實際資料,不可能從空值開始。
並非所有 Semigroup 都能成為 Monoid,但這並不代表這種 Semigroup 沒有用,因為在實務上仍有應用情境,例如 First 可用在使用者註冊時的原始 ID 值,或用在處理設定檔的合併,當遇到多個 config 檔案時,First 代表「不論後面的設定是什麼,永遠取第一個載入的值」。
目前為止,我們已經看到 Monoid 如何組合資料:數字相加 (Sum)、布林值判斷 (All)、甚至合併整個 UserStats 物件。我們也看到,只要容器內的值是 Monoid,整個容器 F<Monoid> 也能成為 Monoid。
我們討論了很多「組合」,那「組合」這個行為本身,是否也能形成一個 Monoid 呢?
可以,而這正是 Monoid 如此強大的原因,它不僅僅是關於資料的模式,更是關於運算與行為的模式。接下來會看到,FP 世界中核心的三個概念——函式組合、Monad 和 Applicative——其本質都可以用 Monoid 來詮釋。
函數式程式設計最基礎的運算就是函式組合,來看看為何 g(f(x)) 這樣的程式碼可滿足 Monoid 的定義。
a -> a。例如 (x: number) => x + 1。concat):運算就是 compose 函式。compose(g, f) 會回傳一個新的函式 x->g(f(x))。這個新函式依然是一個 a -> a 的 Endomorphism,滿足封閉性。empty):單位元素是 id 函式,const id = x => x。可建立一個名為 Endo 的 monoid:
const Endo = run => ({
run,
concat: other =>
Endo(compose(run, other.run))
})
Endo.empty = () => Endo(identity)
Endo:包裝一個函數 run
concat:透過 compose 來組合兩個函數(維持輸入輸出型別一致),因為它們都是相同的型別,所以可以用 compose 來 concat,且型別總是對得上(上一個的輸出型別與下一個需要的輸入型別相同)Endo.empty():單位元就是恆等函數 (identity)使用範例如下:
// thingDownFlipAndReverse :: Endo [String] -> [String]
const thingDownFlipAndReverse = fold(
Endo(() => []),
[Endo(reverse), Endo(sort), Endo(append('thing down'))]
)
thingDownFlipAndReverse.run(['let me work it', 'is it worth it?'])
// ['thing down', 'let me work it', 'is it worth it?']
這程式建立了一個 fold 函式,將多個 Endo 函數依序組合(compose):
reverse:反轉陣列sort:排序陣列append('thing down'):在陣列後面加上 'thing down'
並且設立初始值 Endo(() => []),若沒有元素,回傳空陣列,最後執行時,compose 會由右到左執行,先 append('thing down') 再排序,最後反轉,輸出新字串陣列。
compose(h, compose(g, f)) 等於 compose(compose(h, g), f)。結合律成立。compose(f, id) 結果等於 f,compose(id, f) 結果等於 f。單位律成立。滿足所有定律,因此可以將函式組合定義為一個 Monoid。
我們之所以能夠安心地建立函式處理管線 (pipeline),並隨意重構 h(g(f(x))) 這樣的程式碼,其背後的數學保證正是 Monoid 定律。
「Monad is a Monoid in the Category of Endofunctors」這句話的解釋在之前 [Day 22] Monad 入門 (2):核心概念與定律 有提到過,今天更認識 Endofunctors 後,再來看看這是什麼意思,也許會有不同的理解。
我們可分兩種層次的理解方式,第一種從程式設計角度的「串接運算」出發,第二種則回歸更根本的範疇論定義。
Monad 為那些「回傳 Monad 的函式」提供了一種符合 Monoid 定律的組合方式。
回想一下我們在 Monad 文章中學到的 chain (或 flatMap)。它的作用就是將一個 M(a) 和一個運算函式 a->M(b) 組合起來。這類 A → M(b) 形式的函式,代表著「接收一個普通值,回傳一個帶有上下文(如 Maybe、Task)的值」,它們被稱為 Kleisli arrow。
Monad 的本質,就是定義如何組合這些 Kleisli arrows。
A->M(B) 形式的函式。compose,稱為 kleisliCompose (在 Haskell 中是 >=>)。它接收兩個 Kleisli arrows,f:A->M(B) 和 g:B->M(C),並將它們組合成一個新的 Kleisli arrow h:A->M(C)。這個組合的內部實現就是 chain。of (或 pure, return) 函式,型別是 A->M(A)。Monad 的三條定律,正是 Monoid 定律在 Kleisli arrow 組合這個情境下的具體體現。
kleisliCompose(h, kleisliCompose(g, f)) 等於 kleisliCompose(kleisliCompose(h, g), f)。對應到 Monad 的結合律意思就是 (m.chain(f)).chain(g) 等於 m.chain(x => f(x).chain(g))。kleisliCompose(f, of) 和 kleisliCompose(of, f) 都等於 f。這對應到 Monad 的左右單位律。Monad 將 Monoid 這個強大的組合模式,應用於帶有上下文的運算流程中。當我們寫下 getUser(id).chain(getPostsByUser) 時,我們真正在做的不是在合併兩個 Task 值,而是在合併兩個「產生 Task 的動作」。
Monad 提供了一個符合 Monoid 定律的、安全可靠的方式來串聯這些動作。
如果以範疇論視角來看 Monad,可看一下在 Endofunctors 這個特殊範疇內的元素:(一個 Endofunctor 指的是像 Maybe 或 Array 這樣,能將一個型別 A 包裹成 F(A),且兩者都存在於同一個型別系統中的 Functor)。
forall a. F(a) -> G(a) 的函式,它能在不改變內部值的結構下,轉換容器的型別。來看看 Monoid 如何在這個「Endofunctors 範疇」中定義:
join 。它是一個自然轉換,型別為 M(M(A)) → M(A)。它的作用是將兩層巢狀的 Monad 壓平成一層。of 或 return。它也是一個自然轉換,型別為 A → M(A) (更精確地說是從 Identity functor 轉換)。它的作用是將一個普通值放入 Monad 這個「單位容器」中。這兩種視角是完全等價的,因為 chain (或 bind) 和 join 可以互相定義:
m.chain(f) 等價於 join(map(f, m))
join(m) 等價於 m.chain(id)
Monad 的定律無論是用 chain 還是 join 來理解,最終都指向 Monoid 的結合律與單位律,因此可將 Monad 定義為一個 Monoid (並且是 Endofunctors 範疇中 Monoid)。
補充:Endomorphism 與 Endofunctors 差異
1. Endomorphism (自態射 / 自函式)
- 層級:值的世界 (World of Values)
- 定義:一個輸入型別與輸出型別完全相同的函式。
- 簽章:
A -> A- Endomorphism 描述的是「同型別的值之間的轉換」。它接收一個值,經過運算後,回傳一個相同型別的值。
- 範例:
const increment = (x: number): number => x + 1;- 恆等函式 id 也是一個典型的 Endomorphism。
- 當我們討論函式組合的 Monoid 時,我們組合的正是這些
A -> A的 Endomorphism。2. Endofunctor (自函子)
- 層級:型別的世界 (World of Types)
- 定義:一個將一個範疇 (Category) 映射回自身的 Functor。
- 概念:在程式設計中,這通常指一個容器或結構,它能接收任何型別
A,並將其包裹成一個新的型別F<A>,而F<A>依然存在於我們原有的型別系統中。- Endofunctor 描述的是「將型別提升到一個結構中」的模式。
- 範例:以 Maybe 來說,你給它
String型別,它產生Maybe<String>型別。
| 特性 | Endomorphism | Endofunctor |
|---|---|---|
| 操作對象 | 值 (Values) | 型別 (Types) |
| 本質 | 是一個函式 | 是一個結構/容器 |
| 簽章/模式 | A -> A |
A => F<A> |
| 簡單來說 | 值的同型別轉換 | 型別的結構化包裹 |
| 比喻 | 一台「將木頭加工成木椅」的機器 | 一份「為任何材料設計容器」的藍圖 |
Applicative Functor 之所以能夠「同時」處理多個獨立的計算、再把結果合併,其實背後的關鍵結構就是 Monoid。
這個特性在範疇論中被稱為 Lax Monoidal Functor —— 意即一種「能以 Monoid 方式結合的 Functor」。
我們可以從兩個角度來看這件事:
Applicative 的核心在於它能將兩個獨立的容器「並行」地組合起來,變成一個新的容器。為了更清楚表達這個「並行結合」的概念,我們可以定義一個比 ap 更基礎的操作,稱為 product (或 zip)。
// product :: (F(A), F(B)) -> F((A, B))
這個操作接受兩個容器,並將它們組合成一個裝有 tuple 的新容器。例如以下:
product([1, 2], [3, 4])
// => [[1, 3], [1, 4], [2, 3], [2, 4]]
它做的事其實就像是「容器的 concat」,只不過是「同時」結合兩個容器裡的值。這裡就是對應到之前 [Day 24] Applicative Functor (2):定律與應用範例提到的笛卡兒積的概念。
這操作對應到 Monoid 的結構來看:
F(A),其中 F 是一個 Applicative。product): (F(A), F(B)) -> F((A, B))。此操作接收兩個容器,回傳一個新的容器,裡面裝著包含原先兩個值的元組 (tuple)。of(()),一個包裹著「空元組」或「單位值」的容器。product 操作就是 Applicative 的 monoidal concat。一旦有了 product,我們就可以用它和 map 來重新定義出 ap:
// ap :: Functor f => (f (a -> b), f a) -> f b
const ap = (fab, fa) =>
map(
([f, a]) => f(a), // 對「裝著 pair」的容器做 map:把每個 pair 解構成 f 與 a,再呼叫 f(a),最後把結果留在原本的容器語境中
product(fab, fa) // 先把兩個容器並行結合,得到一個新容器,裡面放著 pair/tuple:[(函式), (值)]
)
由此可看出 ap 的本質,ap 其實是由一個「Monoid 式的結合 (product)」再加上一個「函數式轉換 (map)」組成的。
這也就是為什麼 Applicative 能自然地組合多個獨立的運算,例如:將多個異步結果合併成單一結果,因為它本質上就是「Monoid 化」的結合邏輯。
前面說的是 Applicative 本身具備 Monoid 結構。
接著我們要看另一種情況:
當一個 Applicative Functor 內部包裹的值本身就是 Monoid 時,整個結構
Applicative<Monoid>也會成為一個 Monoid。
concat 提升到 ApplicativeMaybe、Promise 或 Task,裡面包著 Monoid 值(例如字串或陣列):Maybe("Hello ")
Maybe("World")
字串本身有 Monoid 結構,concat 為字串拼接,empty 為空字串 ""。
那麼我們就可以用 liftA2 來「提升」字串的 concat,讓它能作用在 Applicative 上:
const concatA = liftA2((a, b) => a.concat(b))
concatA(Maybe("Hello "), Maybe("World"))
// => Maybe("Hello World")
liftA2 的作用就是把一個普通的二元函數(這裡是 Monoid 的 concat)提升成「Applicative-aware」的版本。也就是說,它會自動幫我們拆開兩個容器、取出裡面的值、套用函數、再包回容器中。以這裡來說,就是 liftA2 拆開了兩個 Maybe 容器,取出裡面的字串,套用字串的 concat 函數,再把結果包回 Maybe 容器中。
empty 也能被提升F.of(M.empty)
舉例來說:
Maybe.of("")
Promise.resolve([])
Task.of(0)
這樣 Applicative<Monoid> 整體就成為一個新的 Monoid:
concat: 透過 liftA2 來結合內部值,liftA2 接收一個普通的二元函式(在此就是內部 Monoid 的 concat),並用它來合併兩個 Applicative 容器內的值。empty: 單位元素就是內部 Monoid 的 empty 值,被 of 方法提升到 Applicative 的上下文中:F.of(M.empty)。我們從 Semigroup 出發,一路深入到 Monoid 在函式組合、Monad 和 Applicative 中的應用,最後發現 Monoid 將一切都串連起來了。
以下是本文的重點摘要:
compose 是 concat,id 函式是 empty。我們使用的函式組合,其穩定性正源於 Monoid 定律。chain 和 of 遵循 Monoid 定律,為帶有上下文(如錯誤處理、異步)的運算提供了可靠的串聯方式。從更根本的角度看,Monad 本身就是 Endofunctor 範疇中的一個 Monoid,其中 join 是組合操作,of 是單位元素。ap 操作可以從一個更根本的 product 操作(將兩個容器合併為一個內含元組的容器)推導而來,這揭示了其內在的 Monoid 特性。最終我們發現,從 Functor、Applicative 到 Monad,這些看似獨立的概念,最終都可透過 Monoid 的視角被統一和理解。它顯示了函數式程式設計的核心——萬物皆可組合。
一開始讀 FP 相關文章的時候我會覺得這些數學理論、結構很令人頭痛,其實現在也不能說完全理解這些數學,但我覺得以程式設計的角度來看,FP 程式設計的思維只是想去借用數學的理論,例如程式設計中,沒有副作用的純函數就是去參考數學的「函數」,每一個輸入值,都只會對應到一個確切的輸出值,有了純函數的前提,我們又可以進一步去借鏡這些數學的代數結構,參考結合律、單位元素,讓一切變得可隨意組合和拆解,當程式能安全地隨意組合和拆解,開發上就能有更大的彈性,例如可實踐分層設計、分而治之等模式。
也因此我覺得我們只需大概理解背後的數學理論概念即可,雖然我覺得讀這些數學結構也蠻有趣的...有時間的話還是想深入探索 XD
不過回到程式設計本身,重點是這些數學理論能幫助我們解決什麼問題、如何確保我們複雜的程式開發是穩定可預測的。接下來的文章會介紹實務開發上,哪些技術和 FP 有關,也許會發現 FP 概念處處可見~
如果對代數結構(Algebraic Data Type)有興趣的,可參考以下這些連結,我覺得都寫得很好!

這篇超多字,講得很細,來表示一下敬佩之意。 <O>
感謝大大~! taiansu 大大的FP文章也是之前讀 FP 的參考資源之一🙏