# 建立決策樹（Decision Tree）

[決策樹圖]
決策樹是一種非常直覺且容易理解的分析模型，樹上的每個節點（node）代表資料的分類依據，資料通過節點後會依其屬性被分到不同的分支（branch）上，最後得到該資料所屬的分類。

# 決定分支的方法：Information entropy

在建立決策樹時最大的問題就是：如何決定節點該用什麼屬性（attribute）來作為分支依據？
例如我們想要判斷某一天是否適合外出遊玩，我們可能會考慮到這天的屬性：天氣、濕度、溫度及有沒有風這四個屬性。

我們當然可以很直覺得把四個屬性的決策分支都畫出來，然後憑直覺挑一個 XD
通過直覺選擇出來的決策樹也許有不低的精准度，但這樣的方法肯定不靠譜，因此各種科學家們想出了一個度量法來客觀地決定分支的依據，這個方法被稱為 informaiton entropy （資訊熵 :o ）。

# 決定分支依據

假設我們有資料長這樣，我們想建立 Play 的決策樹（資料是書裡的，Weka 裡也有，應該可以拿來用吧...）

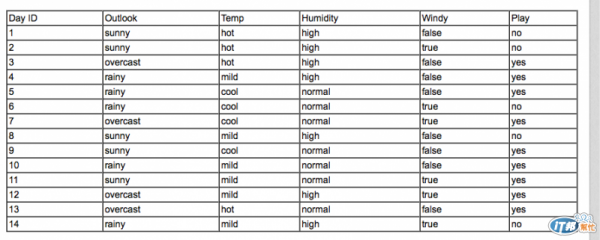
決策樹最開始，先決定 root node（第一個分支點）該使用什麼屬性，流程如下：
先算出各分支的 information 值（例如 outlook 可以分出三支，即 sunny, overcast 和 rainy，要算出 info(sunny), info(overcast), info(rainy) ）
算出分支的總 information，即 info(sunny, overcast, rainy)，算法後面介紹
算出主幹的 information（即 info(outlook)）
將 info(主幹) - info(分支總) 得到 gain(屬性)
把最後得到的 gain(屬性) 拿去跟其他的屬性的 gain 值相比，最大者就是我們理想的分支依據
我們拿 outlook 做範例，他的分支情形如下表示（ps. [2,3] 表 [yes, no] 的數量分佈）

outlook(sunny=[2,3], overcast=[4,0], rainy=[3,2])

1. 計算各分支 info
   info(sunny) = info([2,3]) = 0.971 bits （information 用 bits 做單位）
   info(overcast) = info([4,0]) = 0.0 bits
   info(rainy) = info([3,2]) = 0.971 bits

2. 算出分支總 info
   info(sunny, overcast, rainy)
   = info([2,3], [4,0], [3,2])
   = 5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971
   = 0.693 bits

3. 算出主幹 info
   info(outlook) = info([9,5]) = 0.940 bits

4. 算出主幹屬性分數 gain
   gain(outlook)
   = info(outlook) - info(sunny, overcast, rainy)
   = info([9,5]) - info([2,3], [4,0], [3,2])
   = 0.940 - 0.693
   = 0.247 bits

gain(outlook) = 0.247 bits 我們這邊就簡單看成以 outlook 做分支時，它所含的資訊量，數值越高代表資訊含量越多（詳細的涵義請自行 google ...）。

以上述步驟類推其他屬性的 gain 值：
gain(temperature) = 0.029 bits
gain(humidity) = 0.152 bits
gain(windy) = 0.048 bits

當我們完成以不同屬性做分支所含的資訊量，我們便可以選出資訊含量最高的，即 gain 值最高的，作為我們分支的屬性，在這個範例中，很明顯 gain(outlook) 的資訊含量最高，因此我們取 outlook 作為我們的第一個分支節點的屬性依據。

其他的節點也可以依據此法個別處理，當資料無法再做更多的分支，或者分支的資料都屬於相同的屬性時，我們的決策樹就完成了。

(to be continued...)