# information entropy 要怎麼算？

基本的公式在此：

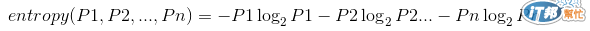
ps.1 Pn 表示 個別分類結果的占總數量有多少
ps.2 通常 log 以 2 為底

ex. info([2,3,4]) = entropy(2/9, 3/9, 4/9) = -2/9 x log(2/9) - 3/9 x log(3/9) - 4/9 x log(4/9)
關於這個的原理什麼的，自己去 Google 吧（數學苦手表示難過 Orz）

而計算分支總 info = 個別 info 乘上個別所占的比例（有點像期望值 :o）
info([2,3], [4,0], [3,2]) = (5/14) x info([2,3]) + (4/14) x info([4,0]) + (5/14) x info([3,2])

information entropy 的計算上有三個性質：

1. 如果有分類結果為 0 的，info 值就會是 0。例如上面的 info([4,0]) = 0 bits
2. 分類結果數量相等時，info 會有最大值
3. multistage property

前面兩個應該很好懂，至於什麼是 multistage property 勒？
簡單來說就是，分類這回事其實是可以層層進行的。
例如我們有個分類結果為 [2,3,4]，被分成三個類別，當我們在分類的時候其實可以看成兩個步驟
第一次分類 [2,7]
第二次分類 [2,3,4]
於是我們計算 info([2,3,4]) 時，事實上是在做這個運算：
info([2,3,4]) = info(2,7) + (7/9) x info([3,4])
為什麼會這樣？？改天再說吧......

真的在計算的時候拿 log 那個公式做就好了 :p

當樹的分支太細碎時：Gain Ratio

information entropy 提供了我們一個客觀的標準來決定決策樹的分支屬性，然而他有一個缺點，就是在分支的屬性造成太多分支時，我們會得到一個合理但卻讓決策樹的分類產生問題的結果。
假設我們拿上面資料的 Day ID 作為節點分支的依據，會產生高達 14 個分支，我們計算個別分支的總 info 值時，會得到 0：

info([0,1]) + info([0,1]) + info([1,0]) + ... + info([0,1]) = 0

這時的 gain(Day ID) 就會等於 info([9,5]) = 0.940 bits
（ gain(root) = info(root) - info(branches) and info(branches) is 0 now ）

gain(Day ID) 非常大，遠大過於先前計算的四個屬性的 gain 值，這樣的話我們是不是應該拿 Day ID 作為節點的分類依據呢？很明顯如果我們拿了 Day ID 作為分類的依據，當有一個未知的新資料要做分類時，就會造成分類上的問題。

這時我們就會需要 gain ratio 的概念，簡單來說就是把分支的數量也加入考慮，使我們在選取分類依據時能更加的準確客觀。
以 Day ID 做依據時，總共會產生 14 個分支，每個分支下僅有一個分類，則這個分支的 info 值為
info([1,1,1,1,...,1]) = -1/14 x log(1/14) x 14 = 3.807 bits
因為分支的數量相當多，所以他的 info 值也相當的大。

接著我們就可以求出 gain ratio ，直接把原本的 info 值除以分支數量的 info 值：
0.940 / 3.807 = 0.247

試著計算 outlook 分支數量的 info：
info([5,4,5]) = 1.577 （分支數量為 5,4,5）
這時可得 outlook 的 gain ratio
0.247 / 1.577 = 0.156

在這個範例中，Day ID 的 gain ratio 仍然高於其他四個屬性的 gain ratio，但他們的差距已經小很多，在實際的應用上我們可以透過隨機測試 （ad hoc test，請參考下方連結）來剔除那些沒用的屬性，換句話說就是要多多嘗試啦，不要相信單一的結果...

決策樹相關研究

John Ross Quinlan 是一位在決策樹的演算法上有相當成果的一位科學家，他發明了一些很有名的算法像是 ID3, C4.5 等，有興趣的人可以自己去查查看 ...
附上 C4.5 algorithm 的聯結
http://en.wikipedia.org/wiki/C4.5_algorithm

References

[資訊的度量 - Information Entropy](http://blog.xuite.net/metafun/life/69851478-%E8%B3%87%E8%A8%8A%E7%9A%84%E5%BA%A6%E9%87%8F-+Information+Entropy)
[Entropy](http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/)
[information entropy 在 wiki 上的介紹](http://en.wikipedia.org/wiki/Entropy_%28information_theory%29)
[ad hoc test](http://blog.csdn.net/wayne_ran/article/details/2030915)