前言

三角網格拓樸(Topology)，三角網格拓樸是一種可以用來快速進行搜尋的資料結構，透過預先的整理將網格與網格之間的關係找到並記錄起來，可以有效的提升演算法的運算效率。

三角網格拓樸

在本文中使用到的三角網格拓樸關係有三種，分別是點拓樸關係、邊拓樸關係及面拓樸關係，並在建立之前會將所有點、邊、面都賦予唯一的ID號碼再進行關係的計算，以下將逐一介紹每種拓樸關係。

點拓樸關係

在點的物件內，可以記錄與此點相連的邊線ID以及相鄰的面的ID，也可以再加上紀錄周圍連接的點，但是要記得紀錄的資訊越多就必須消耗更多記憶體去儲存，並且在計算拓樸關係時也需要耗費更多的時間。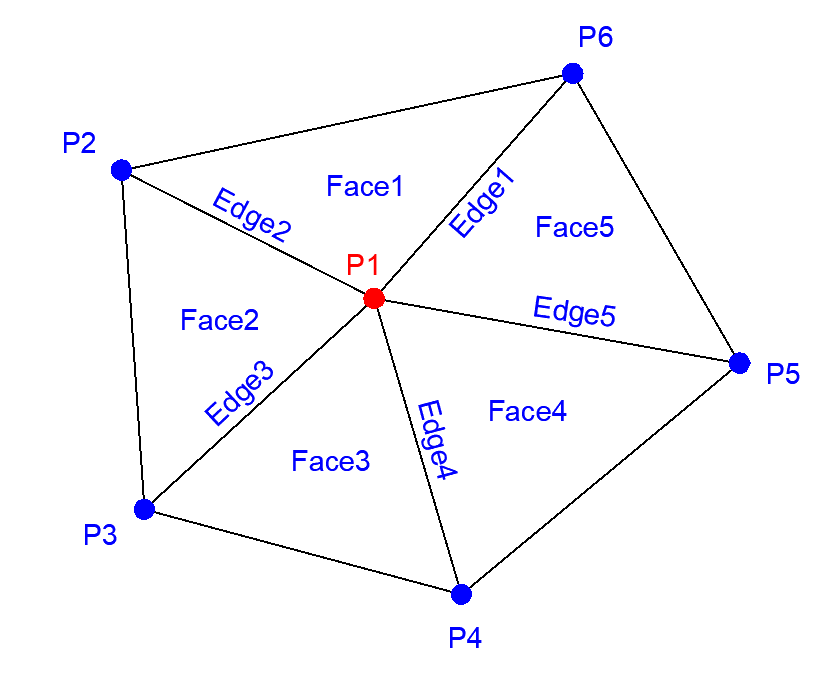

邊拓樸關係

在邊的物件內，可以記錄此邊上的兩點ID，以及與此邊相鄰的兩個面ID，同樣的也可以再將邊與點的關係納入並記錄，視其需求而使用。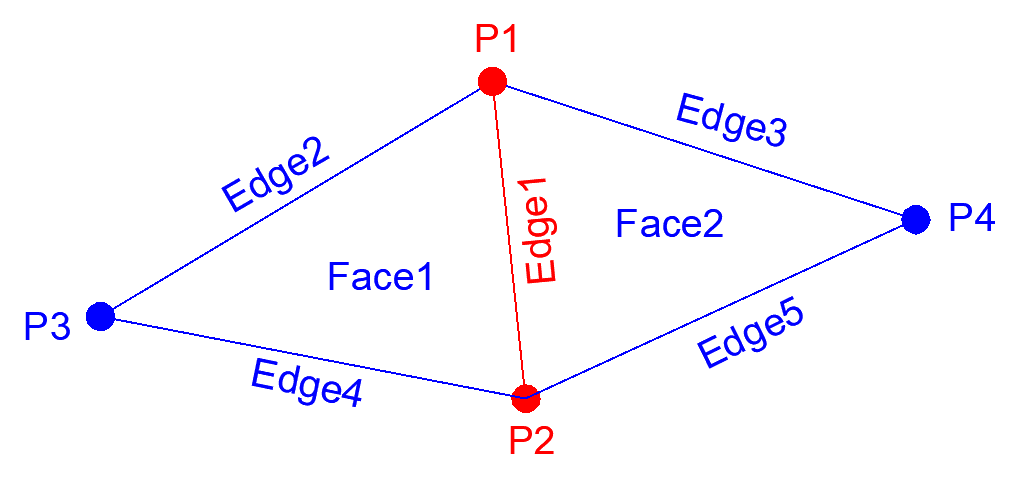

面拓樸關係

在面的物件內，可以記錄面上的點ID與邊ID，以及相鄰的面ID，再一次的面拓樸也能再將更多資訊也記錄進去，但是有沒有別的方法? 可以不要紀錄這麼多嗎?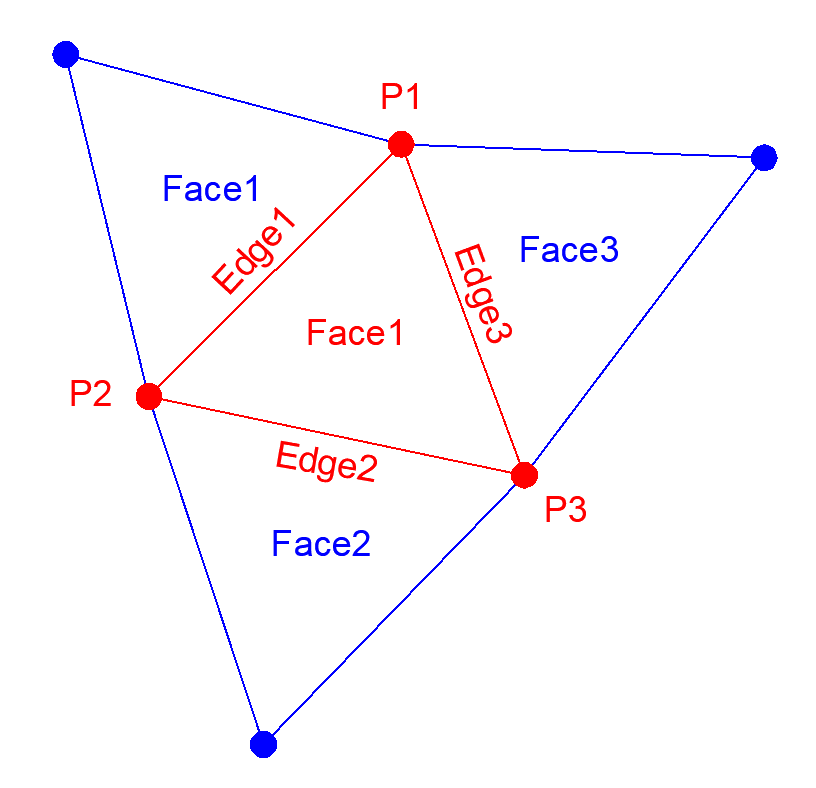

拓樸組合使用

例如我們如果沒有建立面拓樸關係，要找一個面相鄰的面有哪些，這時候我們可以先從該面的三個邊ID，分別對三個邊ID使用邊拓樸關係找尋與邊相鄰的兩個面ID，如此一來會找到六個面的ID，接下來只要去掉自己那個面的ID，就可以留下我們要找的相鄰面了。

後記

這回沒有程式碼，我們先說明了拓樸的關係，透過三角網格拓樸可以幫助我們快速的搜尋網格與網格之間的關係性，在CAD軟體設計中的網格編輯功能，就是透過拓樸關係快速地尋找與修改每片網格的空間資訊，好好善用拓樸關係可以讓軟體的計算速度得到大幅的提升。