今天開始幾天來講幾個應用電路的小範例，讓大家練習一下前幾天學習的成果，首先今天來做一個33的矩陣乘法，矩陣運算在圖形運算中是非常重要的環節，像是GPU等等，所以一個簡單的矩陣相乘也有不同的做法，雖然結果一樣，但使用的資源及速度就會有差，先來看一般大家的做法．

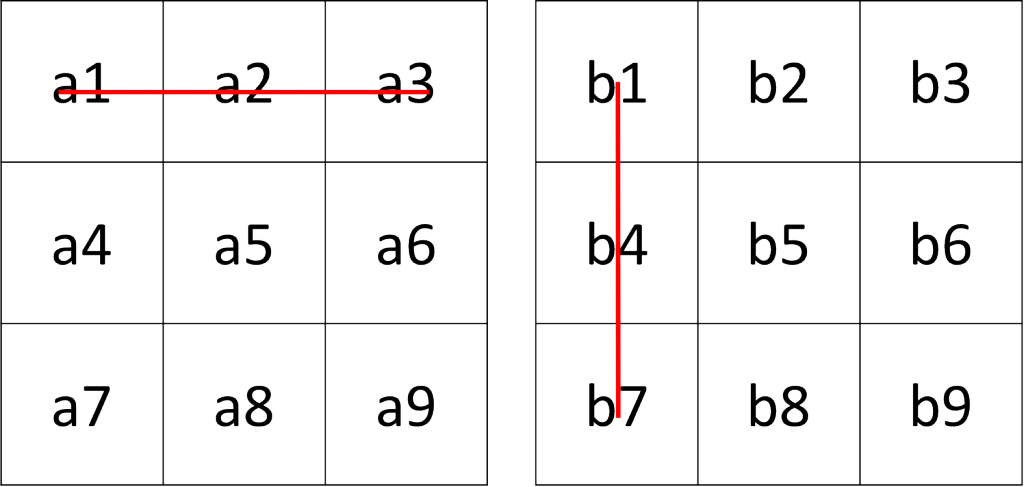
所以我們再算矩陣乘法時，
c1 = (a1b1) + (a2b4) + (a3b7)
c2 = (a1b2) + (a2b5) + (a3b8)
.
.
.
.
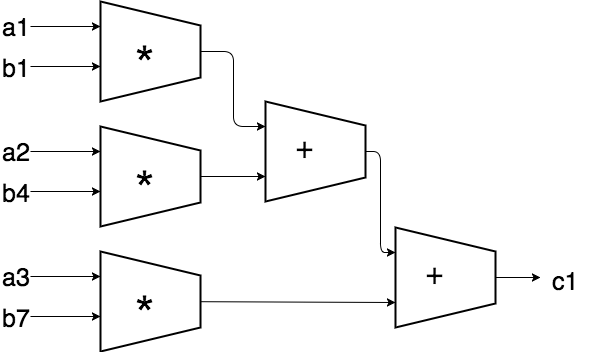
之前常說，在寫verilog時心中要有張電路圖，這邊來看的話，我們一個單位時間能算一個輸出，就像c1 = (a1b1) + (a2b4) + (a3b7)，所以我們需要九個單位時間算完一個33矩陣，然後花了三個n-bit乘法器以及兩個n-bit加法器．

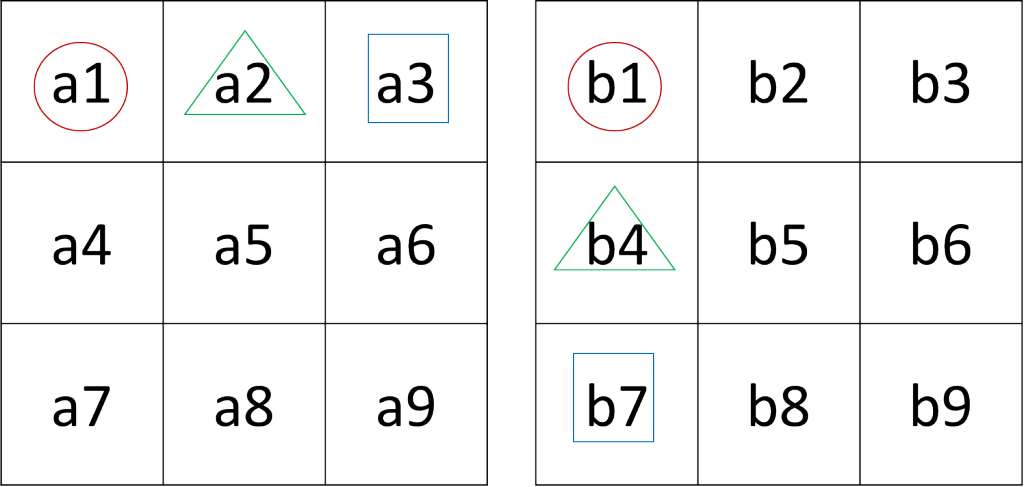
但假設說在資源有限的情況下，要怎麼實作這個33的矩陣乘法呢，我們可以只用一個加法器跟一個乘法器來實作，比較好的寫法還是利用FSM來控制，再算一個row乘以一個colum時，我們拆成三個cycle來運算，
c1 = (a1b1) + (a2b4) + (a3b7)，每相乘一次就做累加，相乘三次並做完累加後就完成一個值的運算，如下：

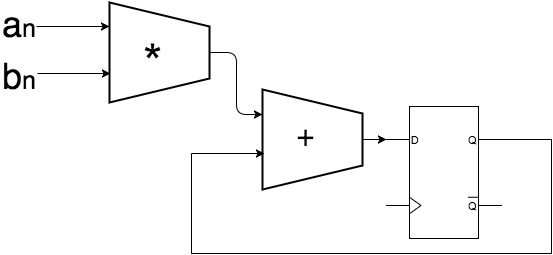
當然你也可以使用更多的資源更快的算完，就把全部的乘法加法攤開就能在一個cycle算完，所以在做電路前不仿先考慮一下，要做一個快速的電路，還是資源小的電路，或著是折衷中的做法，畢竟魚與熊掌不能兼得，所以開始寫verilog之前先好好思考做法吧．